Title: Hidden Worlds: Dynamical Architecture Predictions of Undetected Planets in Multi-planet Systems and Applications to TESS Systems

Authors: Jeremy Dietrich and Dániel Apai

First Author’s Institution: Department of Astronomy, The University of Arizona, Tucson

Status: Submitted to AJ, open access on arXiv

Fans and writers of science fiction alike spend countless hours crafting intricate star systems, replete with planets, moons, and a menagerie of space-faring civilisations. The success of missions such as the Kepler Space Telescope (hereafter Kepler) and the Transiting Exoplanet Survey Satellite (TESS) have shown that our solar system is just one of many multi-planet systems present throughout the Milky Way. However, our ability to accurately determine the “planetary architecture” (the orbital configuration of the planets) of a given extrasolar system is severely lacking. Knowing how planets are configured in different extrasolar systems would greatly aid our understanding of how planets form, and how planetary systems evolve (e.g. via planetary migration). Exoplanets are inherently difficult to detect. The primary means of detecting them involves measuring the tiny dimming of a star as a planet moves in front of it. To better understand stellar systems, instead of considering each exoplanet individually, we can consider the entire population of exoplanets at once through statistical inference. This method has only recently become viable thanks to the wealth of data from modern exoplanet surveys. Today’s paper presents a statistical framework – DYNAmical Multi-planet Injection TEster (DYNAMITE) – designed to predict the presence of exoplanets that have so far eluded detection.

Fire in the Hole!

The core method at the heart of DYNAMITE is to determine the likelihood of finding an additional planet in an existing multi-planet system, based on the overall statistics of an existing representative population. The authors consider a combined probability density function (PDF) over the inclination, orbital period and planetary radius, with the key assumption being that each of these parameters has its own independent distribution. Each of these initial PDFs were based on data from Kepler, with the range of orbital periods restricted from 0.5 to 730 days, planetary radii from 0.5 to 5 Earth radii and inclinations between 0 and 180 degrees. Monte Carlo methods (means of approximating something through repeated random sampling) are then used to sample the full probability distributions and “inject” new planets into the system. In order to come up with sensible results, the planetary system must be dynamically stable. This stability depends on the orbits of the innermost and outermost planets, their masses, and the mass of the parent star. It is difficult to accurately determine the masses of exoplanets via the common transit method, so the authors make use of a mass-radius relation to estimate the masses from the planetary radii.

Sweet Spot

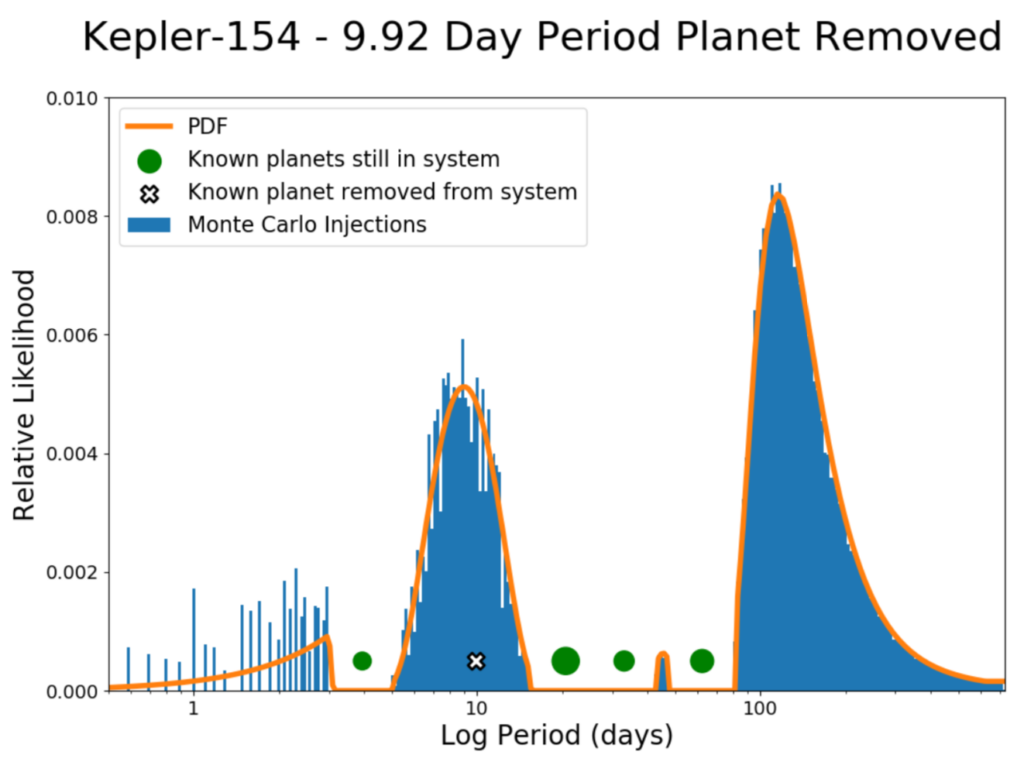
The model underwent rigorous testing for sensitivity and robustness. Several test scenarios included removing a known planet to see if the model could reproduce it, and removing a planet whilst altering the remaining planets. Figure 1 shows an example of the PDF as a function of orbital period for the Kepler-154 system with the known planet at P = 9.92 days (Kepler-154 f) removed. Of the total Monte Carlo predictions that inject a new planet inside the orbit of the outermost planet, 97% correspond to the region of the removed planet. As for the radius, 67% of the models predictions lie within 3 standard errors, while the spread is more substantial for the inclination (43%). The mean injections match the known planet’s parameters quite well (as in Figure 1 where the peak is just below the known value for the period), but the authors nevertheless state that since DYNAMITE is primarily aimed at helping guide future observations, it is not designed to provide exact predictions but rather a likely range of values.

Speculative Execution

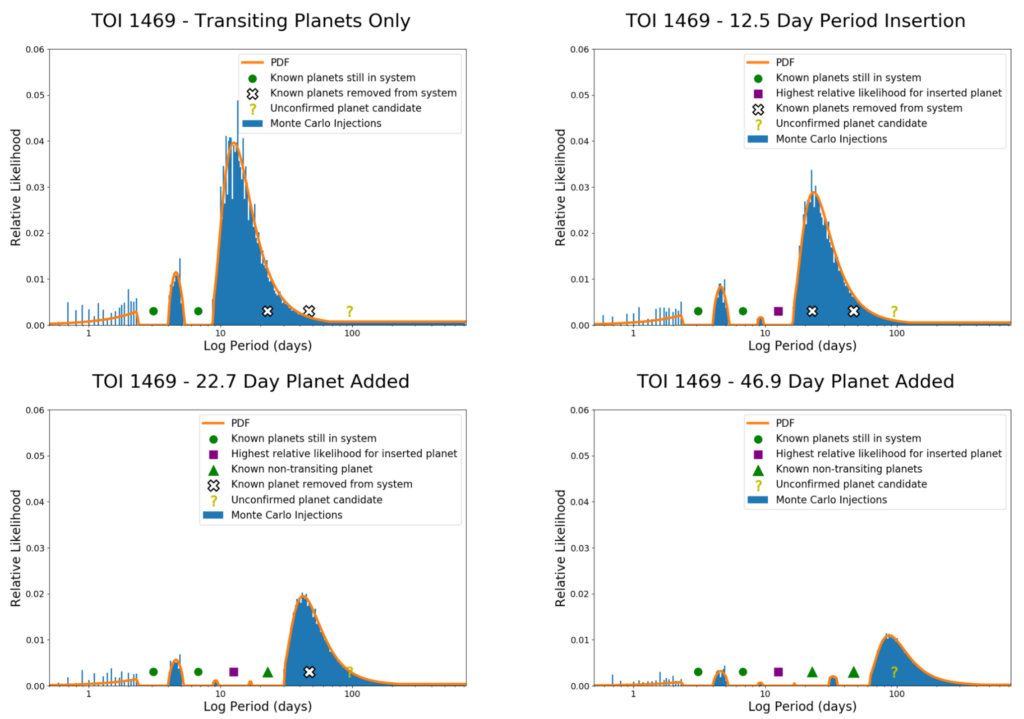
One of DYNAMITE’s major applications lies in the analysis of systems with candidate planets; planets that are suspected to be there but have not yet been definitively confirmed. TOI 1469 is used as an example to illustrate the iterative nature of the statistical model. Figure 2 shows the various stages of DYNAMITE for the TOI 1469 (HD 219134 / Gliese 892) system. This system is known to have two transiting planets, with at least three non-transiting planets. Starting with only the two known transiting planets, the PDF peaks at around 12.5 days. A planet is inserted here, and the model is run again. Now the PDF peaks near the known planet at around 23 days (HD 219134 f has a period of 22.72 +/- 0.02 days), so we insert another planet here and execute the model again. Proceeding in this manner, the model predicts another planet at ~46 days (corresponding to HD 219134 f with orbital period 46.86 +/- 0.03 days), while in the last iteration the model predicts a fourth planet at ~87 days, corresponding to the unconfirmed candidate planet.

To Probability Space and Beyond

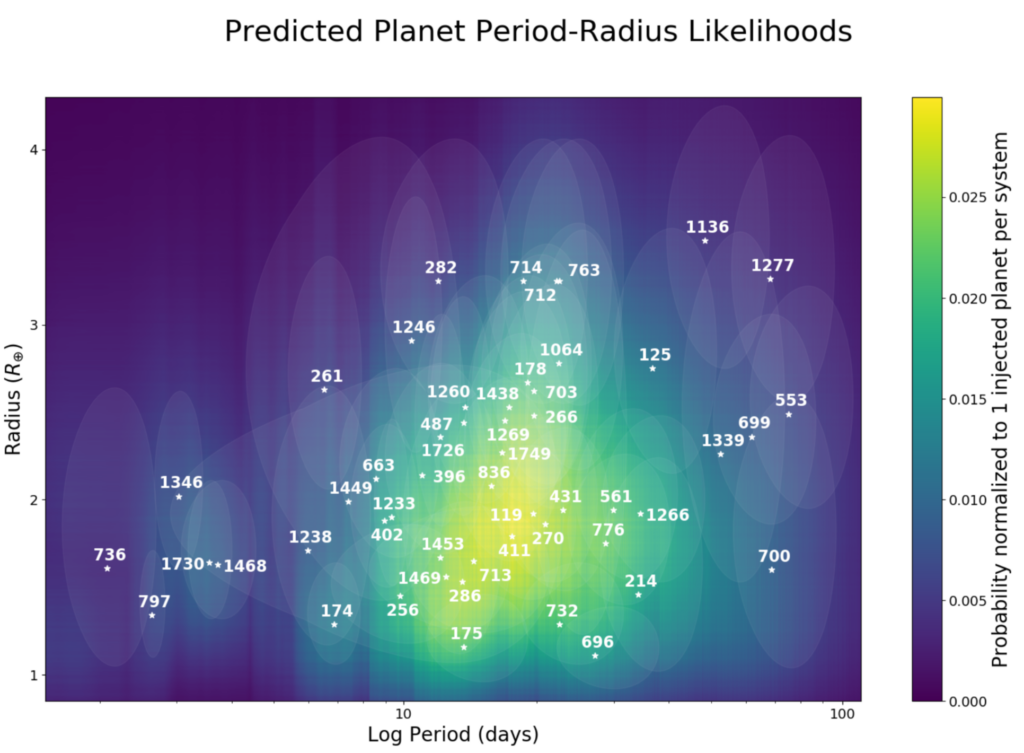
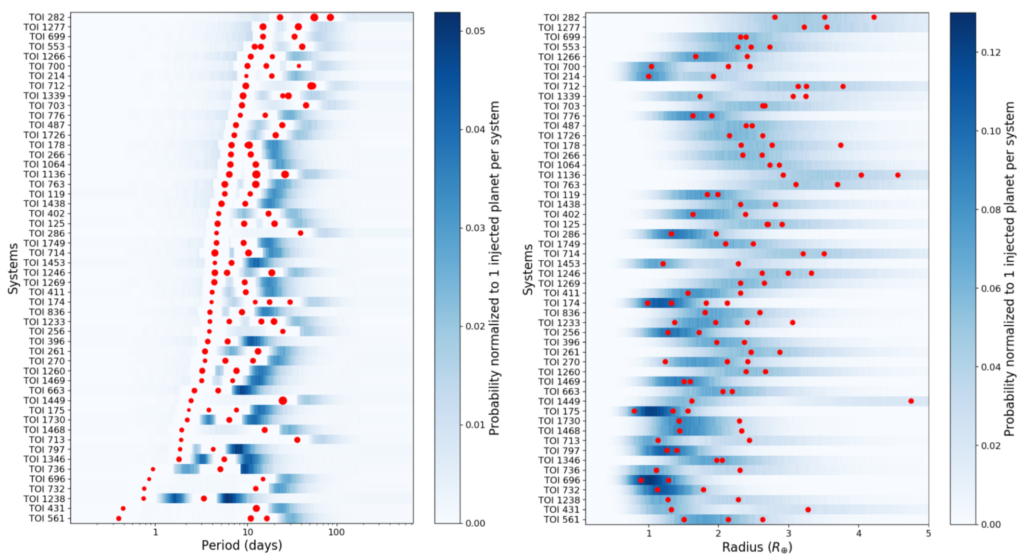
Another purpose of DYNAMITE is to analyse the newly identified multi-stellar systems discovered by TESS and identify the systems most likely to contain additional planets so that they can be surveyed again. A sample of known multi-stellar systems from the ExoFOP-TESS archive was tested with the statistical model. Figure 3 shows the overall results of the model using the period ratio model from Kepler, while Figure 4 shows the exact PDF for each TESS system for the orbital period and planetary radius.

With the ability to predict the locations of hitherto undetected planets, future surveys can be more focused and targeted. Studying these systems in detail, and confirming whether or not these additional planets are present, allows us to constrain and refine models of planetary architectures, our knowledge of the mechanisms that govern the evolution of planetary systems, and, ultimately, our understanding of how exoplanets form.

• About the Author

About Mitchell Cavanagh

Mitchell is a PhD student in astrophysics at the University of Western Australia. His research is focused on the applications of machine learning to the study of galaxy formation and evolution. Outside of research, he is an avid bookworm and enjoys gaming, languages and code jams.

Related posts:

Exomoons disguised as aliens The Singles’ Club Choosing targets with TESS Darwin’s Theory of Evolution, but make it planets