Authors: James R. Beattie, Christoph Federrath, Ralf S. Klessen, and Nicola Schneider
First Author’s Institution: Research School of Astronomy and Astrophysics, Australian National University, Canberra, ACT 2611, Australia
Status: Published in MNRAS [closed access], available on arXiv.
Turbulence is messy. The chaotic, seemingly random motions of gas, described broadly by the term turbulence may be more familiar when jostling people around in an airplane, but they also have major implications for the conditions for star formation. Turbulence’s effects can, in some cases, prevent significant amounts of gas from becoming gravitationally bound, making it harder for star formation to occur. In other cases, turbulence might help to compress gas to higher densities and drive the formation of new stars.
Quantifying astrophysical turbulence in an interstellar gas cloud is particularly difficult. This is commonly done by measuring statistical properties of the gas’s velocity. The Mach number describes how fast the local gas is typically flowing relative to the fluid’s sound speed, and is used as an ingredient in many turbulence-dependent theories of star formation.
Today’s paper develops a new way of measuring the Mach number of a cloud without actually knowing anything about the velocity of the gas. Instead, this method uses only the density distribution of the cloud! This approach can not only be used to bolster the reliability of velocity-based measurements of turbulence properties with an independent point of comparison, but perhaps also to determine Mach numbers for interstellar gas structures where the velocity might be too confusing or difficult to measure. It all revolves around a trick using a quantity known as the fractal dimension.
The Fractal Dimension
Fractals are systems that have self-similarity across physical scales. Besides looking extremely cool and possessing fascinating mathematical properties, they can also be useful for describing the interstellar medium, the stuff found between stars! The fractal dimension is a number that quantifies how completely something (like a molecular gas cloud, for instance) fills up 3D space. A perfectly distributed cloud of constant density would have a fractal dimension of 3, whereas a perfectly thin filament of matter would have a fractal dimension of 1, and a flat sheet would have a fractal dimension of 2. It turns out that star-forming clouds tend to be largely made up of filaments and sheets of matter (so-called “shocks”), so we can expect their fractal dimensions to be between 1 (like a filament) and 2 (like a sheet).
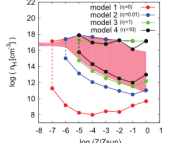
There are lots of ways to measure this fractal dimension, but the one used by the authors of this work is to consider the mass-length scaling relation. According to this relation, if you look at the amount of mass found in observed clouds, there’s a scaling relationship which says how much mass is contained within a region of a given size.
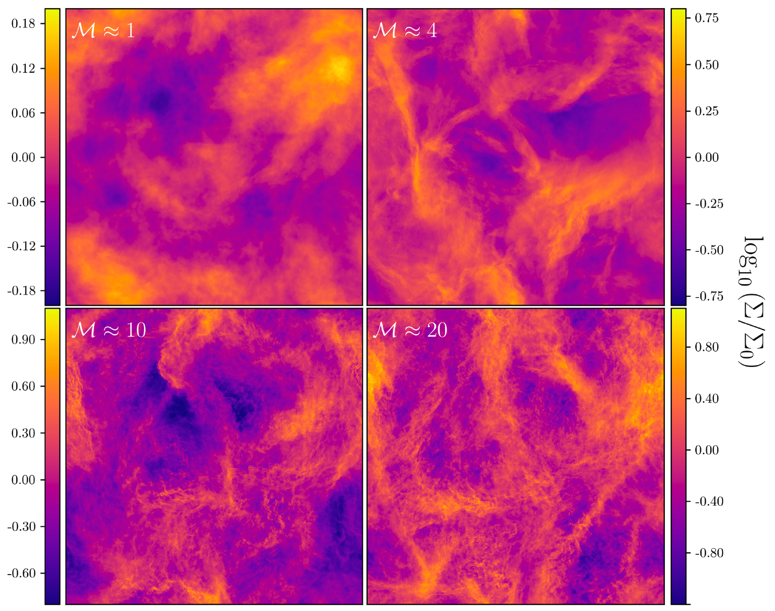
The authors run hydrodynamic simulations of a bunch of gas clouds with different strengths of turbulence (and therefore different Mach numbers), and see that the fractal dimension of these clouds actually depends on the Mach number! You can see the difference in the complexity of the density structures created in these simulations in Figure 1. This means that, by fitting an equation to the relationship between Mach number and fractal dimension, they can find the Mach number using a measurement of the fractal dimension, without even using a measurement of gas velocities.
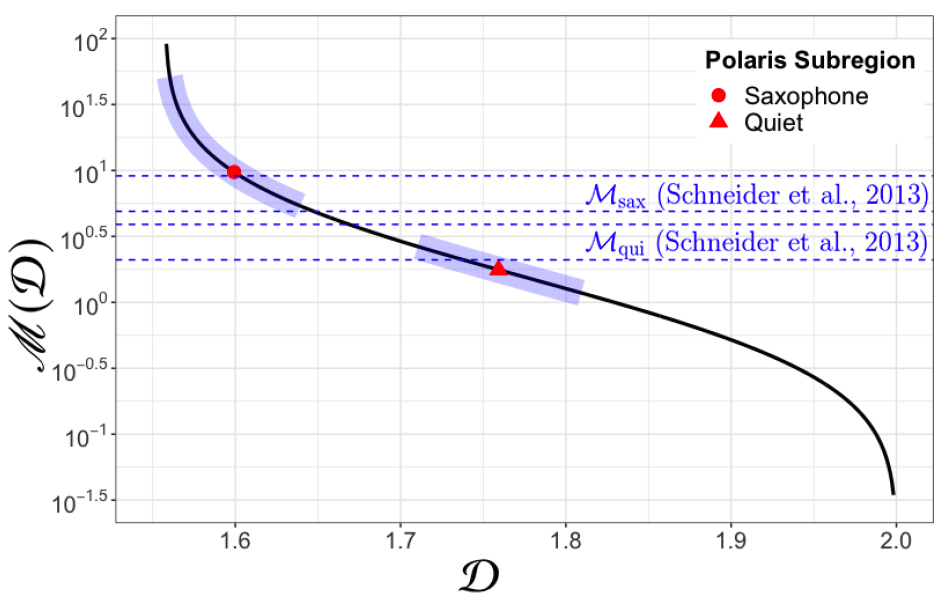
To show that their method works, the authors look to observations of two very different molecular clouds in the Polaris Flare region, a region of space full of filamentary gas structures, where the Mach numbers have been measured using more traditional methods. The comparison is shown in Figure 2. Lo and behold, the new method produces results that agree with the previous measurements, though there is a lot of uncertainty in the high-Mach number limit. This means their method may be less reliable for regions with particularly high-velocity gas flows. Even so, developing another reliable way to measure the turbulent properties of clouds is an extremely valuable step in unraveling the complex web of physics that governs the star formation process.
Astrobite edited by Catherine Clark and Haley Wahl.
Featured image credit: modified from Figure 4 of the paper.