Authors: The LIGO Scientific Collaboration, the Virgo Collaboration and the KAGRA Collaboration
Status: Available on the arXiv
Over the last few decades, astronomers have opened up new windows into the universe, allowing us to study the cosmos not only with light, but also with other messengers, like neutrinos and gravitational waves (GWs). Specifically, the last few years have witnessed a deluge of gravitational wave detections. The first detection of a black hole merger was just six years ago, but today there are over 50 confirmed binary merger detections.
The Gravitational Wave Background
The first detected GW signals have all been from compact binary coalescences (CBCs), where two massive objects such as neutron stars or black holes merge and emit gravitational waves. These signals, which last a few seconds, have frequencies that are in the same range as those which the human ear can detect. Although any merger in the universe produces these GWs, in order to detect them we need the merger to be very close, which, astrophysically speaking, means less than a few tens of millions of light years. Otherwise the GW amplitude will not be large enough to be observed by current detectors.
However, all of the distant coalescences, in addition to some other sources of GWs across various frequency bands — core collapse supernovae, rotating neutron stars, cosmic strings, primordial black holes — can still add up to make a ubiquitous sea of GWs. This discordant hum of individually undetectable GWs makes up what we call the “Gravitational Wave Background,” or the GWB. The authors of today’s paper set out to see if the GWB is detectable in current GW detector data.
Searching for the GWB
The GWB is, by definition, made up of undetectable (by current standards) signals. Because these signals add up randomly, or “stochastically,” the GWB is notoriously hard to detect. In order to see if there is any evidence for the GWB in current data, the authors look at the cross-correlation of different detectors. Although the GWB might be below detection thresholds or appear as noise in one detector, weak but correlated signals in various detectors can add up to a detectable signal when combined. This cross-correlation technique has been used in previous searches for the GWB (for astrobites coverage of these previous searches, check out here and here). However, previous analyses, as well as today’s paper, have come up short. As of now, there is no significant detection of the GWB. The results of the search are summarized in Figure 1.
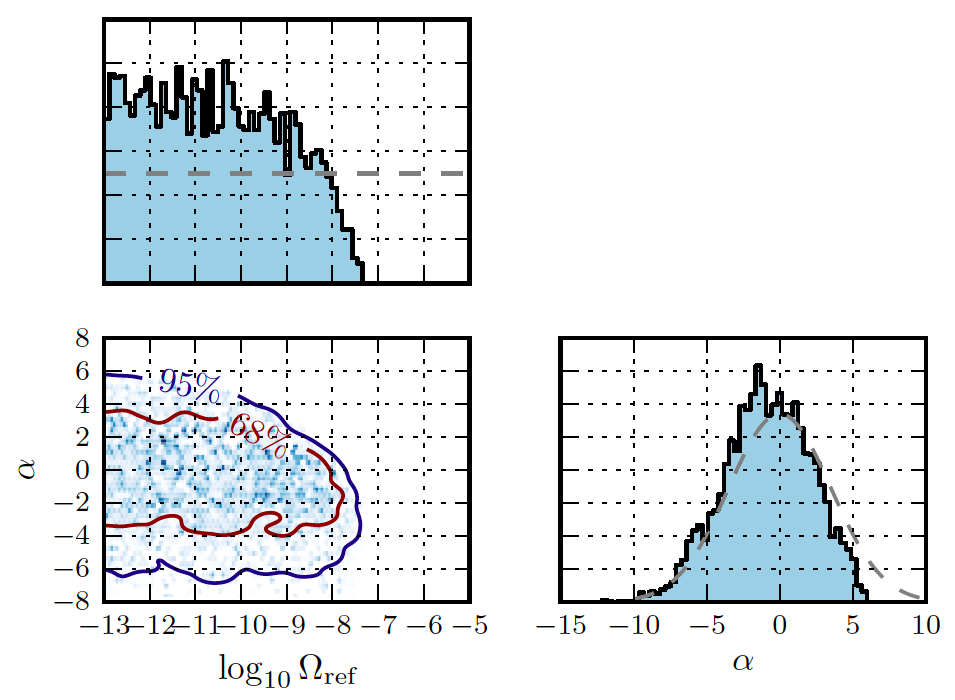
Figure 1: the probability distributions of the amplitude of the GWB (
The backgrounds to “The Background”
One of the difficulties in this analysis is that the GWB is not the only thing that can create correlated noise in GW detectors. One of the more interesting challenges is that some parts of the GW detectors rely on the use of magnets. Sometimes, because of a bizarre phenomenon called “Schumann resonances,” occurrences in Earth’s ionosphere can cause changes that affect magnets on a global scale, which could, if not treated carefully, appear as a correlated signal. The analysis also uses some novel techniques to eliminate “glitches” in their data to optimize the sensitivity of the analysis. After accounting for all of these backgrounds, the authors still find no evidence for the GWB. Figure 2 compares the limits that can be placed because of this non-detection with estimates of the GWB strength as a function of frequency.
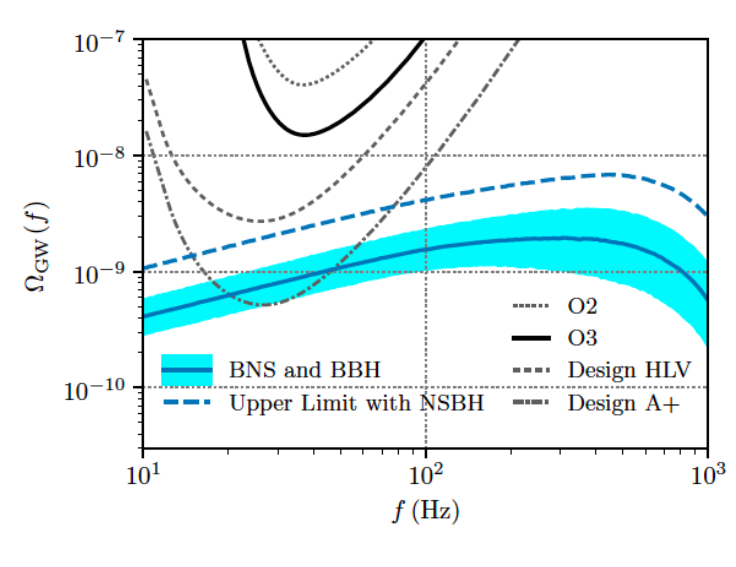
Figure 2. Predictions of the GWB strength are shown in blue and compared to the limits placed by this analysis in solid black. The dashed blue includes contributions from mergers of neutron stars with black holes, but no confirmed detections of these mergers have been made to date, so there is significant uncertainty on their rate. Future improvements to detectors (dashed and dash-dotted gray) should allow future searches to be sensitive to the GWB. Figure 5b from today’s paper.
Combining results
Although the authors of today’s paper don’t find evidence for the GWB, their results are still extremely interesting. The results place a limit on the number of binary black hole mergers in the distant universe. However, LIGO and Virgo have detected plenty of mergers of compact objects in the nearby universe. Thus, if one wants to make a prediction about how many, say, black hole mergers, there are in the entire universe, you have to predict enough mergers to agree with the fact that some have been detected, but not too many such that you overshoot the bounds from the GWB analysis. The result of combining these results and making a prediction of the rate of binary black hole mergers is shown in Figure 3.
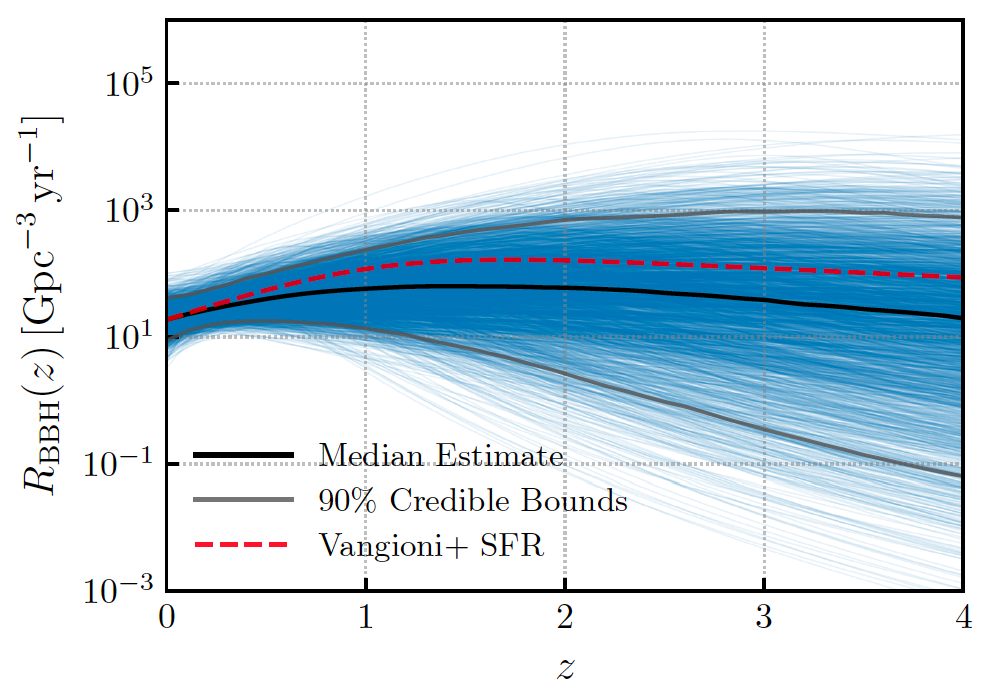
Figure 3: the constraints on the rate of binary black hole mergers as a function of redshift, z. The blue lines each show a different simulated result, and the median of these results is shown in black. These experimental results agree well with a model shown in the red dashed line. Figure 6 from today’s paper.
Despite the fact that the authors were unable to claim a detection of the GWB, the analysis was still a major step forward. The analysis combined a variety of novel techniques that drastically improved the sensitivity of the analysis when compared to previous searches. These new techniques, as well as the improved sensitivity that will come with future detectors, could be the key to detecting the elusive GWB.
Astrobite edited by Jamie Sullivan
Featured image credit: LIGO Scientific Collaboration
