Title: Bayesian analysis of Enceladus’s plume data to assess methanogenesis
Authors: Antonin Affholder, François Guyot, Boris Sauterey, Régis Ferrière & Stéphane Mazevet
First Author’s Institution: Institut de Biologie de l’École Normale Supérieure, ENS, Université Paris Sciences et Lettres, Paris, France; Institut de Mécanique Céleste et de Calcul des Éphémérides, Observatoire de Paris, Université Paris Sciences et Lettres, Paris, France
Status: Published in Nature Astronomy [closed access]
Enceladus: A prime astrobiology target
One of the highlights of the prolific Cassini mission to the Saturnian system was the detection of methane and molecular hydrogen, among other trace gases, in a plume of Enceladus’ ocean material ejected into space (see here and here). A leading hypothesis for the presence of H2 in the plume points to hydrothermal activity at the base of the Enceladus’ subsurface ocean. If the origin of gases detected in the plume is indeed in hydrothermal vents, these gases can tell us about the environment of these deep sea vents. If the hydrothermal activity on Enceladus resembles that of the Earth, then both H2 and CH4 can be produced in the vents; H2 can be produced through serpentinization in the rocky core of Enceladus, while CH4 can be produced through a reaction of carbon dioxide (CO2) and H2. Hydrothermal vents can also support biological origins of methane: hydrogenotrophic methanogens (life that feeds on hydrogen and produces methane) exist near hydrothermal vents on Earth, and derive their energy from converting H2 and CO2 (or other forms of dissolved carbon) to CH4.
While previous works have taken both a theoretical and an experimental look at the viability of methanogenesis (production of methane by biology) in deep-sea Enceladus like environments, the current work goes one step further and tries to quantify the probability that biological methanogenesis might explain the measurements made by Cassini of Enceladus’ plume. The authors also employ a Bayesian framework, which allows one to calculate the probability of different scenarios (e.g., presence v/s absence of biology) and hence enables a rigorous comparison.
Modelling the production of gases in a Bayesian framework
In general, the Bayesian approach aims to quantify the probability that alternate hypotheses are true given actual observations. By translating the different hypotheses into mathematical models, simulations can be used to find the likelihoods of the data occurring under the alternate scenarios. A priori (prior) knowledge of factors that influence the probability of each hypothesis being true, including previous observations, is combined with the likelihoods to give the a posteriori (posterior) probability of each hypothesis being true. Figure 1 shows the Bayes equation used in this work. The observables (or the data) considered here are the escape rates of H2 (φH2) and CH4 (φCH4), and the H2/CH4 ratio, which were measured by Cassini.
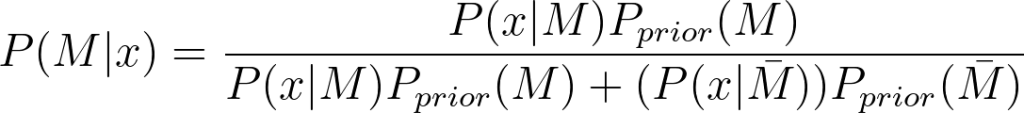
The authors use a general model that can simulate both the hydrothermal conditions near a vent and the chemistry due to biological methanogenesis, and calculate the gases being produced. The model takes the composition and temperature of the hydrothermal fluid, and the composition of the ocean, as inputs. Under the assumption that the escape rate of gases being produced near the hydrothermal vent is equal to the scape rate of gases being lost in the plumes, the total CH4 and H2 escape rates (φH2 and φCH4), and the H2/CH4 ratio can be calculated from the model.
Results
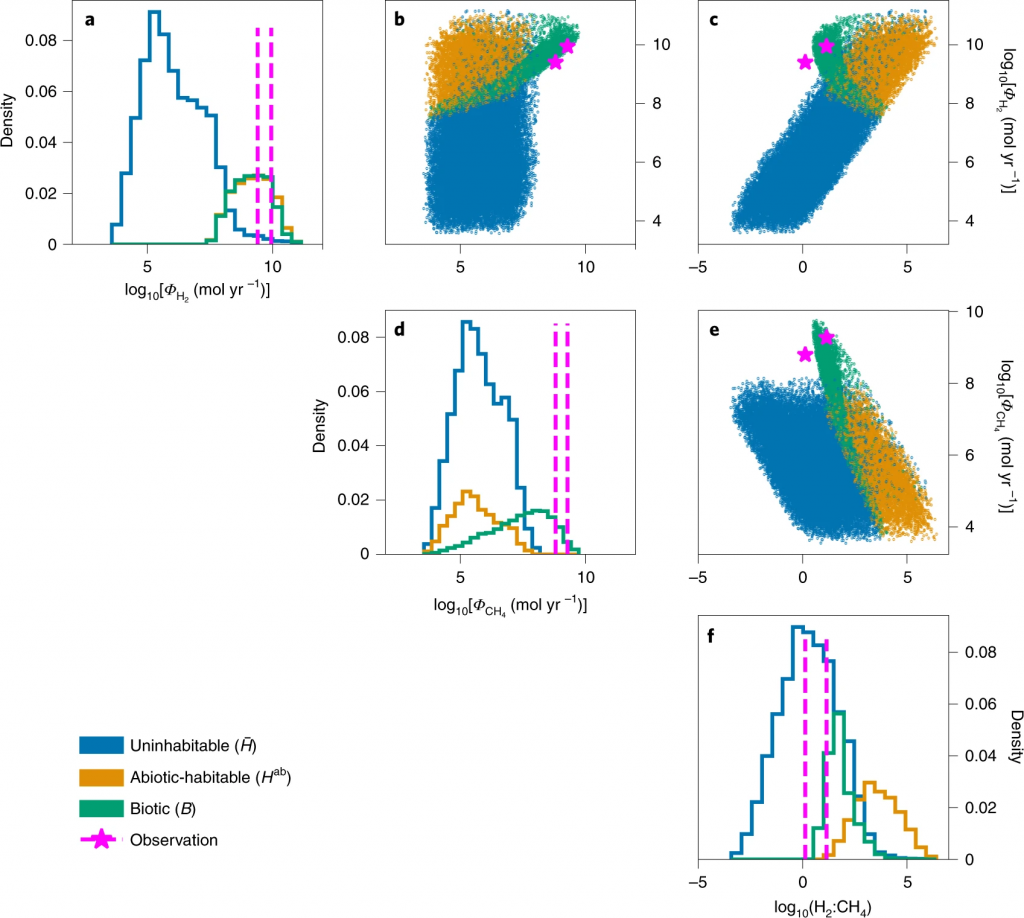
Firstly, the authors set out to explore how the observables (φH2 , φCH4 and H2/CH4) produced from their model compared to the Cassini observations. They run a set of 50,000 simulations using random values of the model parameters drawn from their prior distributions (see Extended Data Figure 3 in the paper). In about 32% of these simulations, the random set of parameters allowed the modelled population of methanogens to grow, while in the remaining 68% were methanogens could not grow. The habitable subset was evenly split at random into two subsets of 8,008 simulations. In one subset, methanogenesis was not simulated, whereas methanogenesis coupled with the geochemical model was simulated in the second subset. The simulated distribution of the observables, and their comparison to the actual data, are shown in Figure 2. The key take-aways from this analysis are:
- Simulations corresponding to the case where biological methanogenesis is included consistently explain the observed rates of CH4 and H2 and the ratio of H2:CH4.
- Simulations in which CH4 only originates via abiotic reactions cannot explain all observations.
- Especially for CH4, the observed escape rate lies far from what could be expected from the abiotic conversion of H2 and CO2 through serpentinization. In contrast, it falls in the range of expected values when biological methanogenesis is occurring.
The authors also evaluate the posterior probabilities of the habitable scenarios, with and without methanogenesis, using the Bayes formula in Figure 1. They explore a range of values for the prior probability of methanogenesis (as we don’t know much about this probability) and evaluate its effect on the posterior probability that methanogenesis occurs, given the Cassini data. They find that the posterior probability of methanogenesis is the highest provided that the prior probability of methanogenesis, given habitable conditions, exceeds a threshold of around 0.35 (see Figure 3 in the paper). If this prior probability is low, the Cassini measurements are consistent with habitable yet uninhabited hydrothermal vents.
Future work and exciting prospects
The authors highlight that better constraining the age and duration of temperature conditions conducive to the emergence of life near deep-sea vents in Enceladus should help define ranges of credible values for the prior probability of biological methanogenesis, in the presence of habitable conditions. They also emphasize that while this work only considers serpentinization as the source of abiotic methane, there might be other processes generating methane, like ‘leaching’ of primordial methane accumulated in the core when Enceladus formed. Isotopic measurements such as the 14N and 15N ratios of NH3, as well as the 13C to 12C and deuterium-to-hydrogen ratios of CH4, might shed new light on the nature of Enceladus’s core and the origin (primordial or modern) of methane. Proposed Enceladus missions like ELF and observations from JWST of plumes on other ocean worlds like Europa can potentially identify abiotic sources of methane that might explain the Cassini observations without calling for methanogenesis.
Astrobite edited by Ryan Golant
Featured image credit: NASA-GSFC/SVS/NASA/JPL-Caltech/Southwest Research Institute




Thank you. I am fascinated by Enceladus.
Glad you liked it! Enceladus is indeed very fascinating.