Paper: Detecting stochastic gravitational waves with binary resonance, Bridging the μHz Gap in the Gravitational-Wave Landscape with Binary Resonances
Authors: Diego Blas and Alexander C. Jenkins
Author Institutions: Departament de Física, Universitat Autònoma de Barcelona; Institut de Fisica d’Altes Energies (IFAE) The Barcelona Institute of Science and Technology; Theoretical Particle Physics and Cosmology Group, Physics Department, King’s College London
Status: Published in Phys. Rev. D., Phys. Rev. Lett. (respectively) [closed access]
Gravitational waves of various frequencies, amplitudes, and forms are produced by a wide range of astrophysical and cosmological phenomena. Not only can they carry information about massive astrophysical objects, such as the colliding black holes and neutron stars detected by the LIGO–VIRGO Collaboration, gravitational waves can also radiate signals from other physical processes in the universe. One particularly exciting signal is that of a stochastic gravitational wave background, an incoherent sum of signals from unresolved sources. Such a background may be created by a combination of astrophysical sources, such as a population of super massive black hole binaries, and cosmological events such as inflation, early-universe phase transitions, and the decay of cosmic strings. Each phenomenon has a frequency range over which we expect to see its signal. Observing the list of possible phenomena requires a range of gravitational wave detectors sensitive to different frequency bands. This is analogous to the range of telescopes built to span the electromagnetic spectrum, from arrays of radio dishes to gamma-ray observatories in space, which combine to give us a better understanding of a wide range of phenomena in the universe.
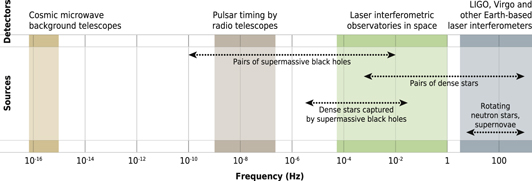
Current and planned gravitational wave experiments cover a wide range of frequencies on the order of nanohertz to tens of kilohertz. However, there are gaps in the frequency ranges covered, most notably in the microhertz (10-6 Hz) region, between the sensitivities of pulsar timing arrays and future space-based interferometers like LISA, as shown in Figure 1. The authors of today’s featured paper propose a technique with the potential to bridge this gap.
Why the gap?
Given the impressive list of ongoing and planned gravitational wave detectors, you might wonder about the uncovered band. First, one should understand what determines the frequency bandwidth for a gravitational wave detector. In the case of pulsar timing arrays, in which radio telescopes monitor changes in the timing of signals received from millisecond pulsars due to the passage of gravitational waves, the frequency sensitivity is set by the sampling properties of the data. The upper limit comes from the time between measurements–observations are performed on the order of weeks (T~weeks), corresponding to hundreds of nanohertz (f=1/T) – and the lower limit from the total observation time (on the order of nanohertz for observatories operating on an order of 10 years). Similarly, interferometers are limited by observation time and have even stronger constraints stemming from the sensitivity of the instrument to the size of the gravitational wave signal. For example, the ground-based LIGO-VIRGO observatory covers 10 to 1000 hertz, whereas the space-based LISA observatory, with a planned arm length nearly a million times larger than LIGO’s, will be most sensitive in the range from 0.1 millihertz to 0.1 hertz. Space-based interferometers could be made even larger and more sensitive to signals at even lower frequency (which is inversely proportional to length scale). To detect signals in the microhertz gap, an interferometer would need to be built on astronomical scales, for example on the size of the solar-system. Constructing such an interferometer is a futuristic task at present, hence the gap in the frequency band covered by current and planned detectors.
In today’s paper, the authors propose another possible technique for creating gravitational wave observatories on astronomical scales by exploiting existing astronomical objects rather than building from scratch. They propose using binary systems to detect gravitational waves by considering the gravitational wave-induced oscillations between two freely falling masses in a gravitationally-bound orbit.
Binary response to gravitational waves
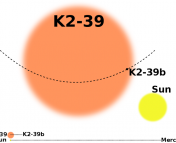
Gravitational wave detectors in general operate by observing how the passage of the waves perturb the spacetime between objects. Like in any other system of masses, the separation of the two bodies in a binary system is stretched and compressed by passing gravitational waves. These interactions leave imprints on the system’s orbit, as shown in Figure 2.

If the gravitational wave frequency is an integer multiple of the binary’s orbital frequency, then the binary responds resonantly to the gravitational waves. Additionally, if the gravitational wave signal lasts longer than the period of the binary, the effects accumulate over time. The combined resonant amplification and accumulation of the signal turns otherwise tiny perturbations into an observable effect.
This technique is especially of interest for a stochastic gravitational wave background since the signal is persistent, allowing the orbital deviations to accumulate. The background can be studied at any frequency using this technique, we just need to measure a binary system with an orbital frequency matching the frequency of interest to meet the resonance requirement. Covering the current gap in the microhertz region requires orbital periods on the order of a month (order 106 seconds, corresponding to a frequency of order 10-6 s-1). The authors propose using the Earth-Moon system, since the Moon orbits Earth with a period of about 28 days.
It turns out that we already have technology in place which would allow us to take the necessary measurements of the Earth-Moon system. The Moon already hosts five ‘retroreflectors’ placed by Apollo astronauts and two unmanned Soviet landers. These retroflectors are designed to reflect light back along the same direction it came from. Measuring the time the light needs to travel between the Moon and Earth reveals the distance between them, given that the speed of light is known. The Earth-Moon distance has actually been measured this way for over fifty years. Today’s paper predicts that if the Earth-Moon distance can be measured to an accuracy of about 0.1 mm, then we may (depending on the signal strength and instrument sensitivity) be able to see fluctuations from a microhertz gravitational wave background. The authors believe that such measurements may be possible with current technology and will help expand our coverage of the gravitational wave sky.
Astrobite edited by Cole Meldorf and Jana Steuer
Featured image credit: NASA