Title: Massive black hole binary systems and the NANOGrav 12.5 year results
Authors: Hannah Middleton, Alberto Sesana, Siyuan Chen, Alberto Vecchio, Walter Del Pozzo, Pablo A. Rosado
First Author’s Institution: School of Physics, University of Melbourne, Parkville, Victoria, Australia
Status: Published in Monthly Notices of the Royal Astronomical Society [closed access]
Imagine that you’re at a coffee shop. There are couples talking to each other at each table. It’s so busy that you can’t make out anyone’s conversation – you can only hear the noisy combination of their voices. Just by measuring the noise in the cafe, what could you learn about the customers?
Actually, a lot. From the volume of the noise, you could estimate the number of couples enjoying a drink. By measuring the power spectral density (the density of the noise’s power per frequency as a function of frequency), you could estimate the number of people with deeper voices compared to higher-pitched voices. That background noise is full of information that you can characterise.
Now imagine that the coffee shop is actually our Universe, and the couples are supermassive black hole binaries with masses greater than a billion suns. Their voices are nanohertz-frequency gravitational waves, and the overall noise in the cafe is the unresolvable combination of waves from every supermassive black hole binary in the universe – the gravitational wave background. And at the centre of it all, you are the gravitational wave background detector. How do you characterise the background, and what do you learn about black holes and galaxy mergers?
Detecting a gravitational wave background
Supermassive black holes lie at the centres of galaxies, and when two galaxies merge, their black holes form a binary. As the black holes orbit around each other, they radiate nanohertz-frequency gravitational waves, causing them to inspiral and eventually merge themselves.
Since gravitational waves are emitted from binaries across the universe, they overlap, forming an incoherent background. If the binary orbits are circular, we expect the background’s power spectral density to follow a power-law which has an amplitude to describe how loud the background is, and a spectral index which parameterises how steeply the noise level drops as frequency increases. The amplitude is dependent on the rate of binary mergers per unit volume and per unit of time.
To measure the background, we use a pulsar timing array. Pulsars are rapidly rotating neutron stars that emit radiation from their magnetic poles. If their radiation beams sweep across the direction of the earth, we detect a radio pulse. These pulses are so reliably regular that we can measure the nanosecond delay in their expected arrival times as gravitational waves in the background stretch and compress the space between the pulsar and the earth.
Recently, the North American Nanohertz Observatory for Gravitational waves (NANOGrav), amongst other pulsar timing arrays, published evidence for a `common noise process’ in their data, but there isn’t enough evidence yet to claim that the signal is a gravitational wave background. But if the signal is from the background, we can begin to study what it tells us about supermassive black hole binaries.
Modelling the noise
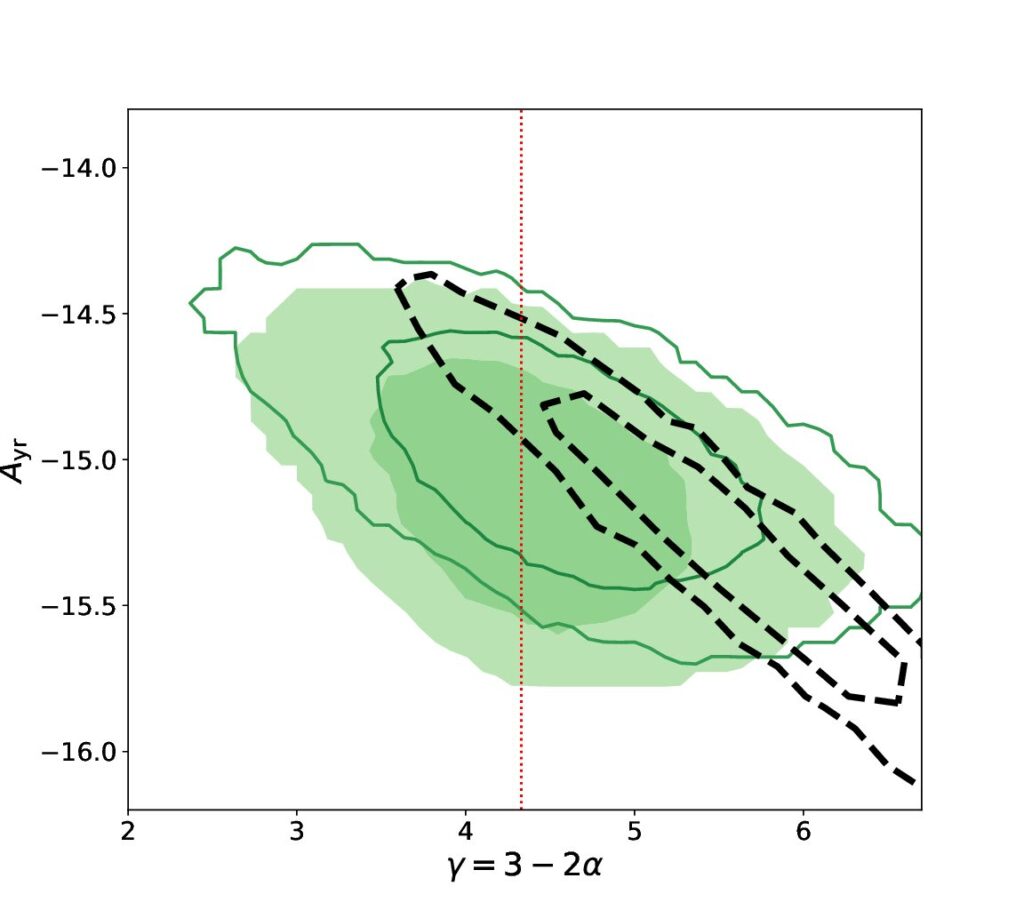
By fitting a power-law to NANOGrav data, the authors recovered a distribution of the most likely amplitudes and spectral indices given the data, shown by the black contours in Figure 1. The results are consistent with simulations, suggesting that the source of the signal might be from a gravitational wave background. Using these results, we find the merger rate to be 10-11 – 2 per Gyr per cubic Mpc.
That is a very unconstrained number, and it doesn’t teach us much about supermassive black hole binaries because the model is too simple. It doesn’t take into account that the binary black holes also interact with surrounding gas and stars, and their orbits are likely eccentric, not circular. If these interactions didn’t happen, the black holes would take too long to merge, and we would see more binaries in the centres of our galaxies instead of a single black hole. We also need to make some assumptions about the mass distribution of supermassive black holes in our universe.
The authors develop two models to compare: a simple mass distribution of supermassive black hole binaries (labelled M16); and a more complicated model that allows for eccentric binary orbits with gas and star interactions (labelled C19). The recovered merger rate is significantly more constrained with these two models (see Figure 2). The C19 model is particularly effective at constraining the merger rate, giving a value of 1×10-5 to 5×10−4 per Gyr per cubic Mpc (green outline in Figure 2).
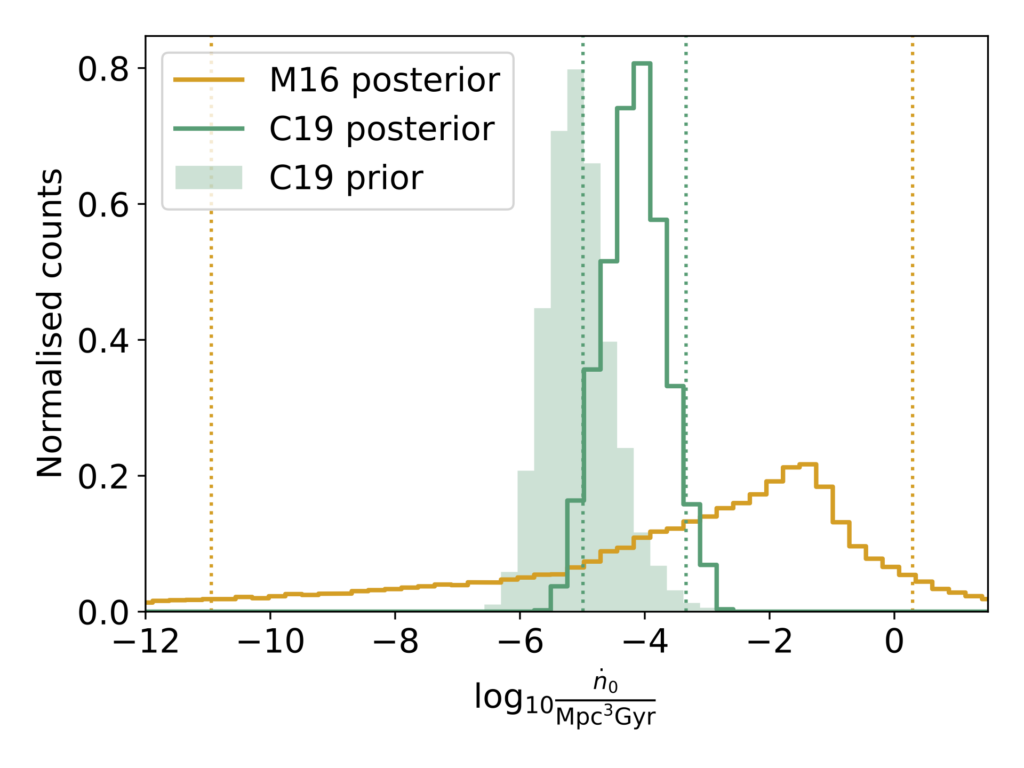
Therefore, assuming that the signal is from a gravitational wave background, we can begin to estimate the merger rate of supermassive black holes in the universe. With more data in the future, we can make more informed analyses to learn even more about galaxy mergers. Astronomers had better get some more coffee…
Astrobite edited by Katherine Lee and Catherine Clark
Featured image credit: Nolan Issac