About Rohit Chandramouli
University of Illinois at Urbana-Champaign
Rohit is a 5th-year Ph.D. candidate at the University of Illinois at Urbana-Champaign, working on gravitational wave physics and astronomy. He focuses on modeling gravitational waves from hierarchical triple systems for space-based detectors like LISA, as well as investigating systematic bias arising from mismodeling waveforms. In his free time, Rohit enjoys cooking, watching TV, reading, and drawing..
Paper title: Nonlinearities in black hole ringdowns
Authors: Keefe Mitman, Macarena Lagos, Leo C. Stein, Sizheng Ma, Lam Hui, Yanbei Chen, Nils Deppe, François Hébert, Lawrence E. Kidder, Jordan Moxon, Mark A. Scheel, Saul A. Teukolsky, William Throwe, and Nils L. Vu
Status: arXiv open access, accepted at PRL
Merger-Ringdown of Binary Black Hole Coalescence
Gravitational waves formed by binary black hole mergers allow us to probe gravity on the strongest of scales. The merging of black holes is described in this bite, but the key message is that it consists of three acts – 1) the inspiral, where the two black holes dance around each other in orbit, 2) the merger, where the two black holes merge into one (remnant) black hole, 3) the ringdown, where the remnant black hole emits excess energy and settles into a stable state. The most important part concerning today’s paper is the merger and the ringdown.
The Merger
During the merger, the two black holes significantly distort the spacetime resulting in a remnant black hole that has a very complicated geometry. Computationally intensive simulations that solve Einstein’s equations on supercomputers are required to fully describe the distorted remnant during the merger phase.
Sometime after the merger, the remnant will stabilize by releasing energy through gravitational waves. Eventually, the geometry of the stable black hole can be simply described using what is called the Kerr geometry We call this the ‘ringdown’ because the process is very similar to how a bell rings down after being struck.
The Ringdown
How do we describe the ringdown? While a black hole is in the ringdown phase, it is in a perturbed state, just like a bell that has been rung. The bell, like any other musical instrument, rings down through a sum of many different modes which are just damped sinusoids. Each mode has a unique frequency and amplitude, but the amplitude decays with time as energy is released by the bell. A perturbed black hole is very similar. The way we can describe both the bell and the black hole in the same mathematical framework is through a tool called perturbation theory. We can approximately describe the spacetime during the ringdown as the Kerr spacetime with small corrections. If the perturbation has a small size of ε, the first correction to the (Kerr) spacetime of the perturbed black hole is small by a factor of ε, and the second correction a factor of ε^2, and so on. The machinery of perturbation theory allows us to arbitrarily improve our solution to the perturbed black hole by finding higher and higher corrections.
The Paper in a Nutshell
Now what does all this have to do with the paper you ask? Thus far, almost all models describing the ringdown modes of the black hole have focused on using ‘linear perturbation theory’, where they stop with corrections of order ε. According to linear perturbation theory, the ringdown modes of a black hole have a fundamental piece as well as overtone contributions, which are like the higher frequency notes of your musical instrument.
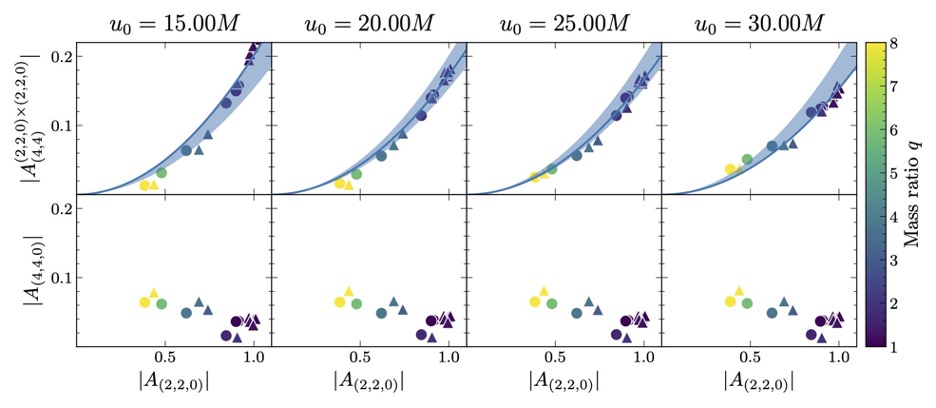
However, linear perturbation theory is only an approximation and higher-order corrections have to be included to improve the accuracy of describing the ringdown. Recently, perturbation theory has been extended to include (higher-order) quadratic i.e., ε^2 corrections (refs [31-41] in the paper). The main takeaway about the quadratic contribution is that they are nonlinear, as they are generated by the linear contribution to the ringdown. In other words, the ringing causes more ringing – a prediction coming from the nonlinear nature of Einstein’s general relativity, which is our current best understanding of gravity. A feature of the nonlinear modes is that the amplitude of the quadratic quasinormal mode is essentially the square of the amplitude of the linear quasinormal modes. The authors indeed find this quadratic behavior by fitting the amplitudes of the ringdown from the nonlinear model to numerical relativity simulations (see Fig. 1). The punchline is that the nonlinear modes are indeed present in the data from the simulations.
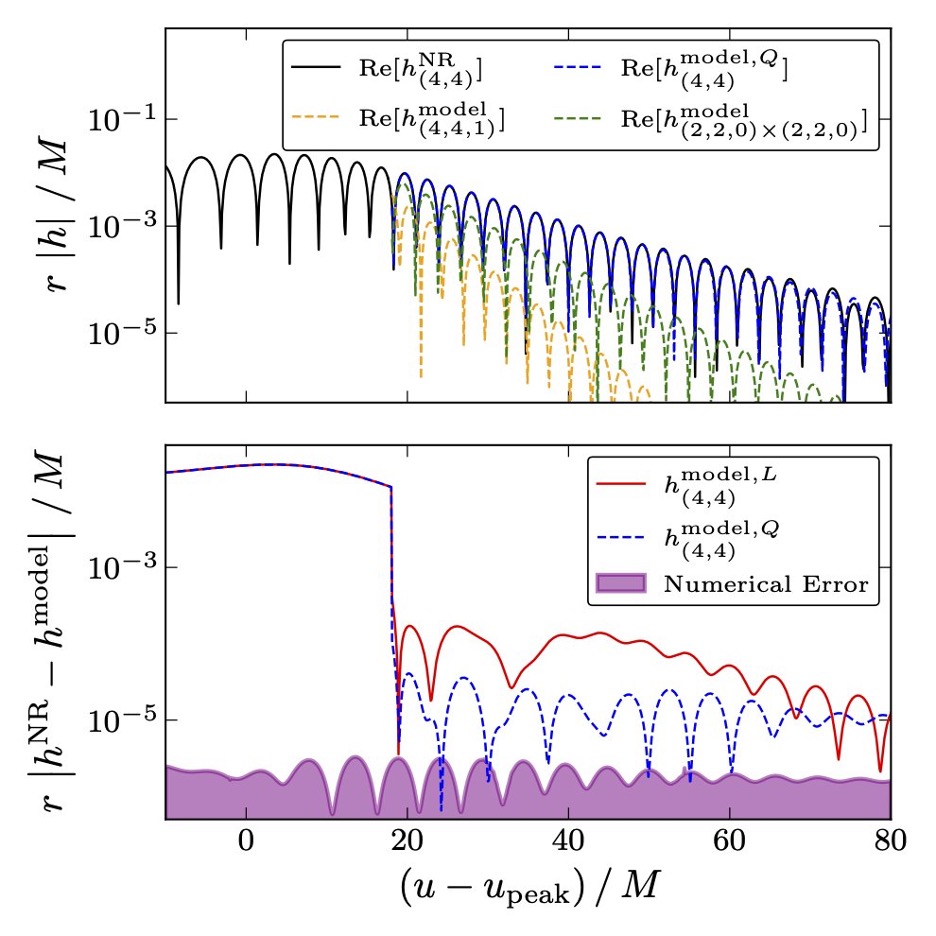
The authors in this paper question the validity of using linear perturbation theory to describe the ringdown part of the gravitational wave. Specifically, the authors show that by including quadratic quasinormal modes, the models describing the ringdown improve significantly! We can see this improvement in Fig. 2, where the model with the quadratic contribution fits the numerical relativity simulation of a black hole ringdown better than the model with only linear quasinormal modes. They also show (seen in Fig. 2) that the quadratic contribution can be more significant than the higher overtones of the linear quasinormal modes.
For upcoming gravitational wave observations, the authors’ work shows the importance of including nonlinear effects from perturbation theory. The authors’ work has shown that (1) including nonlinear modes more accurately describes the ringdown and (2) the nonlinear modes can be more dominant than higher overtones of the linear modes of the ringdown. For any perturbation theory to be valid, one would expect that nonlinear effects are subdominant. However, given that the authors’ results show that nonlinear modes can be more dominant than higher overtones of the linear modes, there are open questions of whether we can even use the machinery of any perturbation theory.
The important takeaway from this paper is that we (as a community) have just scratched the surface of investigating nonlinear effects of the black hole ringdown and that several more studies will follow that will provide more insight into such nonlinear effects. Improving the accuracy of black hole ringdown models is critical to our understanding of gravity in the strong field regime. Accurate models impact our ability to measure parameters from the gravitational wave data of merging black holes. Precision measurements of the properties of the remnant black hole, from the gravitational wave, allow for several strong field tests of general relativity and such tests are critical to determining potential deviations from Einstein’s theory. Future gravitational wave detectors can be precise enough to necessitate more accurate models and this paper has shown that our models need to be improved!
Edited by: Jenny Calahan
Featured Image Credit: Cartoon by C.V. Vishveshwara.