Paper: Probing lens-induced gravitational-wave birefringence as a test of general relativity
Authors: Srashti Goyal, Aditya Vijaykumar, Jose Maria Ezquiaga, Miguel Zumalacarregui
Author Institutions: International Centre for Theoretical Science, Tata Institute of Fundamental Research; Department of Physics, The University of Chicago; Niels Bohr International Academy, Niels Bohr Institute; Max Planck Institute for Gravitational Physics
Status: Submitted to arXiv [12 Jan 2023]
General relativity (GR) is undoubtedly an extremely successful theory of gravity, having passed all experimental and observational tests so far. Nonetheless, alternative theories of gravity are actively explored for various theoretical motivations, such as explaining the accelerating expansion of the universe. One such example is a scalar-tensor theory which includes a scalar field in addition to the tensor field (the ‘metric’ tensor) which GR is based on. However, such a theory is of little use if it cannot be tested. Fortunately, the authors of today’s paper propose a method for testing GR and its possible extensions by studying the ‘scrambling’ of gravitational waves (GWs).
GW Modes
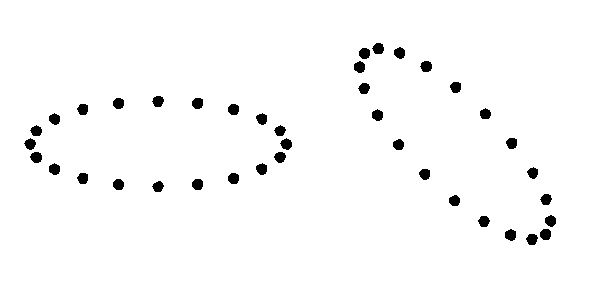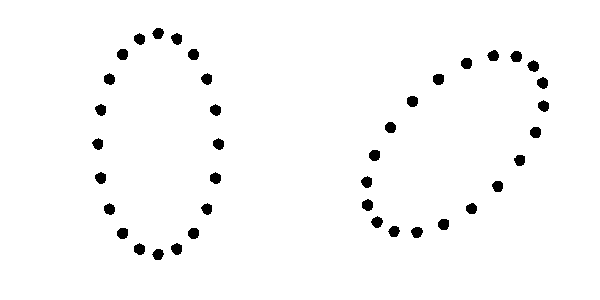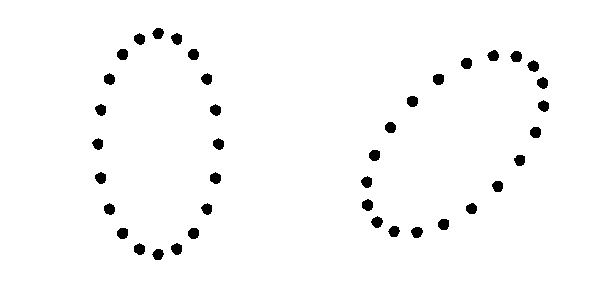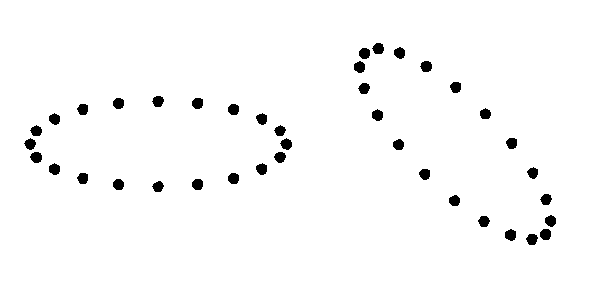
GWs, like electromagnetic waves (light), have a property called polarization which describes the geometry of the wave oscillations. GR predicts the existence of only two polarization modes for GWs: the tensor plus (+) and cross (×) modes (Figure 1). In GR, the two modes propagate independently from each other and move at the speed of light. The evolution of a GW is described by a sum of the independent evolution of the two (+ and ×) modes.
The situation differs in alternative theories of gravity with extra degrees of freedom (such as an additional scalar) which allow additional GW polarizations. The extra modes can appear and mix as the GWs propagate. In particular, in scalar-tensor theories, regions of strongly curved space can lead to interactions between the tensor and scalar degrees of freedom that cause the standard + and × modes to move at different speeds. Thus, studies of only the propagation of the modes allowed by GR can also probe signatures of additional modes forbidden by GR. The existence of additional modes would indicate a violation of GR and require an extension of the current model of gravity! But how does one go about searching for such a signal?
How to Scramble GWs: Lens-Induced Birefringence

The authors study the difference in the propagation speeds of the + and × modes in an effect called lens-induced birefringence (LIB). An analogous effect which may be more familiar (and illustrative) is optical birefringence in crystals. Under this effect, light incident on an anisotropic crystal undergoes double refraction and is split by polarization into two rays that travel with slightly different velocities. This produces two images, one slightly displaced from the other (Figure 2).
In the case of GWs, birefringence occurs when a large mass, such as a super massive black hole or galaxy, splits the original signal by polarization mode and speed (which may differ among the modes in non-GR theories) depending on the incident position and direction (Figure 3). This separation causes each polarization mode to arrive at the GW detector at a different time, resulting in a relative time delay between modes– the main observable in this study.
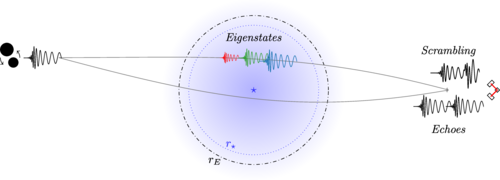
Effects of Scrambling
If the delay between the two tensor modes is shorter than the total duration of the signal, the waveform is distorted or “scrambled” due to the interference of the polarizations. In this paper, the authors look at the difference in the arrival times between the two GR polarization states due to different propagation speeds as a result of LIB.
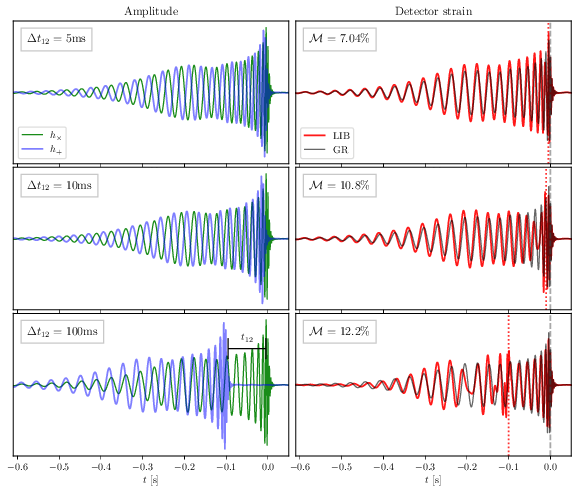
They calculate the GW signal measured at the detector after LIB ‘scrambling’ (of the polarization amplitudes) by a spherically symmetric lens as a function of the time delay and angle between the lens and source (relative to the direction of GW propagation). Under LIB, the polarizations interfere, leading to waveform distortions. The authors quantify the distortions due to GW birefringence by computing how much the birefringence ‘scrambles’ the GR signal. Examples are shown in Figure 4.
Taste Test (i.e. Results)
The authors apply their time-delay analyses to GW signals from merging binary black holes and neutron stars detected by LIGO-VIRGO. They find that almost all events were consistent with no LIB time-delay, i.e. GR. Only a few events show a preference for LIB. Upon further analysis, they conclude that there is no strong evidence for birefringence in the data.
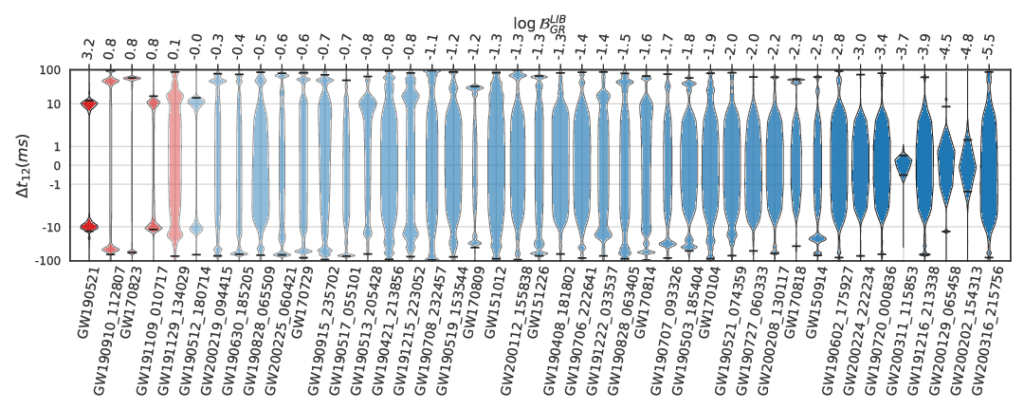
This non-observation of birefringence in the events analyzed translates to constraints on the phenomenological model parameters. As an example, they apply their results to a specific scalar-tensor theory of gravity which predicts LIB and places constraints on parameters in that theory.
Although the authors find no strong evidence for birefringence, they note that with improving detector sensitivity, measurements of smaller birefringence time delays which may be missed in current data will be possible. This will allow better constraints on birefringence probabilities.
Furthermore, developing LIB predictions for other alternative theories of gravity and applying the results of this work will offer more tests of the landscape of theories beyond GR.
Astrobite edited by Katya Gozman
Featured image credit: modification of Fig. 4 of the paper