Title: Detecting High-Frequency Gravitational Waves in Planetary Magnetosphere
Authors: Tao Liu, Jing Ren, Chen Zhang
Author Institutions: Department of Physics and Jockey Club Institute for Advanced Study, The Hong Kong University of Science and Technology and Institute of High Energy Physics, Chinese Academy of Sciences
Status: Submitted to arXiv
Gravitational waves (GWs) with frequencies beyond the reach of current detectors are referred to as ‘high-frequency.’ For reference, LIGO and Virgo reach the highest frequencies up to about 10 kilohertz. Gravitational waves at higher frequencies could have been produced by exotic astrophysical objects (such as primordial black holes and boson stars) and cosmological events in the very early universe (e.g. phase transitions and inflation). These signals are particularly challenging to detect because they are expected to be very weak. Today’s authors propose a method and a new (but already existing) laboratory for detecting these waves.
The Inverse Gertsenshtein Effect
Direct detection of GWs is challenging because the waves are very weak and only disturb spacetime by a small– barely measurable– amount. Interferometers, for example, directly measure the vibrations from only some of the most extreme events (such black hole and neutron star mergers). GWs can also be detected indirectly by measuring their effects on other systems or by detecting phenomena that result from GWs. One such effect is the inverse Gertsenshtein effect.
) and photons/EM waves (
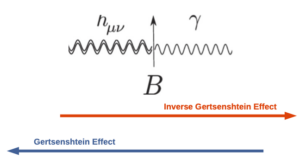
) in a magnetic field (B). (Modification of Figure 1 of Domcke & Garcia-Cely 2021)The Gertsenshtein effect was first proposed in 1961 by– you guessed it– a physicist named Gertsenshtein. This effect describes the conversion of photons (carriers of the electromagnetic force) to gravitons (hypothetical particles that carry the force of gravity) in the presence of a magnetic field. The opposite of this process, aptly named the inverse Gertsenshtein effect (see Figure 1), describes the conversion of gravitons to photons, or GWs into electromagnetic (EM) waves (aka light).
We already know how to detect a wide range of electromagnetic frequencies; EM waves are very well studied and there is a multitude of experiments exploring all scales of the universe. Sensitivity to EM waves at high frequencies translates to sensitivity to high-frequency GWs per the inverse Gertsenshtein effect. For decades after this effect was proposed, it was believed that the strength of the interaction between gravitons and photons was too small for the effect to ever be of experimental interest. Making the effect measurable would require a very (astronomically!) large magnetic field. Fortunately, those exist. Enter: planetary magnetospheres.
Magnetospheres
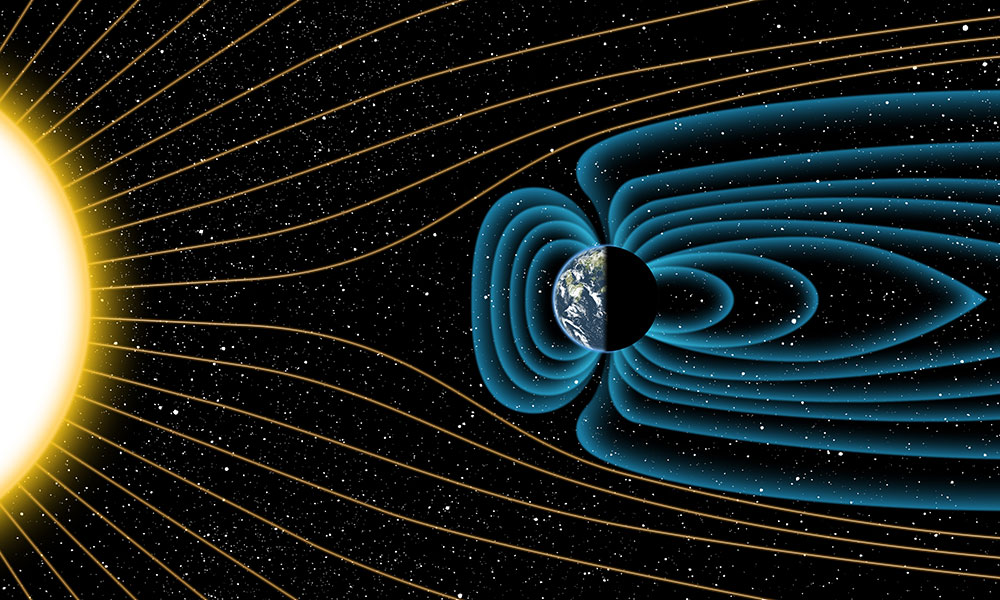
A magnetosphere is a region of space around an astronomical object (like a planet) dominated by the object’s magnetic field. Earth’s magnetic field, generated by the motion of charged, molten iron in the planet’s core, forms a magnetosphere that stretches far into space and shields the planet from harmful solar and cosmic radiation (see Figure 2).
Earth has the strongest magnetosphere of all the rocky inner planets (n.b. Venus and Mars don’t have any), while the award for the largest and most powerful planetary magnetosphere in the solar system (and– fun fact– also the largest structure in the solar system other than the heliosphere) goes to Jupiter. Both Earth’s and Jupiter’s magnetic fields are large enough to make the probability of the inverse Gertsenshtein effect occurring practical for detection. This makes them compelling laboratories for high-frequency GW detection.
Conversion probability
The experiment requires measuring the photons produced by GWs via the inverse Gertsenshtein effect in a planetary magnetosphere. The probability that a graviton/GW traveling through a magnetic field will be converted into a photon/EM wave is called the conversion probability.
The authors consider a satellite-based detector positioned at a certain latitude and altitude above a planet’s surface. They then compute the conversion probability of high-frequency GWs hitting this detector in all directions. The probability depends strongly on where the detector is located and the direction it is pointing. This is because the length of the path over which the conversion can happen depends on both of these factors. A careful design for the orbit of the satellite to maximize the conversion probability is important for efficient and optimized detection.
Detection prospects
There are already instruments around both Earth and Jupiter that allow estimates of upper limits on the GW-photon conversion in their magnetospheres. This can be used to estimate limits on stochastic GW detection. In the analysis, the authors consider a stochastic background of gravitational waves that are isotropic (the same in every direction) and stationary.
In Earth’s magnetosphere, the authors use the Suzaku satellite, an X-ray astronomy satellite operating in low earth orbit. Recall that X-ray photons have frequencies of order order 
Challenges
A challenging part of measuring this effect is the background noise. The fluxes of both the signal and background photons have angular and time dependence for a detector at any given orbit. To measure the photons converted from GWs, one has to subtract out the background photons– the contribution that doesn’t come from the inverse Gertsenshtein effect. Around Earth, there are many complex processes to model and account for over a wide range of frequencies, such as the cosmic background (with frequency-dependent reflectance in the atmosphere), atmospheric thermal emission in the infrared band, and Ozone absorption of background light.
New detection method?
Today’s paper proposes a novel method for detecting high-frequency (stochastic) GWs traveling through planetary magnetospheres. This method has the potential to cover the full frequency band of electromagnetic signals in observational astronomy, which includes the possibility of detecting gravitational waves at high frequencies. The authors provide a proof-of-concept for this method and propose next steps that include: exploring ways to orientate the detector for higher conversion probability and reduced background, and performing dedicated studies to Jupiter and even the Sun, which both have stronger magnetic fields and larger effective GW-photon conversion regions than Earth.
Astrobite edited by Junellie Gonzalez Quiles
Featured image credit: NASA (modified by author)
