This guest post was written by Mingchen (Michelle) Wang, an undergraduate studying Statistics and Data Science at UCLA. She is passionate to explore fields where statistical analysis and astronomy combine. Mingchen wrote this article as part of a science journalism class taught by Astrobites author, Briley Lewis.
Title: A Measurement of the Kuiper Belt’s Mean Plane From Objects Classified By Machine Learning
Authors: Ian Matheson, Renu Malhotra
First Author’s Institution: Department of Aerospace & Mechanical Engineering, University of Arizona, Tucson, AZ 85721, USA
Status: Posted to arXiv
How large is our galaxy donut?
A collection of small icy bodies form a donut-like shape that orbits around the sun. This donut, known as the Kuiper Belt, lies further than the orbit of Neptune in our solar system. Like the Asteroid Belt, but far larger, it is a region of leftovers from the solar system’s early history. It is home to millions of Kuiper Belt objects (KBOs), trans-Neptunian objects (TNOs), and also to many dwarf planets, including Pluto, Orcus, Haumea, and Makemake.
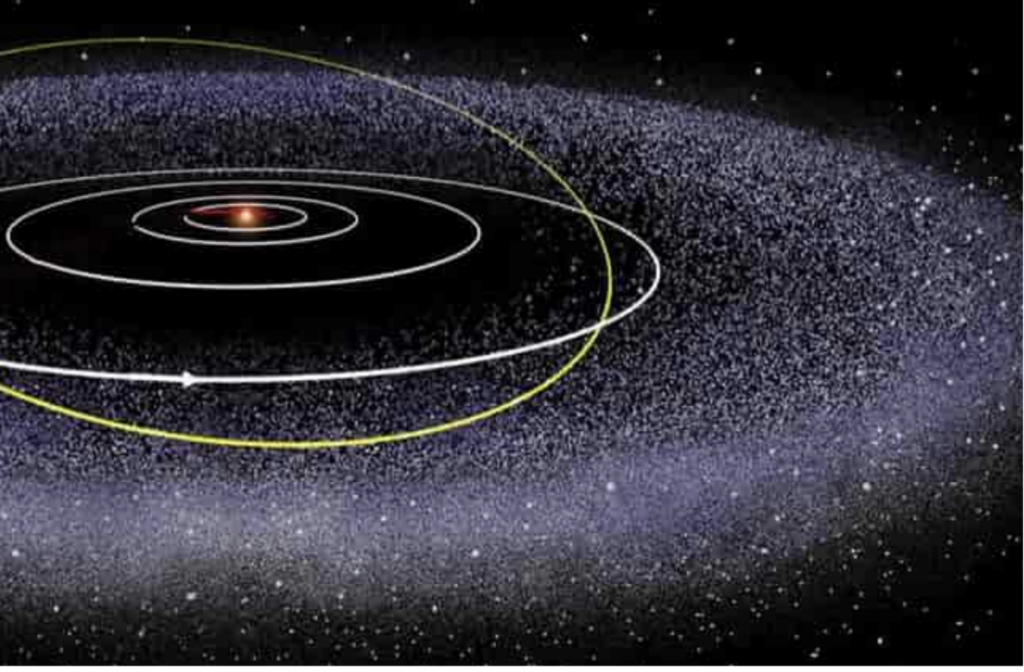
For decades, scientists have extensively studied the Kuiper Belt. Previous measurements concluded that this belt stretches from roughly 30 to 55 AU, but that is a lot of uncertainty! For reference, one astronomical unit (AU) is about 93 million miles. An uncertainty of 1860 million miles doesn’t seem too good, right? Well, you are in luck! This paper walks through a concept of finding an accurate measurement for the size of the Kuiper Belt, specifically using machine learning techniques. After all, machine learning is great at handling large amounts of data and simulations, just like ChatGPT.
Oh no, Researchers are starting a fight…
When we have millions of particles in the Kuiper Belt plane, how do we determine where each one of them may be? This is when a bit of data modeling comes into play. Previous researchers focused on a theory that introduced the idea of a Laplace surface, a two-dimensional surface that represents the density of KBOs in three-dimensional space. Others decided to calculate an invisible plane (called the solar system’s invariable plane) that passes through the solar system’s center-of-mass as a candidate for the ecliptic plane (an imaginary plane of Earth’s orbit around the Sun) of the Kuiper Belt. However, these measurements yielded inconsistent results as they predicted different inclinations and longitudes of the plane. Some researchers rejected the Laplace surface, some rejected the invariable plane below certain values of the semimajor axes of the Kuiper Belt, while others concluded that they could not reject either.
Well, let’s join this fight!
Instead of changing the data to fit a model, the authors generated a statistical distribution where the KBOs are modeled to have lower eccentricities than the average, and similar tilts to average KBOs. Then, they use a machine learning-based program that predicts possible outcomes of an uncertain event (known as a Monte Carlo Simulation) to account for bias in calculation. For each of the KBOs in the simulation, these objects are then assigned orbits randomly based on a statistical model of KBOs in real life. The program compares the properties of each simulated project to those of real objects, to ensure that the sample represents the biases. They repeat this experiment and calculate the size of the model each time with a new randomly assigned orbit for each object. This mass random generated list by computers form a predictable pattern, where machines can estimate the most possible positions and orbits of the KBOs, and use this to calculate how likely it is for the plane to be a certain size.
A successful machine learning experiment needs a large dataset. The bigger the dataset is, the more data a computer can use to recognize patterns. Luckily for us, we have the data from JPL Solar System Dynamics Group’s Small Body Database Query, which contains almost all asteroid-type objects. With some cross-referencing on different databases, the authors were able to create a dataset that is large enough for us to continue our simulations.
Tell us what you got, ChatGPT
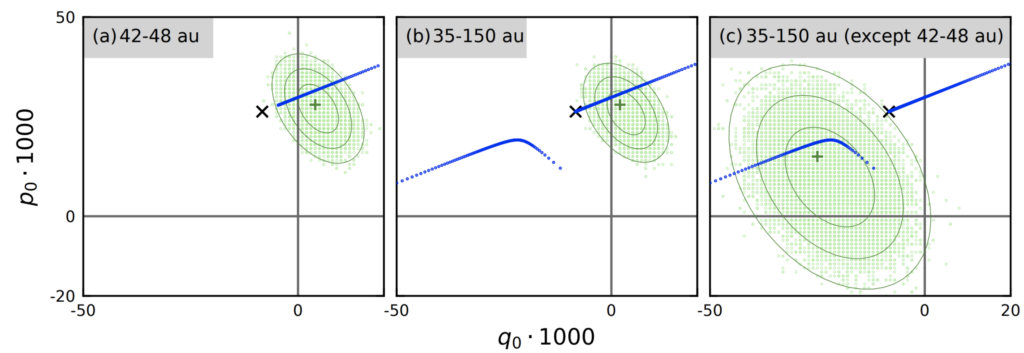
The authors were able to develop a calculation for the size of Kuiper Belt and its uncertainty, based on the machine learning technique discussed in the previous paragraph. Figure 2 is a model of the Kuiper Belt in an area represented by (p,q), parameterised representations of the inclination angle.
In the figure, (a) is the classic measurements, (b) is the entire belt from 35-150 AU, and (c), the entire belt minus part (a). The best-fit plane developed from a series of datasets is shown in dark green “+”, while the confidence levels are represented by the green circles around. The simulations of the 40000 Monte-Carlo samples are in light green. The invariable plane, proposed by other scientists is represented by the black “x”, and the theoretical prediction for the Laplace surface is plotted in blue. Since “x” is well outside the contours, the researchers have concluded that the invariable plane can be rejected because it is too far away from their calculations, but the Laplace surface cannot be rejected as it still lands in the uncertainty intervals based on the simulations.
All in all, this research is able to establish a more accurate measurement for the size of the Kuiper belt. This is a great step in the field of astronomy, and it allows future researchers to develop theories on exoplanets and extraterrestrial life. There is still much more in space waiting for us to discover, and more accurate measurements of our Kuiper Belt is only the beginning.
Astrobite edited by William Lamb