Title: Resonant Scattering of Gravitational Waves With Electromagnetic Waves
Authors: Ruodi Yan and Yun Kau Lau
First Author’s Institution: Department of Physics, Beijing Normal University
Status: Published In Chinese Physics Letters [closed access]
Gravitational laser beams may sound futuristic or even impossible, but that doesn’t stop physicists from exploring their possibility. The authors of today’s paper propose that a description of spacetime (a mathematical model of the three spatial dimensions + time) that includes the interaction between gravitational waves (GWs– see our guide to them here) and electromagnetic (EM) fields could generate an intense beam of GWs, somewhat similar to a laser. Why might this “gravilaser” be useful, and how does it actually compare to a laser? Read on to find out!
What is a laser anyway?
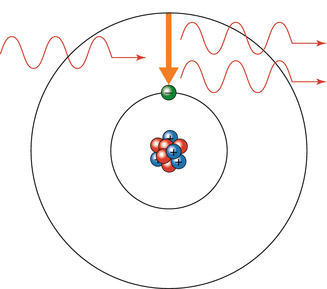
To understand how one might produce a “gravilaser,” it is helpful to understand how its electromagnetic (EM) analogy, a free-electron laser (FEL), operates. First, we should note that a FEL is different from a conventional laser (which stands for Light Amplification by Stimulated Emission of Radiation). A conventional laser hits excited atoms or molecules with photons, which stimulate the emission of more photons of the same frequency by causing electrons in the atoms or molecules to drop energy levels, thus amplifying the number of photons (Figure 1).
One shortcoming of the conventional laser is that its tunability is limited: the frequency of the light depends on the energy levels of the atoms or molecules used. A FEL is an alternative which overcomes this tunability limitation. In this “laser,” electrons are pumped into a changing magnetic field created by an arrangement of magnets– the technical term is “undulator” or “wiggler,” describing what happens to the electrons that move through it. This field causes the electrons to release some energy as photons, which are eventually emitted as a coherent beam of light.
In this laser design the electrons are free– not bound to an atom or molecule, as they are in the case of conventional lasers– so the light can be tuned to any frequency by adjusting the energy of the initial electrons and the parameters of the undulator. There is also a resonance condition which must be met: the frequency of the photons must be tuned to the oscillations of the electrons in the undulator in order to produce a coherent beam of light (Figure 2).
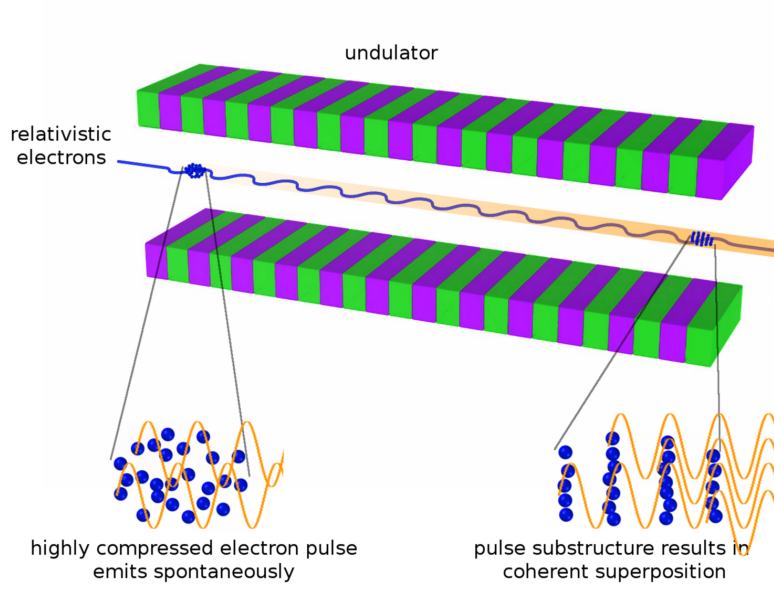
The authors compare their hypothetical gravilaser to the FEL: the underlying operational principles are different, but both produce intense beams of radiation– one gravitational (gravitational waves) and the other electromagnetic (light) – and each depends on a resonance condition between the emitted radiation and the radiation that produces it.
Gravilaser
, and the lower shows a component of the electromagnetic field, 
, as a function of time coordinate u. Note that the changes in the two fields are correlated: increases exponentially at the expense of .So how does one generate a “gravilaser”? To start off, we need a gravitational theory– foundational for studying gravitational radiation! The authors choose to work within the context of Einstein’s general relativity, a standard and well-agreed upon choice. Next, we must describe the spacetime (this is what the gravitational waves, and everything else, exist and propagate in). The authors consider an Einstein-Maxwell description of spacetime, that is, a model that describes both gravity (per Einstein’s theory of general relativity) and electromagnetism (described by Maxwell’s equations). What is essential about this choice is that it allows us to describe the way classical electric and magnetic fields affect the geometry of spacetime, and vice versa.
One class of possible solutions to the equations describing this spacetime allows for scattering of GWs and EM waves. These solutions have an instability, which means that the result is highly dependent on initial conditions: a small change can lead to a very different outcome. The authors then try to work out the implications of this on the electromagnetic and gravitational fields.
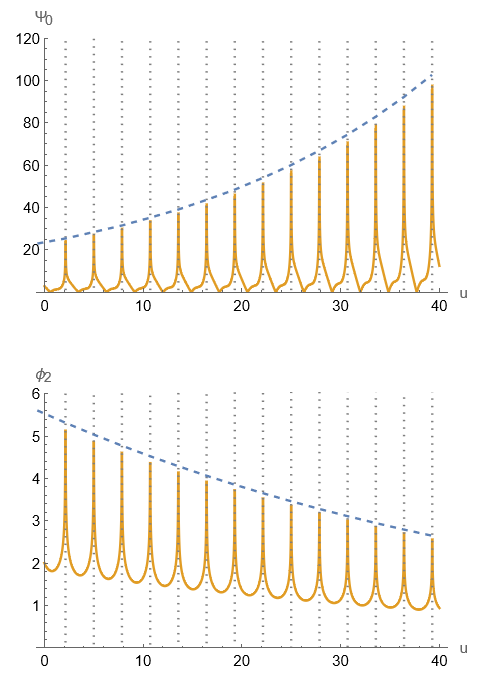
What they find is that when a certain resonance condition– more complicated than the resonance condition in the FEL– is met, electromagnetic energy is transferred to the gravitational field (Figure 3). This energy transfer is coherent in the sense that the increase in a component of the gravitational field and decrease in a component of the EM field happen at the same frequency. And, similar to the FEL, the frequency of the gravitational component is tunable by adjusting components of the EM field.
Prospects & Applications
This work points out that an intense “beam” of GWs can be generated by the conversion of EM energy into gravitational energy if a certain resonance condition is met. This is in some ways similar to coherent emission of photons by a FEL, which also relies on a resonance condition. The authors indicate two reasons why this is interesting. First, it offers hope (even if very remote) that a gravilaser could be generated in a laboratory. Currently we rely on sources from space for detectable GW signals. Second, this idea may help in the detection of GWs from an astrophysical source. In the case that we already know the frequency of the wave we are trying to detect, EM energy could be pumped in to enhance the amplitude of the GW signal, thus enhancing the ratio of the signal over the noise, improving and or allowing for the detection of very faint signals.
Astrobite edited by Lucas Brown
Featured image credit: modified Figure 2 of the paper
