Title: Relativistic drag forces on black holes from scalar dark matter clouds of all sizes
Authors: Dina Traykova, Rodrigo Vicente, Katy Clough, Thomas Helfer, Emanuele Berti, Pedro G. Ferreira , and Lam Hui
First Author’s Institution: Max Planck Institute for Gravitational Physics (Albert Einstein Institute),
Am Mühlenberg 1, Potsdam-Golm, 14476, Germany
Status: Submitted to Physical Review D [Open Access]
This bite was written and published as part of Astrobites’s new partnership with the American Physical Society (APS). As part of this partnership, we cover selected articles from the Physical Review Journals, APS’s premier publications covering all aspects of physics. For more coverage as part of this partnership, see our other PRJ posts.

In the 91 years since the term “dark matter” was coined and the 60 years since its existence was essentially confirmed by Vera Rubin, astrophysicists have been scratching their collective heads about what dark matter actually is. Our current best model of cosmology, Lambda-Cold Dark Matter (LCDM), does a pretty good job of explaining the behavior of dark matter on large scales, but seems to break down a bit when applied to small scales (reality check: by “small-scales” we mean the size of galaxies). As experiment after experiment slowly chips away at the possibilities of the nature of dark matter, astrophysicists have come up with increasingly creative ways to measure the properties of dark matter. Today’s paper represents a particularly bodacious example, the authors ask: when black holes merge, do they wakeboard on dark matter waves?
Dark Matter Waves? Particles? Both?
If you’ve been hanging in physics or popular science circles for long enough, you’ve probably heard of the wave-particle duality: the fundamental building blocks of the universe sometimes behave like little billiard balls (particles) and other times like waves in the ocean. We know this thanks to a myriad of experiments, most famously the double-slit experiment. To put a bit of a finer point on this idea, every particle has a wavelength, called the deBroglie wavelength, that depends upon its mass: lighter particle = longer wavelength. The length of this wavelength gives a rough estimate of where the particle tends to go from behaving more like a particle to more like a wave. If the particle is very light, that wavelength could be very long, and therefore the particle could behave like a wave even on astrophysical size scales.

This raises the possibility that massive objects like black holes could interact with these particles as though they behaved like normal, ocean-style waves. This means that black holes can develop a “wake” of dark matter that forms behind them as they move through the black hole similar to an object moving through a fluid, see Figure 2. This dark matter wake is formed through a process called dynamical friction and could lead to a noticeable effect on the gravitational waves emitted by merging black hole binaries. Essentially, if black holes are forming dark matter wakes as they inspiral during a merger, the release of gravitational waves will be more sluggish thanks to the drag created.
Today’s authors want to determine how to best model this effect to see how it could be measured by future gravitational wave observatories. They also want to model the effect of “momentum accretion”. A black hole sucks up dark matter as it moves through it and therefore gains the momentum of the dark matter it absorbed thanks to good ol’ conservation of momentum, but that didn’t make as snappy of a title for the astrobite, so we’re sticking to the wakeboarding theme. Generally, the momentum accretion plays a smaller role than the dynamical friction, but the authors point out that these roles may reverse in certain scenarios. In order to study these effects, the authors want to build their dark matter theory from the ground up in order to make calculations analytically (think pencil and paper style math, actually writing down equations) and simulate it numerically.
I, the author, have tricked you into learning about Quantum Field Theory
The authors of today’s paper start by laying out the framework for how they want their theoretical dark matter to behave. They do this by defining an action, a quantity that describes how an object’s energies change as it moves along a path. For our purposes though, we can think of the action as the set of rules we want our particle to obey. The action specifically describes how the dark matter particle field behaves. A particle field is a theoretical quantity that permeates all of space, and Quantum Field Theory supposes that every particle is made from a little clump of this field: electrons are clumps in an electron field, quarks are clumps in a quark field, you get the picture. After a few frantic WhatsApp messages to my field theorist colleagues for reassurance that I actually know what I am talking about, we can basically understand the weird looking symbols in the action like this:
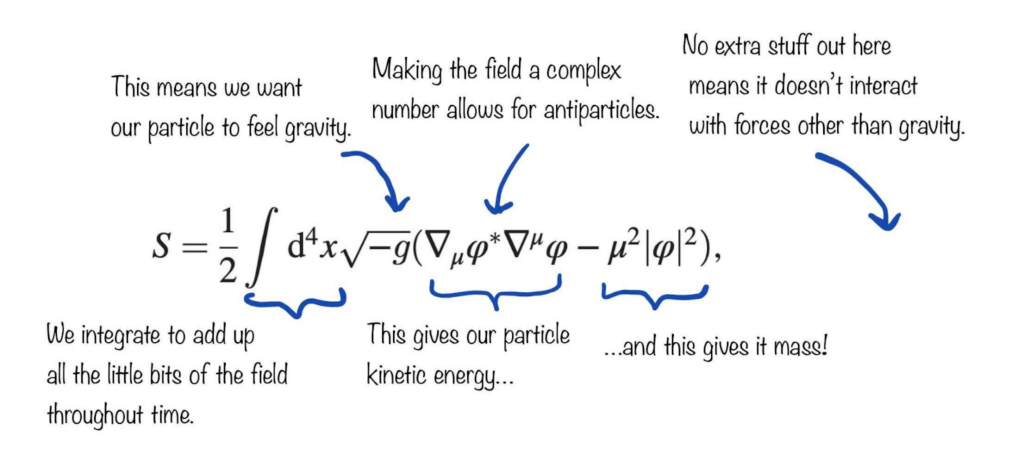
Now that we have the rules for how our dark matter field behaves, we need a place to test it! This is where General Relativity (GR) comes in. GR has a quantity called the metric, which is a mathematical object that describes the stage that physics takes place on. For example, you and I are currently sitting in a region of spacetime that is relatively flat, but around a black hole spacetime is very curved, so the metric is quite different. Thankfully, the stage setting for a black hole is already well known, the Schwarzchild metric, which you have probably seen versions of before in all manner of sci fi-esque illustrations. Now that we have our rules for how the field behaves (the action) and the background that we are testing it on (the metric) the authors can plug and chug to find expressions for the dynamical friction and the momentum accretion of the black hole.
How well do blackholes wakeboard?
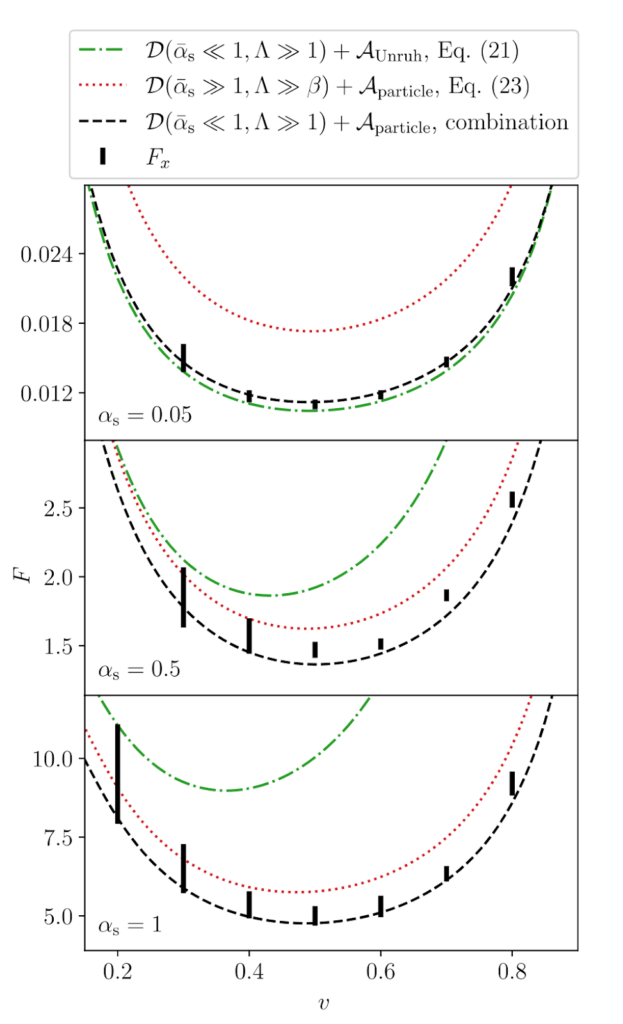
When doing hard physics problems, it is often easier to think about special cases rather than trying to solve the whole problem at once. That is exactly what our authors do here; they tackle this problem by looking at specific cases, such as where the particle is very light, or the cloud of dark matter is very large. The authors note that there are certain scenarios where writing down analytic equations is impossible, and hence they turn to numerical simulations. Their results, which compare their analytical results to their numerical results, are shown in Figure 4.
Their results show that analytic expressions for the forces affecting the black hole are relatively good, but vary in effectiveness depending on the dark matter particle mass. Remember when we talked before about the deBroglie wavelength, and how it set the scale for where a particle behaves more like a wave versus more like a particle? When the particle is very light, using equations for dynamical friction and accretion where the particle behaves like a wave (green line) seems to work quite well, but of course begins to break when we get to higher mass meaning the dark matter behaves more like particles. Doing the opposite, using equations that describe dynamical friction and accretion as though dark matter was a particle (red line) seems to work well for heavier particles but breaks for lighter particles. Interestingly, a franken-combination of the two, using an equation for dynamical friction that treats dark matter like a wave while the accretion equation treats it like a particle, seems to match the simulations in all three of the cases.
Future Directions
Understanding how black holes interact with dark matter could be key in determining what dark matter actually is. The authors note that LISA, a future space-based gravitational wave observatory, could likely notice the drag effects of the dynamical friction and momentum accretion on the gravitational waves released by merging black holes. If we could measure the effects of these forces, we can infer the properties of dark matter, such as its mass. However, in order to do this, we need a realistic model of how the black holes will interact with the dark matter, and today’s authors have started us down the road to doing just that. While the agreement between analytic expressions and simulations is extremely promising, the authors point out that they’d like to make their models even more sophisticated. For example, the black holes would likely be spinning, the dark matter field may interact with itself, the effect of the dark matter field on the space time background could be significant, (the authors plop the field on the spacetime in this paper, without worrying about if the field itself could bend the spacetime, which is a good assumption for a light particle), or the dark matter particles could have spin. Even with all these potential extensions, the results of this paper are quite an exciting prospect for determining the properties of dark matter through new methods. As our understanding of the interplay between dark matter and the surrounding universe gets better and better, the true nature of dark matter has less and less places to hide, and we will hopefully have a better understanding of one of the most mysterious concepts in astrophysics in no time!
Astrobite edited by Janette Suherli
Featured image credit: Wikimedia Commons + Edits by Kat Nurminsky.