Title: Probing new physics on the horizon of black holes with gravitational waves
Authors: Elisa Maggio
First Author’s Institution: Max Planck Institute for Gravitational Physics
Status: Submitted to Arxiv [Open Access]
The universe is surprisingly shy when it comes to singularities. A gravitational singularity is a point experiencing such extreme gravity that it breaks the structure of spacetime, at least as we understand it. At the singularity, our current best model of gravity- General Relativity– predicts infinite gravity or something else completely nonsensical. The classic example of a singularity is the center of a black hole, where theoretically matter is compressed to an infinite density with infinite gravity. Physicists are extremely curious about what is actually happening at these singularities, but the universe, shy as it is, hides all of its singularities behind event horizons. The event horizon is the point of no return for anything around a black hole, not even objects moving at the speed of light. Since light cannot escape past the event horizon, we are completely unable to observe any of these singularities. This leads to a sort of uneasy truce between physicists; sure maybe our theory of gravity is definitely wrong at certain spots, but all those spots have been effectively swept under the rug, so maybe it’s all fine for now? However, if we want a completely correct theory of gravity, it needs to be true everywhere. Some modern alternate gravity theories have a bold solution to this issue: what if there was no horizon and no singularity? Could we have objects that behave like black holes but have no event horizon? Today’s Astrobite explores a paper that seeks to hunt for these horizonless compact objects using the gravitational wave signal emitted when they collide!
Black Hole Wiggles

Gravitational waves, observed for the first time recently in 2017, have already become an amazingly useful tool for studying some of the most extreme events in our universe, such as black hole mergers. When two black holes collide, they go through 3 phases: an inspiral phase, where they spin around each other as they get closer and closer, a merger phase, where they combine into one black hole, and a ringdown phase where the new black hole wiggles around a bit as it settles down into a new stable black hole. The author of this paper argues that this ringdown phase is the key to determining whether the new black hole has a horizon or not. (Since a black hole isn’t really a black hole if it doesn’t have an event horizon, I’ll start calling these theoretical objects horizonless compact objects or HCOs for short.)
So how can we tell if our resulting object is a black hole or HCO? Well, let’s talk about those wiggles. Systems that oscillate (fancy word for wiggle) tend to have what is called normal modes. A normal mode is when all parts of your system oscillate at the same frequency and don’t fall out of sync. Normal modes are extra special because if you know them, you can use them to describe any oscillation the system does! This is extremely useful for physicists, who would love to do as little math as possible, thank you very much. The problem is, we know our black hole won’t go on wiggling forever, it will eventually settle down. Therefore, we actually need to find the quasi (latin for kinda) normal modes. Don’t let the invocation of a dead language scare you, this just means normal modes that eventually settle down over time.
Thankfully we have the tools to find these quasi-normal modes, using what is called the Schwarzhild metric. The Schwarzchild metric is a mathematical object that describes the curvature of spacetime around a non-spinning black hole. (Schwarzchild actually derived his metric while in the trenches of World War I, so when I am getting frustrated at my cosmology homework I try to find solace in the fact that I am not being shot at). The author takes the Scwarzchild metric and tests what happens when they nudge spacetime just a bit. In doing so, they can derive the frequencies of the quasi-normal modes and which ones are the most common. They can then repeat the process for a theoretical HCO. The HCO will differ from the black hole in two key ways. One, its lack of an event horizon means it is no longer immediately clear how big it should be, so the author defines a free parameter called the compactness of the object, related to its size. Secondly, while a black hole absorbs anything that crosses its event horizon, an HCO could have some reflectivity so the author also leaves that as a free parameter in their model. Repeating the calculation for the HCO, one finds that the quasi-normal modes will be different compared to the black hole’s! In general, they find that the HCO quasi-normal modes will be of lower frequency and take longer to settle down.
Where there’s wiggles, there’s (gravitational) waves
So we can tell the difference between a black hole and an HCO based on how it wiggles, but how will we measure how it is wiggling? Well, thankfully, when very massive objects move very quickly they can release gravitational waves which we can measure on Earth. The author then sets out to see what we would observe if the gravitational wave signal of an HCO in the ringdown phase were to be detected. To understand this different signal, we first need to discuss the photon ring, or light ring, of a black hole. The light ring earns this name as it is the radius at which photons can take circular orbits around a black hole. This ring (really a sphere all the way around the black hole) occurs at a distance that is particularly difficult to get past if you are trying to escape a black hole. It’s like the last hill on your bike home, really annoying to get over but once you’re past it you’re home free.
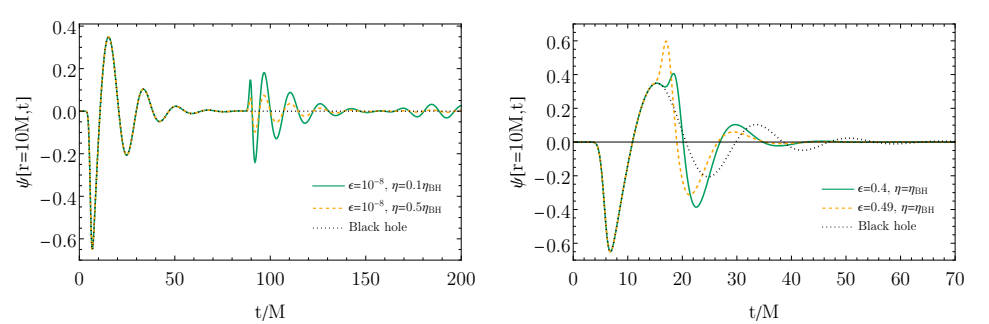
In the gravitational wave signal of a black hole, gravitational waves that cannot overcome this hill are reabsorbed when they are reflected back and contact the event horizon of the black hole. But an HCO has no horizon that would suck these waves back up, meaning that these gravitational waves can get trapped between the surface of the object and the light ring! They may bounce around in this trapped state for a bit before finally getting out at a later time, see Figure 3. This means an HCO might produce a gravitational wave “echo”, an initial burst of gravitational waves followed a bit later by the waves that were trapped.
Are these differences in signal detectable? Well, so far no detections of gravitational wave echoes have been made by any of the gravitational wave detectors that are currently online. However, planned next generation detectors like LISA or the Einstein Telescope will likely be powerful enough to either detect or rule out HCOs. With a confirmed detection of a horizonless compact object, we could learn a lot about the true nature of gravity and potentially uncover new physics!
Astrobite edited by Keighley Rockcliffe
Featured image credit: Wikimedia Commons

You made something really complicated, a lot of fun to read. Thanks for simplifying it!
Thank you so much! This was definitely one of the more theory-based Astrobites I have done. It was was really interesting to pore over!
While this is a great start, don’t you have to make it more real by using a spinning BH instead. Clearly most BH’s are spinning as that is practically impossible not to while spiraling in.
Hi Gary!
This is a great question and you are 100% right, it is nearly impossible for the resulting black hole to not be spinning. In this Astrobite we discussed the Schwarzchild metric which describes a static black hole; a rotating black hole like you’re mentioning is well described by the Kerr metric. The author of this paper does also use the Kerr metric to derive the properties of a horizonless compact object. However, gravitational waves will only be released by spinning objects if they are asymmetric; A perfect sphere spinning will not release gravitational waves, for example. (Mathematically, we say that the quadrupole moment of a system needs to be changing to release gravitational waves.) Since the Kerr black hole is symmetric about its axis of rotation, its spin should not affect the spectrum of gravitational waves released, so I didn’t mention it for this bite! If you want to read more about when gravitational waves are released, there is an excellent overarching astrobite on the topic here!