Title: Discovering the QCD Axion with Black Holes and Gravitational Waves
Authors: Asimina Arvanitaki, Masha Baryakhtar, Xinlu Huang
First Author’s Institution: Perimeter Institute for Theoretical Physics, Waterloo, Ontario N2L 2Y5, Canada
Status: : Published in Phys. Rev. D 91, 084011 (2015), open access on arXiv
The success of the LIGO/VIRGO collaboration has opened a window into many previously gravitationally unprobed phenomena, from tiny dark matter candidates to supermassive black holes. One such example is black hole superradiance: when a wave is scattered off a rotating black hole, it can exit with a larger amplitude than it had before, carrying with it some of the angular momentum of the black hole. This effect is particularly interesting in the case of bosonic waves, whose quantum numbers are not suppressed by Pauli’s Exclusion Principle. This interaction leads to the formation of high occupation bound states around the black hole – creating, in essence, a gravitational atom, with the black hole as its nucleus.
Thus, black hole superradiance can be used to detect signals of bosonic fields which cannot be observed in a detector. In this paper, Arvanitaki et al. consider in particular the QCD axion, a robust bosonic dark matter candidate, and the signatures it might produce through black hole superradiance. They estimate its gravitational signatures, both from transitions between “orbitals” of the gravitational atom and from annihilation, as well as its bounds from black hole spin measurements. Both of these criteria are measurable by advanced LIGO (aLIGO), and future observations will serve to constrain axion masses in the event of no detection.
Gravitational Atoms
Just like the familiar and beloved Hydrogen atom, the gravitational atom has a nucleus – in this case, the black hole – and a cloud of surrounding matter arranged in orbitals. Rather than electrons, however, here the orbiting matter can be any boson. The boson isn’t required to be dark matter, nor is it even required to come close to the black hole: superradiance can start even via a quantum mechanical fluctuation in the vacuum. In order for this to happen, the superradiance condition must be satisfied, where
is the angular velocity of the boson divided by its angular momentum with respect to the black hole’s rotation axis, and
is the angular velocity of the black hole at the Schwarzschild radius. This is analogous to throwing a ball at the edge of a spinning cylinder: if the ball is moving slower than the cylinder is spinning, it’ll bounce off with a little added velocity.
Once superradiance starts, the occupation number of the bosonic cloud grows exponentially – unlike a Hydrogen atom, which has only a single electron. Nevertheless, we can index the orbitals with the usual quantum numbers , with occupation levels which grow at a rate set by the mass of the black hole. These occupation levels will grow until the boson cloud extracts enough angular momentum from the black hole that the superradiance condition is no longer satisfied. This growth can last a long time, since superradiance timescales are billions of times shorter than the evolution timescales of black holes, which can take years. The relevant superradiance timescales are illustrated in Figure 1.
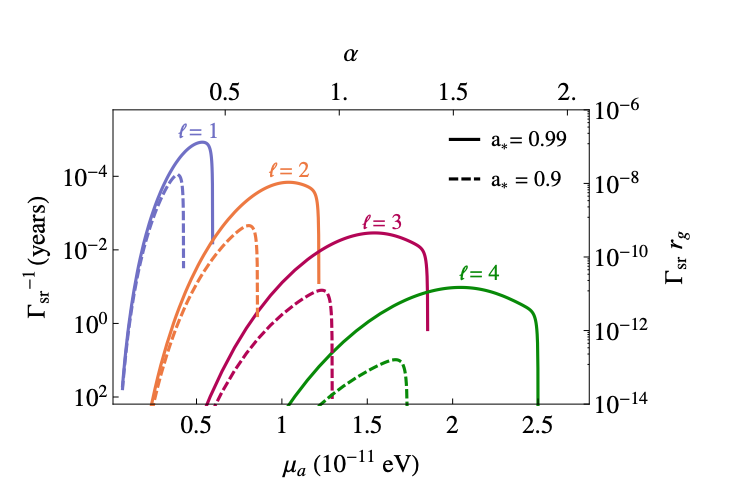
Figure 1: Superradiance timescales in terms of orbital levels left to right, with
and
. Two types of lines represent different spin parameters
, where
is a maximally spinning black hole and
is one without any spin (see this bite for more discussion). The solid lines represent black hole spin parameter of
, and the dashed lines represent a slightly lower spin value of
. The bottom axis represents the mass of the axion boson. These particular orbital examples are chosen due to their relatively short growth times, represented on the left axis as the corresponding timescale to exponentially increase boson occupation numbers in the given orbital. The right axis represents the dimensionless rate of accretion multiplied by the gravitational radius of the black hole,
, as a function of the gravitational coupling between the black hole and the boson,
. Figure 1 in the paper.
Black Hole Spin-Down
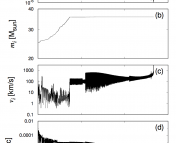
During this time the black hole is continuously spinning down due to the extraction of angular momentum by the bosons, which causes the bosonic cloud to transition from one orbital to the next, and finally stop being affected by superradiance completely. An example of such an evolution is presented in Figure 2. Superradiance is easily triggered, even without the immediate proximity of a bosonic field, and proceeds to grow the bosonic occupation number exponentially. We expect to detect an ensemble of preferentially lower-spin black holes in the universe if any bosonic field exists. As LIGO and, in the future, LISA detect more binary mergers and place stricter bounds on the spins of the resultant black holes, a statistical sampling of black hole parameters will serve to set bounds on the masses of all bosonic particles, in particular axions.
Furthermore, because superradiance isn’t sensitive to any other particle parameters, this comparison can serve to exclude any bosonic fields at a given particle mass, providing a powerful probe of an otherwise inaccessible parameter space.
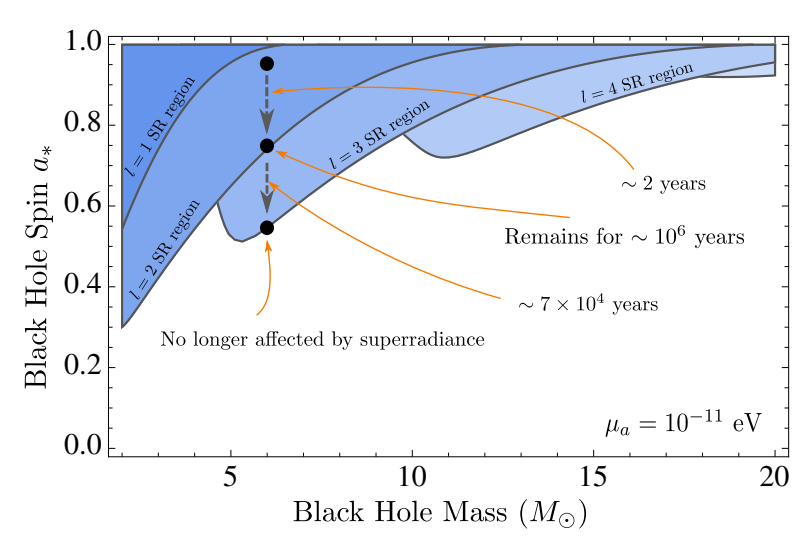
Figure 2: Spin-down of black holes due to superradiance. For a given boson mass , a choice of black hole mass and spin is presented with the topmost point. Starting in the
, it would take such a black hole 2 years to spin down to the l=3 orbital via superradiance. It would remain on at that spin for
years, before spinning down further for
years, after which it would no longer be affected by superradiance. Figure 2 in the paper.
Gravitational Signals of Axions
A more direct way to look for signatures of axions is through their own monochromatic gravitational signatures. One source of such a signature is the transition of bosons between orbital levels; another, the annihilation of two colliding bosons. These are particularly promising since both signals will be significantly enhanced: transition signals are multiplied by ,where each
represents the occupation number of the initial and final states, and annihilations are enlarged by $$.
Each signal will dominate at a different stage in the gravitational atom’s lifetime. For instance, transitions will be the dominant gravitation signal of the bosons when there are at least two levels with significant boson occupation numbers present. In Figure 2, this might happen on the to boundary, and last for a million years. On the other hand, annihilations will dominate when only one level has significant occupation numbers: for example, in the orbital in Figure 2, lasting for almost 70,000 years.
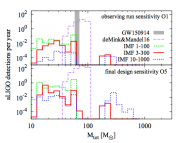
Figure 3 shows the expected frequency and strain of some allowed orbital transitions. With aLIGO’s current sensitivity of and frequency range of , several of these are viable detection targets. Furthermore, the launch of LISA (expected in 2034) will open another window in the frequency range, allowing for even more targets for detection. Thus, this project is not yet complete, but will be ongoing for years to come. Along with statistics on black hole spin down, these aLIGO targets will serve to either detect axions or constrain their mass, turning gravitational atoms into novel and exciting dark matter laboratories.
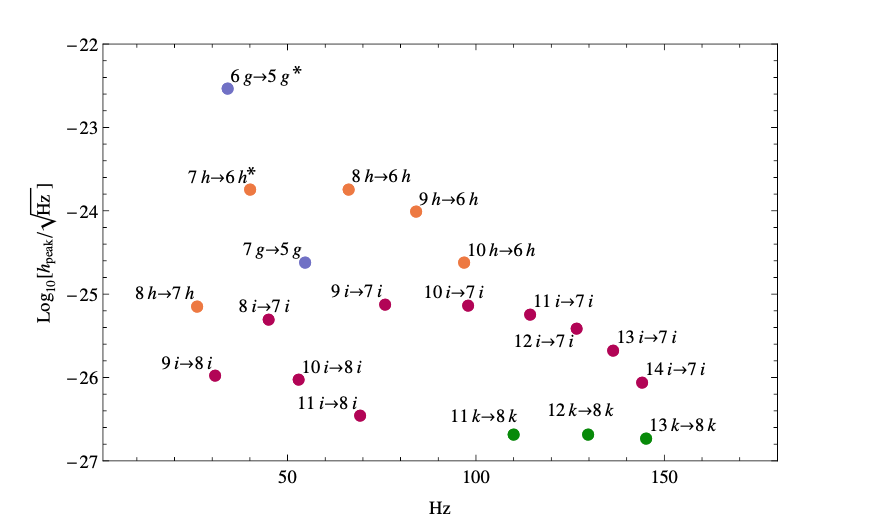
Figure 3: Expected gravitational strain and frequency of signal from allowed orbital transitions. The mass of the black hole is with spin
; the system is assumed to be
away and the signal integrated over
. Note that
and
are starred because they fall within an interesting range that is within aLIGO’s observational window. These transitions’ convenient frequency range will allow future aLIGO data to put robust constraints on the existence of various bosonic fields, or otherwise detect them! Figure 4 in the paper.