When photons talk to each other

• Title: Implications of automatic photon quenching on compact gamma-ray sources
• Authors: M. Petropoulou and A. Mastichiadis
• Institution of first author: Department of Physics, University of Athens, Greece

Photon pair-production

When an electron and positron meet each other, they annihilate to produce to gamma-rays. The reverse of this process is also possible – if a gamma ray with energy ϵ_γm_ec² meets another photon with energy ϵ₀m_ec² such that ϵ_γ ϵ₀ ≥ 2 , then an electron-positron pair is produced. For any gamma-ray emitting source, such as a blazar or gamma-ray burst, that also contains some target soft photons, this process sets an upper limit to the “compactness” (ratio of gamma-ray luminosity to size)*. For sources more compact than this limit, the source is optically thick to its own gamma-rays.

Critical Magnetic Field

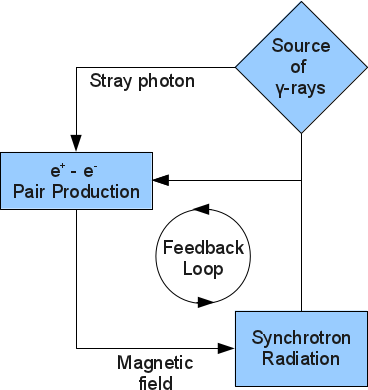
Even in the absence of an external source of photons, another mechanism can produce soft photons that can gobble up gamma-rays: synchrotron radiation from pair-produced electron and positrons. While this requires the presence of a magnetic field, only a single stray photon is needed to make a bunch of intense gamma-rays unstable and lead to a runaway pair production.

The requirement that the synchrotron photon be sufficiently energetic for pair production, leads to a condition for a minimum magnetic field:
with Here is the energy of the γ-ray.

This requirement is easily satisfied by parameters derived from modeling sources, such as 3C279.

The authors study this feedback loop in detail, first analytically and then numerically. They make the basic assumptions

1. Spherical source of size, R
2. Tangled magnetic field of strength, B
3. Mono-energetic gamma-rays, with energy E_γ = ϵ_γm_ec²
   (later relaxed to include power-law gamma-ray injection)
4. Constant gamma-ray injection rate, with luminosity, L_γ^inj.

Critical γ-ray “compactness” (∝ L_γ^inj/R) as a function of gamma-ray energy, when (i) σ_γγ and synchrotron emissivity are approximated by a step- and a δ- function respectively (lower curve: analytic calculation; points: numerical verification) and (ii) when for both quantities the full expressions are used (upper curve – numerical only). Figure 3 from the article.

Analytical Argument: Marginal Stability
Assume that the γ−rays pair-produce on some soft photon and that the created electron-positron pairs cool by emitting synchrotron photons. Now, an electron emits several synchrotron photons before cooling completely, so if the number density of the γ−rays is such that at least one of the synchrotron photons pair-produces on a γ−ray, then the system is critically balanced. This leads to a condition on the gamma-ray luminosity of the source:

where is the Thomson cross-section.

This critical ratio of L/R is called the critical “compactness”,

Kinetics

To solve the full time-dependent problem and to deduce equilibrium solutions, the authors try both

• Analytical techniques, assuming simple forms for
  1. the photon pair-production cross-section (δ-function, step function)
  2. the synchrotron emissivity (δ-function)
• Numerical calculations,
  • First verifying the analytic estimates, and then
  • Including more complex physics – synchrotron self-Compton radiation and synchrotron self-absorption.

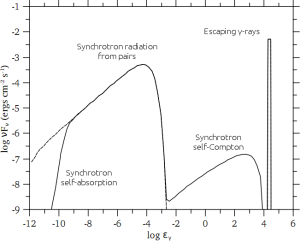
Synthetic Spectrum

Using their model, the authors are able to produce a synthetic spectrum for a gamma-ray source.

1. The spectrum contains a high-energy peak corresponding to the fraction of the gamma-rays originally injected by some unknown process in the source, which are able to leak out without pair producing. The SED of this component is the injection spectrum (assumed to be a δ-function or a power law).
2. Next, there is the synchrotron emission from the pair-produced electrons and positrons (the strength of this component depends on the magnetic field). This component peaks in the X-rays.
3. Third, this synchrotron radiation is self-absorbed below some frequency (i.e. optically thick), which leads to a sharp cutoff at low frequencies
4. Finally, there is a small bump at high energies from synchrotron self-Compton – the electrons/positrons scattering their own synchrotron radiation to high energies.

Synthetic Spectral Energy Distribution for a compact gamma-ray source, with a δ-function gamma-ray injection spectrum. Figure 5 from the article (annotated by Tanmoy Laskar).

SED of quasar 3C279, with photon pair production models overplotted. Figure 11 from the article.

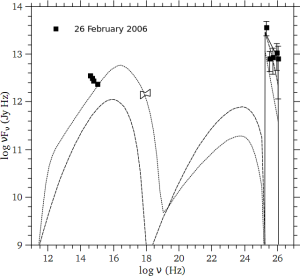
Comparison to Observations

By plotting gamma-ray and X-ray flux measurements of the quasar 3C279, the authors are able to use their model to constrain the magnetic field in the source, its Doppler factor (assuming the source is beamed towards us) and its size.