- How Important is the Dark Matter Halo for Black Hole Growth?
- Marta Volonteri, Priyamvada Natarajan, & Kayhan Gultekin
- First and Third Authors: University of Michigan, Second Author:Yale University & Harvard-Smithsonian Center for Astrophysics

NGC 5128 is is just one of many galaxies thought to harbor a super-massive black hole at its center. (nasa.gov- an ESO PR Photo in June 2003)
Look into the heart of almost any galaxy in the universe and there you will find a monster. Observational evidence has shown that many of the galaxies in our local universe exhibit a bulge containing a super-massive black hole (SMBH) that is typically millions (sometimes billions) of times the mass of our sun. Now, this SMBH is incredibly massive, but its gravitational influence does not reach very far out into the galaxy. It was curious, then, when astronomers realized that there is a significant correlation between the mass of the SMBH and σ, the velocity dispersion of the galaxy’s bulge. A newly debated idea is whether or not the mass of the SMBH correlates with the dark matter halo of its host galaxy. As a review, galaxies are thought to be made of mostly dark matter that is distributed in a Navarro-Frenk-White profile. Both these correlations suggest co-eval growth of the SMBH and the stellar component likely through regulation of gas supply in the nucleus of the galaxy. This paper re-examines recent work that has argued that SMBH masses do not appear to correlate with galaxy disks and it is the morphology, not the dark matter halo, which determines whether a correlation exists.
To get straight to the point, the authors argue that the reason the super-massive black hole (SMBH) and mass of the dark matter halo seem to show a strong or weak correlation is a direct consequence of the role of galactic mergers or lack there-of. Major mergers between galaxies can trigger both SMBH accretion episodes and star formation. These train wrecks occur much more frequently for massive galaxies (halos) at high redshift, while low mass galaxies (halos) experience practically no major mergers during any cosmic epoch. If mergers are able to simultaneously grow both the stellar population and the mass of the SMBH, we should observe a tight coupling between these two components in the nucleus of only the most massive halos.
Because we can’t directly measure dark matter mass, we use the circular velocity of the galaxy to infer an interior halo mass (which is mostly dark matter). The authors look at a sample of 25 observed galaxies where these properties have been measured. This same sample was used by another group who settled on the conclusion that there was no significant correlation between the mass of the SMBH and the circular velocity (halo mass). What the authors here find is that there is indeed a correlation with much of the scatter in the relation occurring at the low mass end for the SMBH. In a previous paper, Volonteri found that low mass bulge-less galaxies today are unlikely to host nuclear black holes and that the relevant host galaxy property is the halo’s spin for “seeding” (creating) SMBHs through direct collapse. Joshua wrote a recent astrobite about “seeding” black holes. Currently, theory predicts only certain conditions where these can form at high redshift. If you are interested, check out page 3 of the paper for a description of these constraints.
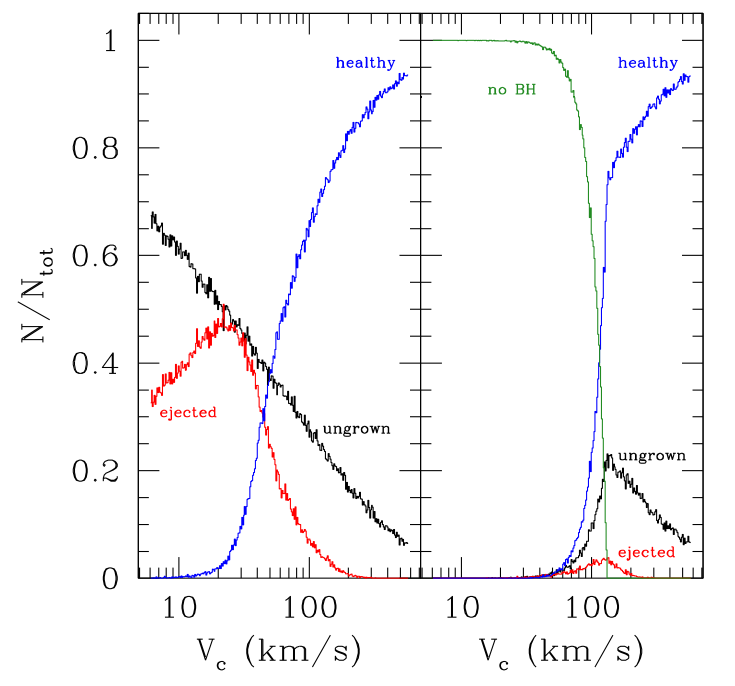
Figure 2: "Distribution of SMBH growth histories as a funtion of halo mass." -Volonteri The left panel is if all galaxies are seeded with a SMBH and the right panel uses an "occupation fraction".
Nowadays, the way astronomers see if they really understand what is being observed is by simulating it. The authors do exactly this by running a Monte Carlo simulation of the growth of 560,000 galaxies and see how many SMBHs are “ungrown” (no major mergers), “ejected” (kicked because of gravitational recoil), or “healthy” (at least one major merger brought the SMBH on the correlation). See another of Joshua’s astrobites about SMBHs that have been kicked during mergers. They assume that initially each halo hosts a SMBH and the halo mass is predicted by the mass of the black hole – circular velocity relation that is proportional to the halo mass to the 4/3 power. With a variety of other necessary assumptions (see paper), the authors present their distribution of SMBH growth histories in Figure 2 here (Fig. 3 in the paper). The most obvious thing is that there are different regimes. If the circular velocity is greater than 100 km/s, it has experienced at least one major merger. If the assumption holds that these major merger events bring the SMBH on or near the expected relation with circular velocity (halo mass), then these SMBHs are “healthy”. As mentioned before, much of the scatter in the relation occurs toward lower masses which is exactly where the authors find most of the SMBHs either “ungrown” or “ejected” in their simulation. Also note that ejections happen more often in intermediate sized halos because low mass galaxies have few mergers (disruptions) and large galaxies have high escape velocities making ejections more difficult.
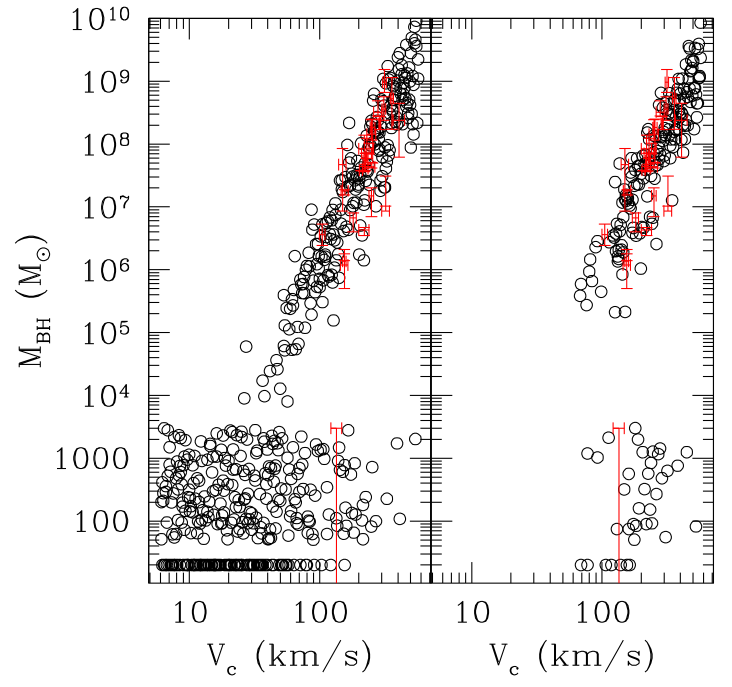
Figure 3: Circles represent SMBH-circular velocity relations in the Monte Carlo simulations. The red lines are the 25 observed galaxies and their relation. The left panel is if all galaxies are seeded with a SMBH and the right panel uses an "occupation fraction".
In Figure 3 (Fig. 4 in paper) the authors show their predicted mass of black hole – circular velocity (halo mass) relation for their Monte Carlo sample overlaid with the 25 observed galaxies. To arrive at their black hole masses they assume that every major merger increases the SMBH mass by where Δ is normally distributed about 0 with a standard deviation of 1. This is only for “healthy” SMBHs. They set a different mass for “ungrown” SMBHs which, remember, is the case for galaxies who don’t undergo major mergers. A nice comparison can be seen between their simulated relation and that of the observed data.
In conclusion, the authors propose that dark matter halos are important in the overall formation and growth of black holes when you consider that the probability that one will undergo a major merger is dependent on the halo mass. If this is the process by which the relationship is set between the two masses, then a weaker or non-existent correlation is expected for low mass systems which is what is seen in observational data.



Trackbacks/Pingbacks