- Title: Cold Gas Flows and the First Quasars in Cosmological Simulations
- Authors: T. Di Matteo, N. Khandai, C. Degraf, Y. Feng, R.A.C. Croft, J. Lopez, V. Springel
- First Author’s Institution: McWilliams Center for Cosmology, Carnegie Mellon University
As Nathan mentioned a couple weeks ago in this astrobite, the recent discovery of a z ~ 7 quasar has added some serious new constraints to theories about the growth of supermassive black holes in the early universe. A quasar that bright at that redshift implies that theorists need to figure out how to grow billion solar mass black holes in a relatively short span of time – just 750 million years after the big bang. Not surprisingly, cosmological simulations of the early universe are one of the largest areas of theoretical research in astronomy at present, and the authors of today’s paper claim that they have built a simulation which can easily reproduce these hulking black holes in just a few hundred million years.
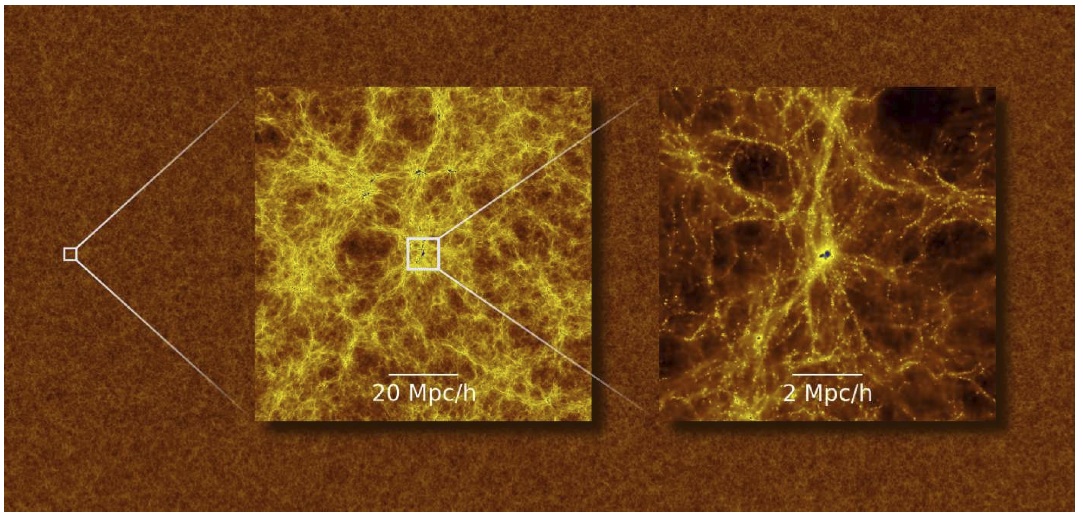
The simulation, called MassiveBlack, covers a giant region of space at very high resolution, with 65 billion particles in a cube that is 0.75 Gpc on each side. This allows the authors to investigate a cosmological region containing many dark matter halos large enough to contain supermassive black holes, while at the same time probing the much smaller scale galactic physics within each halo, such as star formation, black hole accretion, and quasar feedback processes. The simulation is run from a time shortly after the big bang to redshift 5, probing the cosmological timescale over which supermassive black holes need to form to be consistent with observations. A two-dimentional “unwrapped” view of the simulation volume at z = 5 is shown in the figure below. As expected, the region looks fairly homogenous over large scales, but as one zooms in, individual halos containing massive black holes can be seen.
The results of the simulation center on an important fact – in order for the seed black holes to grow to several billion solar masses by z ~ 6, they need to be fed by filaments of cold, dense gas streaming into each halo. The idea that galaxies and black holes are fed by these filaments of cold gas is called “cold flow accretion”, and though some astronomers claim to have seen observational evidence for it at low redshift (see this astrobite), it remains primarily a theoretical claim. Using MassiveBlack, the authors zoom in on several of the growing supermassive black holes in a series of redshift snapshots, and they analyze not only the mass of the black holes, but also the gas density and temperature around them (see the figure below). Sure enough, each quasar is fed by two or three streams of cold, dense gas. Importantly, feedback from the quasar does not begin to heat the surrounding gas enough to disrupt the streams until after a redshift of about 7, by which time the black holes are already large enough to satisfy observational constraints. Once the feedback does kick in, the black hole growth stops being exponential, and begins to self-regulate.
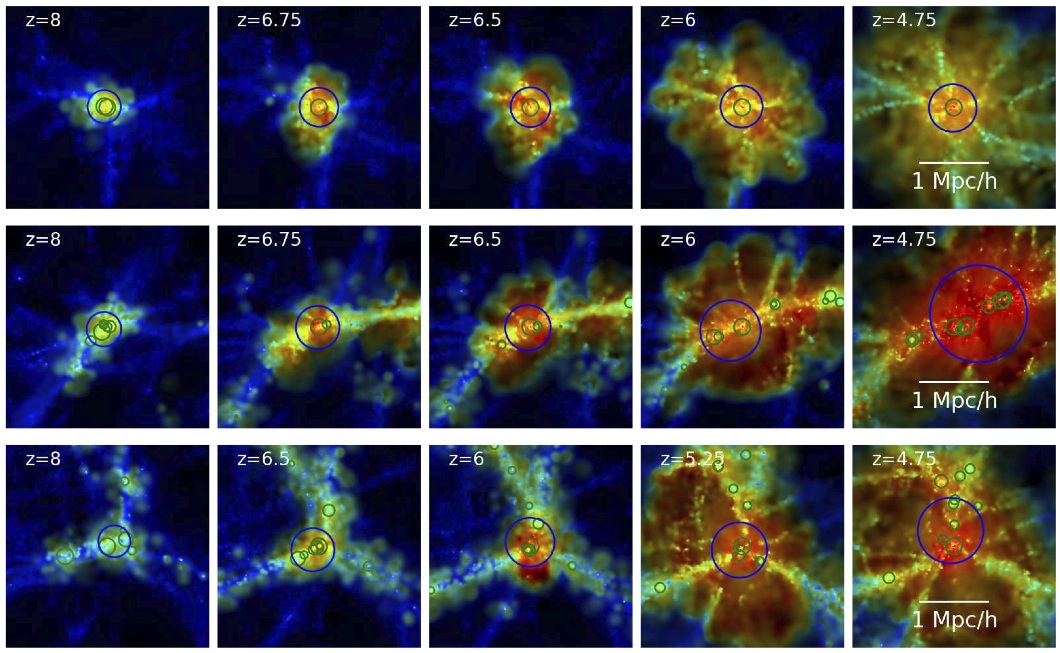
Shown here are three examples of the supermassive black holes typical in the simulation, with redshift evolution from left to right. Green circles indicate black holes, while blue circles highlight the virial radius of each halo. The gas temperature is indicated by the color scale, with the coldest gas in blue, and the hottest in red.
The authors make another important point in their analysis. Mergers, a competing theory for early supermassive black hole growth, play a relatively small role in the early redshifts probed by this simulation. They become more important later, for galaxy growth, but the black holes are growing so quickly that they do not have time to undergo very many significant merging events. This leads the authors to a testable hypothesis. The black holes attain their giant, several billion solar mass sizes within a few hundred million years, while the growth of their host galaxies is expected to proceed much more slowly, on scales of a few billion years. This means that these early quasars should represent significant deviations from the MBH-σ relation (discussed in this astrobite), since the black hole growth is far outstripping the host galaxy growth.




Does all of the gas from the cold streams reach the MBH or can some of it remain in the disk, if for example it comes with sufficient AM? and then the host galaxy will also grow at a comparable rate?
Good question! Unfortunately, this paper didn’t go into much detail on that point, beyond the fact that enough gas reached the black hole to keep accretion going at the Eddington rate. Perhaps followup papers will provide the answer.
What I have seen in other work is that star formation is strongly linked to cold gas accretion (see e.g. http://arxiv.org/abs/1102.3912). I would therefore expect that a lot of the cold streams also just join the ISM of the galaxy and then might either take part in star formation or black hole accretion.
I agree, that seems quite probable, but since it wasn’t addressed in the paper, I wouldn’t want to imply that is the author’s opinion.
Thanks. I assume you have experience in analyzing AMR simulations outputs. I would appreciate if you could answer some general questions: regarding the figures in your thesis “Nature and Nurture in Galaxy formation simulation”, were they done in SM, python or IDL?
Second, Regarding simulation outputs, for example the gas density, to make the density projections of the halos you show in the thesis(figure 2.1) do you interpolate the density data on a grid and then project the data from a grid or do you use a different way?
Thanks.
@Evan: indeed, that’s why I said I had seen it in other work 🙂
@Mark: All images and plots in the thesis are made with IDL (although I now made the transition to python, or rather: I am making the transition :)). The simulations I used were SPH, not AMR. In order to make the density renderings I just calculate the density in the center of every pixel. It is done using all particles that you want in the box, projected on the image plane, and calculating their contribution to the density in that point (the pixel center) in a way consistent with the SPH formalism. It could be done easier, for example, just adding up all particles that end up in the pixel, dividing by its ‘volume’. Some methods are faster, other methods are more accurate. For illustration purposes speed is probably the relevant criteria, while for science a case could be made for slow, but accurate methods. I’d be happy to discuss these issues further if you want, but let’s do that offline. Just send me an email, the address should be available here. If not: the fact that you found my thesis probably means you can find my email addy too 😉
Note that this paper will be the topic of the Twitter astronomy Journal club (http://astrojournalclub.wordpress.com/) next Thursday! So if you are interested in this paper feel free to join the discussion on Thursday July 28th 2011, 19:00 UT, using #astroJC.