- Title: Life might be rare despite its early emergence on Earth: a Bayesian analysis of the probability of biogenesis
- Authors: David S. Spiegel & Edwin L. Turner
- 1st Author’s Institution: Dept. of Astrophysical Sciences, Princeton University
In yesterday’s post, Dan gave us a great summary of why statistics are important to astronomers. Conveniently, today’s paper provides a concrete example of astronomers using one of the methods Dan described yesterday, Bayesian statistics, to try to answer the question: just how frequently should we expect extraterrestrial life to emerge?
As more and more astronomers try to answer this question empirically (i.e., by discovering habitable planets, and ideally, their inhabitants), the authors of this paper decided to try a complementary theoretical approach. In order make a statistical estimate of the abundance of extraterrestrial life, they needed to come up with the probability of abiogenesis per unit time and per unit volume; as a function of physical and chemical conditions in a pre-biotic environment. In other words, they say, perhaps if we can estimate the probability of life emerging in favorable conditions, then using the number of these habitable environments (presumably from exoplanet surveys), we could estimate the frequency of extraterrestrial life.
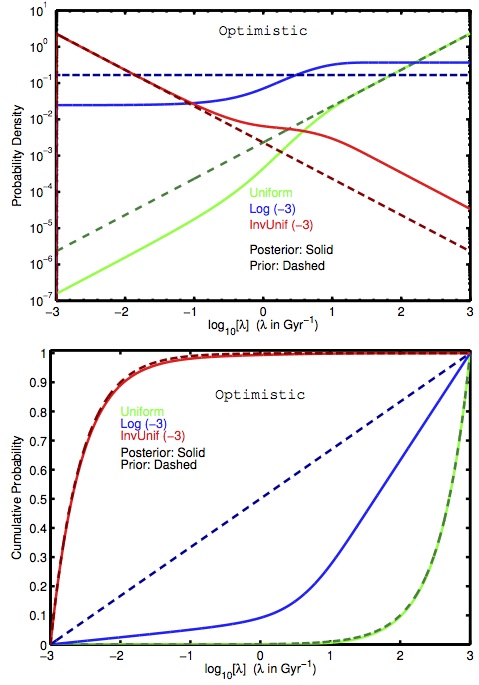
This figure shows the "Optimistic" model, one of three tested in the paper. Different colors correspond to different functional forms of lambda, while solid and dashed lines correspond to the posterior and prior probabilities, respectively.
Enter Bayes’ Theorem, which can be written as: P[M | D] = P[D | M] x Pprior [M] / P[D], where P denotes a probability, M is a model, and D is data. This theorem states that the “posterior probability” of a certain model, given some data, P[M | D], can be derived using a likelihood term, P[D | M]; a prior term, Pprior [M]; and the marginal probability of the data, P[D]. To use this theorem, the authors needed to define a “probability of abiogenesis” (the probability of life emerging). They therefore specify a term, λ, which is the probability per unit time of life evolving. Most previous studies on this subject have suggested that λ is probably not small, because then it would be surprising for life to have arisen on Earth as quickly as it did. This paper’s authors point out, however, that while the time-span between Earth achieving suitable pre-biotic conditions and the arrival of life is a basis for estimating λ, we necessarily find ourselves in a situation with a small λ (that is, a quick rate of biogenesis), because if life had taken a long time to emerge on Earth, we would not yet have evolved to the point of being able to think about it!
The authors decide to treat λ, the probability per unit time of life developing, as a Poisson process. The probability of life arising in a time t can then be defined as 1 minus the probability of it not arising: Plife = 1 – PPoisson[λ, 0, t ] = 1 – e – λ (t – tmin) . This equation can then be used as the model in Bayes’s Theorem. The model assumes a tmin and tmax outside of which life cannot form, which puts further constraints on the probability of life arising. tmin is the time it takes for a recently formed planet to achieve suitable pre-biotic conditions, while tmax is the time after which life can no longer survive on a planet, probably around 10 Gyr for planets around main sequence stars like our sun.
An interesting point: The Minimum Evolutionary Time Constraint
We see that life arose relatively early on our planet, therefore we might assume that λ is large. However, it took almost 4 Gyr for organisms capable of pondering this fact to evolve. If that amount of time is usually necessary for such sentient beings to evolve, then we HAVE to find ourselves on a planet on which life arose relatively quickly, otherwise we would not yet exist. This, the authors point out, is independent of the value of λ. To account for this, the authors introduce another variable into their analysis, δtevolve. See the paper for figures showing the effect of δtevolve.
Results
The authors consider three different functional forms for λ: one which is uniform in λ, one which is uniform in λ-1 (the mean time until life appears is uniformly distributed), and one which is uniform in log10λ. They also investigate several different models; the one shown in the figure to the right is their “Optimistic” model, in which life emerged on Earth within 0.2 Gyr of tmin, and had 3 Gyr to evolve. The figure shows the effects of the prior and λ on the probability density function (PDF), and the cumulative distribution function (CDF). In essentially every model, the authors find that the posterior probability (the probability of life elsewhere in the the universe) is strongly dependent on our prior knowledge (as shown by the fact that the solid lines closely follow the dashed lines in the plot) and the value chosen for λ. If a very low value is chosen for λ, the probability of extraterrestrial life is very low, and if a high value is chosen, the probability is high. Thus, they conclude that “A Bayesian enthusiast of extraterrestrial life should be significantly encouraged by the rapid appearance of life on the early Earth but cannot be highly confident on that basis.” Interestingly, the authors also note that if we were to discover definitive proof that life once arose on Mars, the posterior probability of low λ would be greatly reduced. A detailed plot of the effects of life on Mars (or lack thereof) on the probability of extraterrestrial life is also included in the paper.



Trackbacks/Pingbacks