Two papers appeared on the arXiv recently that combine data from the Kepler exoplanet transit survey and two different radial velocity surveys (the M2K survey for the first paper and HARPS for the second) in order to determine the mass-radius relationship of small exoplanets. What is the nature of the smaller candidates discovered by the Kepler mission? Are they rocky super-Earths, gaseous mini-Neptunes, or a heterogeneous mix of both rocky and gaseous planets? Both of the recent papers do an excellent job of addressing this question, so I decided to feature two papers on astrobites instead of choosing between them. The first paper is described below and the next paper will be described in my next post.
The First Paper
(posted Tuesday, August 30)
- Paper title: On the Nature of Small Planets around the Coolest Kepler Stars
- Authors: Eric Gaidos, Debra A. Fischer, Andrew W. Mann, Sebastien Lepine
- First author’s affiliation: Department of Geology and Geophysics, University of Hawai’i at Mānoa, Honolulu, HI
The Second Paper
(posted Wednesday, August 31)
- Paper title: Combining Kepler and HARPS Occurrence Rates to Infer the Period-Mass-Radius Distribution of Super-Earths/Sub-Neptunes
- Authors: Angie Wolfgang, Gregory Laughlin
- First author’s affiliation: Department of Astronomy and Astrophysics, University of California, Santa Cruz, CA
Background
Several previous astrobites have explained the various ways to detect exoplanets. The two most successful methods are the radial velocity method and the transit method. The radial velocity method infers the presence of a planet based on the periodic Doppler shift induced in the host star’s spectrum due to the gravitational tug of the planet on the star, while the transit method identifies planets by periodic dips in the brightness of the star as the planet passes between the host star and the observer.Since more massive planets exert a stronger tug on their host star, radial velocity surveys are most sensitive to massive planets. Similarly, transit surveys are more sensitive to larger planets than to smaller planets because a larger planet blocks a greater fraction of the host star’s disk and causes a larger decrease in brightness. Due to the difficulty of detecting either small planets or low-mass planets, most small planets have either measured radii or measured masses, but not both. To make matters even more difficult, the inclination of most radial velocity planets is unknown, so the actual mass of the planet could be much larger than the mass calculated by assuming that the planet lies in the same plane as the observer.
Because most planets do not have both measured masses and radii, astronomers must conduct a statistical analysis of the RV sample and the transit sample in order to determine the relationship between exoplanet radius and mass. As radial velocity and transit surveys improve, astronomers will increase the sample of exoplanets with both measured radii and measured masses, but for now most researchers make the assumption that the RV-detected planets and the transit-detected candidates are drawn from the same distribution of planets and should therefore obey the same relationship between mass and radius.
The First Paper: Gaidos et al. 2011
This paper compares the Kepler candidate list to the 172 indications of planets detected by the M2K survey of relatively quiet late K and early M dwarfs. Because many of the Kepler candidates orbit hotter stars, Gaidos et al. choose to restrict their analysis to only the Kepler and M2K stars with effective temperatures between 3660 K and 4660 K so that they are considering planets orbiting stars with similar temperatures in each sample.
Converting Radii to Masses
Gaidos et al. define a mass-radius relation to convert the radii of the Kepler candidates into masses. Since many large transiting planets have both measured radii and measured masses, Gaidos et al. use the mean densities of the 120 large transiting planets with RV measurements to predict the densities of the large Kepler candidates. They then use those densities to calculate the masses of all of the Kepler candidates with radii larger than three Earth radii.
For the smaller planets, Gaidos et al. use a simple power law scaling so that the planet mass increases with radius as M=Rα, where the power law index α depends on the interior structure of the planet. A steep power law index would indicate a population of rocky planets (e.g., α~3.85 for planets with roughly the same composition as the Earth), while a shallower power law index (α=2 or even flatter) would describe a population of gas-rich planets. In the first half of the paper, Gaidos et al. assign the same value of α (and thus the same composition) to all of the small planets in order to determine the best fit value of α for a homogeneous population of small planets, but they later consider whether a mixture of mini-Neptunes and Super-Earths could account for both the Kepler and M2K data.
Comparing to the M2K Survey
After assigning masses to all of the Kepler candidates, Gaidos et al. conduct a Monte Carlo simulation in which they assign the Kepler candidates to target stars from the M2K survey. The planets are given random orbital inclinations and the probability that each Kepler candidate is assigned to the star is set by the occurrence rate that Gaidos et al. derive for each candidate. Gaidos et al. then compute the expected RV signature from each planet and apply Kolmogorov-Smirnov (K-S) and the two-sided Kuiper test to compare the distribution of the root mean square (RMS) RV for the model population to the RMS RV distribution from the M2K survey.
Both the K-S test and the Kuiper test are useful ways to determine whether two populations are drawn from the sample distribution. The K-S test indicates the maximum difference between the cumulative distributions of the two samples, so it is most sensitive to differences near the median of the distribution. Accordingly, the K-S test is often used in conjunction with a Kuiper test, which measures how well two samples agree in the tails of the distribution. The figure below displays the K-S probability that the modeled RMS RV are drawn from the same distribution as the observed RV variations as a function of the intrinsic stellar variability (“jitter”) and the power law index α. The K-S probability is maximized for high values of α, which suggests that the small planets are more likely to be rocky than gaseous.
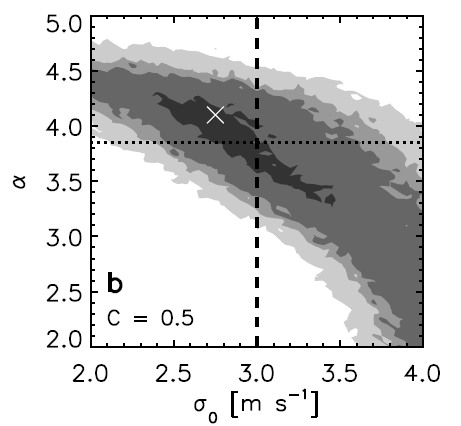
The Kolmogorov-Smirnov probability that the modeled distribution of RV variations is drawn from the same distribution as the RV variations observed by the M2K survey. The x-axis is the "jitter" (stellar noise) and the y-axis is the power law index describing the mass-radius scaling relationship. Steeper values of alpha correspond to rockier planets while lower values of alpha indicate gaseous planets. The vertical line indicates the current estimate for the maximum amount of jitter in the stellar sample and the horizontal line marks the value of alpha that corresponds to an Earth-like mass-radius relation. The contours indicate K-S probabilities of 0.01 (lightest), 0.05, 0.1, and 0.5 (darkest) and the "X" marks the alpha and jitter corresponding to the maximum K-S probability. Figure 5b from Gaidos et al. 2011.
In this case, the Kuiper test agrees with the K-S test and Gaidos et al. find that the observed distribution of RMS RV for the M2K survey is best fit by a population of primarily rocky Super-Earths rather than by a population of gaseous mini-Neptunes. Gaidos et al. also report that the observed radii and masses could also be explained by a heterogeneous mix of rocky planets and gaseous planets if the majority of the small planets are rocky.


Great post! I was hoping someone would parse out this paper for me (Gaidos et al). Thanks for the good explanation.
Thanks, Adele. I’m glad you enjoyed the post.