Paper title: Smoothed Particle Hydrodynamics: Things I wish my mother taught me
Author: D. J. Price
Author’s Affiliation: Monash Centre for Astrophysics (MoCA), School of Mathematical Sciences, Monash University, Vic 3800, Australia
The title of this article caught my eye on the arXiv for two reasons: rarely do authors mention their mother in a paper, and like the author I also wished that my mother (or anyone) had taught me about smoothed particle hydrodynamics. The author soon clarifies that actually it was his PhD supervisor, not his mother, who he wishes had taught him the important details related to simulations, so in fact the rest of the paper pays no further attention to family ties. But, the subject of smoothed particle hydrodynamics (SPH) still fascinates me, and seems to be extremely relevant to current astronomy, so I will summarize the topic here. I should also make the disclaimer that I have never used SPH, so what I present is merely what I have learned from reading the paper.
Fundamentals:
SPH is a computational method used to model flows, and it is used in a variety of subjects including astrophysics and oceanography. It begins with a known distribution of point-mass particles, and computes density such that density is independent of the following particle characteristics: (1) the absolute positions of the particles, (2) arbitrary rotations, and (3) histories of the particles. Summing up the density comprises what the author calls the fundamental axiom of SPH, as it use discrete particles of fixed mass to describe fluid properties. The resolution of the method (or the smallest step-size that one can take) depends on the particle mass since density can only go up or down by adding or subtracting a discrete number of particles. Because the particles cannot lose or gain mass, then the total mass is a conserved quantity.
What else can you learn from SPH:
From the density sum, based on the masses of particles, one can find kinetic minus thermal energy (called the Lagrangian), and then get the equations of motion for each particle (shown as a form of the Euler equation). The majority of the paper describes the key features of SPH, which are:
- A solution to the continuity equation (quantities are conserved locally)
- Advection (transport in the same direction as the fluid flow) of mass and other fluid quantities
- Zero intrinsic dissipation (i.e. energy can’t escape)
- Conservation of mass, momentum, angular momentum, energy and entropy, which the author notes are very important for astrophysics
- Minimum energy state for particles (a.k.a. the “grid” of particles in the natural state of the system
- Resolution that follows the mass

Special consideration must be taken to ensure that quantities are conserved properly, and if not, the final particle distribution will be affected.
Summary:
What is SPH good for? Simulating situations that follow mass, such as astrophysical problems of gravitational collapse in the formation of stars or cosmological structure. While the paper does not go into the details of how to generate an SPH code, which the author claims can be done simply in a few days, it does a nice job of explaining some of the capabilities of SPH. In fact, its alternate subtitle is “When you should, when you shouldn’t”. Interested to learn more details? You can find several other astrobites posts on the topic.


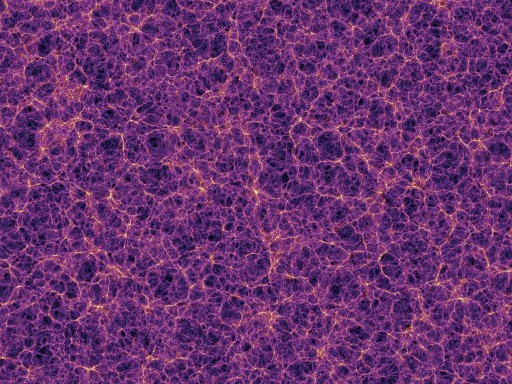
Among the previous Astrobites posts Adele linked to, be sure to check out Nathan Goldbaum’s excellent posts on how to use the Gadget software in particular. These walk you through the steps to perform your very own SPH simulations:
http://astrobites.com/2011/04/02/installing-and-running-gadget-2/
http://astrobites.com/2011/06/11/running-your-first-sph-simulation/