Title: A simple, quantitative method to infer the minimum atmospheric height of small exoplanets
Authors: Kipping, Spiegel, and Sasselov
First Author’s Institution: Harvard-Smithsonian Center for Astrophysics
Introduction

Figure 1. An artist’s illustration of the atmosphere of a gas giant exoplanet. Although it is possible to obtain spectra of the atmospheres of gas giants and some mini-Neptunes, determining the atmospheric properties of small planets is a major challenge today.
One of the major questions among astronomers who study planets around other stars is, “What kinds of atmospheres do exoplanets have?” This question is extremely challenging to answer empirically: not only are most exoplanets too faint and close to their stars for us to see directly (see this post for an exception), but their atmospheres (especially on small, potentially rocky planets) are only a tiny fraction of the planet’s total composition. In a few fortuitous cases, astronomers are able to measure properties of an exoplanet’s atmosphere by measuring either the spectrum of light that has passed through the planet’s atmosphere (transmission spectrum) or the spectrum that the atmosphere emits from its own thermal energy (emission spectrum). Figure 1 shows an illustration of a giant planet and starlight passing through its atmosphere. However, for Earth-size planets with small atmospheres, we do not yet have the instruments necessary to measure the tiny amount of light that passes through or emanates from their atmospheres.
Given our limited technical capabilities, what is the best way to learn about the atmospheres of exoplanets? The authors come up with a simple but clever method for calculating the portion of an exoplanet that must constitute an atmosphere. The premise of their model is that for sufficiently low-density planets, at least some part of the planet must be atmospheric. Although this idea is not new, the authors come up with a quantitative way of estimating the minimum height of the atmosphere for low-density planets.
The Method
To apply the authors’ method for determining a planet’s minimum atmospheric height, you need the following:
1. A measurement of the planet’s mass (this can be obtained through radial velocity measurements of the star or transit timing variations)
2. A measurement of the planet’s radius (this can be obtained through transit measurements)
3. A set of models describing how the mass and radius of a ball of a particular composition (for example, 75% water and 25% magnesium silicate) should relate. In this paper, the authors use models from Zeng & Sasselov.
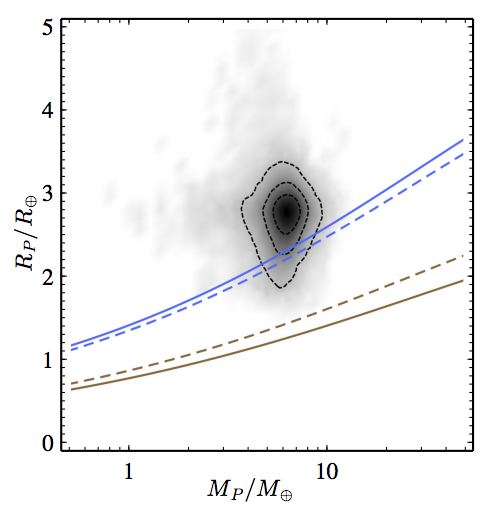
Figure 2. Planet radius versus mass. The black and gray blobs correspond to possible values of the mass and radius of the exoplanet GJ 1214 b from the mass-radius posterior probability density distribution; darker regions indicate higher concentrations of probable values. Black contours indicate the 1, 2, and 3 sigma boundaries on the distribution of possible masses and radii. The colored lines correspond to the mass-radius relations of various compositions: solid blue is 100% water, dashed blue is 75% water and 25% magnesium silicate, dashed brown is 25% magnesium silicate and 75% iron, and solid brown is 100% iron. Figure 2 in Kipping, Spiegel, and Sasselov.
The calculation is this: for a given mass and radius, calculate the difference between the radius of the planet and the radius corresponding to a planet of pure water (see Figure 2 for an illustration). This difference is the minimum height of the atmosphere.
Let’s examine how this works. If a planet’s solid and liquid portion (let’s call this the core) is 100% water, the radius of the core is that described by a constant water composition. Now, suppose the core of the planet is something denser than water, such as iron. Because iron is denser than water, the core will be smaller if it is iron than if it is water. Therefore, to make up the difference between the radius of the iron core and the observed planet radius, a planet with an iron core would need to have a larger atmosphere than a planet with a water core. Planet scientists generally agree that water is the lightest substance that could coalesce to form a planet core. Thus, by assuming a water composition for the planet core (and hence the maximum possible radius of the core), we can calculate the minimum possible height of the planet’s atmosphere.
Test Case: GJ 1214 b
The authors tested their method on the exoplanet GJ 1214 b. GJ 1214 b has been studied extensively. Its density is roughly consistent with a world composed entirely of water. Transmission spectroscopy of its atmosphere reveals a featureless spectrum consistent with either a water-vapor based atmosphere, or an atmosphere of lighter particles with a layer of haze.
Using recent measurements of GJ 1214 b’s mass and radius from Anglada-Escude et al. (2013, see Figure 2), Kipping et al. calculate the minimum atmospheric height for GJ 1214 b in these steps:
1. They draw a trial mass, radius combination from the posterior probability distribution (see Figure 2) of possible mass and radius values for GJ 1214 b.
2. They calculate the difference between the trial radius and the radius of a 75% water, 25% magnesium silicate planet of the same mass. This difference is the minimum atmospheric height. (Note: the authors prefer a 75% water, 25% magnesium silicate core, which is fairly consistent with planet formation theory, to the 100% water core, although either core composition could be used in principle. The authors also calculated the minimum atmospheric height with a 100% water core, which yielded consistent results.)
3. They iterate over all the mass and radius combinations in the posterior probability distribution. The collection of minimum atmospheric heights is the posterior probability distribution of the true minimum atmospheric height.
97% of the trials indicate an atmosphere on GJ 1214 b. The authors calculate a minimum atmospheric height for GJ 1214 b of 0.54 +/- 0.22 Earth radii, or an atmosphere that constitutes 20% of the total radius of GJ 1214 b. For comparison, Earth’s atmosphere constitutes about 0.1% of its radius. The authors argue that for GJ 1214 b’s atmosphere to be so extended, it should consist mostly of lightweight particles rather than heavy water molecules.
Conclusion
The concept of a minimum atmospheric height will be useful in trying to understand exoplanet atmospheres. Because the quantitative approach the authors take is simple and not too calculation-intensive, it could be applied to any exoplanet for which there is a mass and radius measurement. However, users should keep in mind that this is only useful for calculating a minimum atmospheric height. For dense, potentially rocky planets that lie below the 100% water line on the mass radius plot, this approach does not say anything about the presence or absence of an atmosphere. To learn more, we will need to improve our ability to measure atmospheres on such planets.
