Paper: The Global Schmidt Law in Star-Forming Galaxies
Author: Robert C. Kennicutt, Jr.
Institution: Steward Observatory, University of Arizona (now Institute of Astronomy, University of Cambridge, Cambridge, UK)
Stars form when cold gas in interstellar space collapses under its own weight. It is therefore not a stretch to think that the rate of star formation and amount of gas might be correlated. In today’s review of an “astrophysical classic,” we go back to 1998, and the seminal paper in which this correlation – now known as the “Kennicutt-Schmidt law” – is shown to hold across a wide sample of star-forming galaxies. This important relation not only hints at the underlying physics involved in the formation of stars, but is also a widely used prescription for modeling the star formation process in galaxy and cosmological simulations today.
A long time ago in a galaxy not so far, far away
The idea that the star formation rate (SFR) and gas density should be related started with a simple hypothesis stated in a key 1959 paper by Maarten Schmidt: “It is assumed that the rate of star formation…varies with a power n of the density of interstellar gas.” Schmidt supported his assertion with observational data of the solar neighborhood, concluding that the power law had an index of about two – a nonlinear relation. The ensuing decades brought better data and larger observational samples. After Schmidt, the attention gradually became focused on the global properties of galaxies rather than the nearby part of the Milky Way, as assembling a large sample of star-forming regions in our Galaxy is inhibited by source confusion and extinction thanks to our obscured vantage point within the disk. The x-axis of the relation – the gas density – originally was derived only from neutral hydrogen (H I) observations, as that was all that was possible in 1959; molecular line observations of CO (which traces molecular gas, a.k.a. H2) were first pioneered in 1970 by Wilson, Jefferson, & Penzias. Since stars directly form in molecular gas, this was a crucial step along the way. The Kennicutt-Schmidt law is typically formulated in units of surface densities – the star formation rate per unit area (ΣSFR) vs. the total gas surface density (ΣHI+H2). For galaxies, this removes the effects of a galaxy’s size or mass, rendering a comparison more meaningful.
Computing SFRs in galaxies
Estimating star formation rates is a tricky business. In nearby regions in the Milky Way, we can resolve individual stars, and thus simply look at young stellar clusters, count the stars, and then estimate their ages and masses. Not so in other galaxies – there one must rely on integrated, indirect measures. All the methods used to measure SFRs in this context leverage several important facts: (1) stars form in clusters; (2) massive stars dominate the luminosity of a cluster, particularly at short wavelengths; and, (3) massive stars have very short lives (see this applet). The procedure goes as follows. First, find a good tracer to observe. Some popular choices include ultraviolet emission (from the photospheres of massive stars), recombination radiation such as Hα (tracers of ionizing photons from massive stars), or infrared (dust-reprocessed ultraviolet) emission. Next, convert from luminosity in that tracer into a total number of massive stars. This step requires what’s known as “population synthesis” modeling, in which clusters (or even galaxies) of stars are simulated by combining models of stellar evolution, stellar atmospheres, and how stars are distributed in clusters as a function of their masses (the Initial Mass Function, or IMF). Observed luminosities in a tracer (say, Hα) are compared to model luminosities to infer how many massive stars are in the actual population. The IMF is then extrapolated to lower masses to estimate the total mass in stars. This mass is then divided by the timescale over which the model was evolved to determine a star formation rate for the cluster or galaxy.
Kennicutt’s data

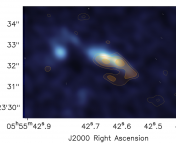
Figure 1: The spiral disk galaxy M51 (left) shows knots of star formation mostly concentrated in spiral arms. In contrast, the starburst Arp 220 (right) exhibits vigorous dust-enshrouded star formation throughout its center. Image credits: NASA/Hubble.
In this 1998 paper, Kennicutt aimed to comprehensively examine the correlation between the SFR and gas density across a large dynamic range of star-forming galaxies. His sample included 61 “normal” spiral galaxies as well as 36 additional galaxies in which a very active episode of star formation – a starburst – was occurring in their centers (see Figure 1). For the normal spirals (which are disk galaxies roughly similar to the Milky Way), he compiled Hα (to trace the SFR) and H I + CO (to trace the atomic + molecular gas) measurements of galaxies from the literature. For each galaxy, the total integrated measurements were converted to surface densities by dividing by the galaxy’s area (after correcting for the inclination). For the starbursts, he instead used infrared data to calculate SFRs, as these engines of star formation are teeming with visible/ultraviolet-absorbing dust. Since the dust absorbs almost all the energy emitted by the starburst and then radiates it at its own blackbody temperature (or more accurately, temperatures, as there are likely multiple dust populations within a galaxy), the total infrared luminosity becomes a very reasonable tracer of the SFR in these systems. As the gas in starbursts is predominately molecular, Kennicutt used only CO (and not H I) measurements to estimate their gas densities. He converted integrated measurements to surface densities by dividing by the size of the starburst region, which is typically about a square kiloparsec.
A strong correlation with lots of scatter
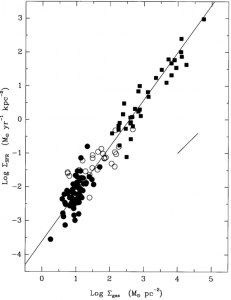
Figure 2: The original Kennicutt-Schmidt diagram, which plots the surface density of star formation against the gas surface density. The relation is shown for normal spiral galaxies (filled circles) and starburst nuclei (squares). The open circles are the central regions of selected disk galaxies. Kennicutt found a power law correlation with slope 1.4 that holds across many orders of magnitude.
Plotting the results for all 61 spirals alongside the 36 starbursts, Kennicutt showed that a superlinear (slope N≈1.4) power law is an excellent empirical description of the relation between the star formation rate and gas surface densities across more than six orders of magnitude in SFR in galaxies. Figure 2 shows the original “Kennicutt-Schmidt” diagram that is now almost ubiquitously seen in talks about star formation in galaxies, either observational or theoretical. Let’s deconstruct this plot just a bit more.
First, while the correlation is quite remarkable, there is still significant scatter present. Amongst the disk galaxies (the black circles), up to a factor of 30 difference in SFR is seen at a fixed gas density. Part of this may be due to how Kennicutt corrected for extinction in his Hα data: lacking any more robust means to determine how much of the Hα emission in the galaxy was being absorbed by dust, he simply assumed an extinction of 1.1 magnitude (a factor of 2.8 change in flux) for all galaxies. There is also some variation in how well CO traces H2 (the infamous “X-factor”) as a function of the physical conditions of the gas. While the actual amount of extinction and the value of the X-factor most certainly vary between (and within) galaxies, it is still unlikely that differences in these two factors alone could explain the full factor of 30 difference in SFRs across the sample. This suggests that much of the scatter actually represents real variations in the star formation efficiency (how long it takes the gas to turn into stars globally).
Second, the correlation for the spirals alone is much less robust than the combined correlation. It is the addition of the starbursts that provides the lever arm to achieve the high dynamic range that makes the correlation robust. (To see this, place your hand over the right half of the plot and try to draw a line through the remaining points).
Third, since the relation is superlinear, the efficiency of star formation – the SFR divided by gas density – seems to increase with increasing gas density. What does this mean? Kennicutt offers a theoretical argument for why this might be the case. If self-gravity in a gaseous spiral disk controls the formation of stars, the SFR volume density should scale as the gas volume density ρgas divided by the timescale for the growth of gravitational perturbations in the disk. Since the latter goes as the free-fall time tff~(Gρgas)-1/2 this suggests that the SFR should scale as the gas density to the 1.5 power – very similar to the value of 1.4 observed. To convert between volume and surface densities, a constant disk scale height must also be assumed. This is however not the physical basis for the Kennicutt-Schmidt law, but simply a plausibility argument.
Recent progress
Kennicutt’s seminal 1998 paper combined with rapidly improving observational facilities in the early 2000’s led to a burgeoning in this field. Increased resolution has now allowed resolved studies within galaxies, and the ΣSFR-Σgas relation appears to hold at kpc scales within disk galaxies, as well as amongst entire disk galaxies. Interestingly, the majority of work at these kpc scales finds a linear relation — N ≈ 1 – instead of the superlinear relation Kennicutt originally derived. Furthermore, the role of the molecular gas has now been isolated: the correlation between the SFR and H2 is much tighter than that between the SFR and HI+H2. Additionally, modern studies typically use multiple star formation tracers, e.g. Hα (to trace recombination radiation that escapes the galaxy) plus mid-infrared (to trace the portion absorbed by dust). For interested readers, Kennicutt & Evans (2012) provide a detailed and comprehensive (though dense) review of this subject in a review paper, which I highly recommend.
There has been incredible progress over the last two decades in understanding the fundamental process of star formation. However, it is important to remember that the Kennicutt-Schmidt law is an empirical one. It is widely cited, widely studied, and widely used as a prescription in simulations. But the physical basis for a power law relation between the star formation rate and gas density has not yet been clearly determined. And that is why, as they say, this is still a very relevant topic of active research today.
“Astrophysical classics” is a series of articles that delves into seminal papers from the astronomical past and places them in the context of modern research.




Trackbacks/Pingbacks