- Title: Long Time–Scale Behavior of the Blazhko Effect From Rectified Kepler Data
- Authors: J. M. Benkő et al.
- First Author’s Institution: Geneva Konkoly Observatory
- Paper Status: Accepted to The Astrophysical Journal
Chaos theory is a field of mathematics that studies systems whose long–term behavior is greatly dependent on initial conditions. On Earth, the chaotic nature of weather leads to the famous “butterfly effect”, in which the flapping of a butterfly’s wings can theoretically create a hurricane. Chaos is a fundamental element of nature which can arise in many environments—including stars.
A Trip Into Chaos
Let’s take a step back: If you’re unfamiliar with chaos, you may confuse it for “randomness”. However, chaotic systems are completely deterministic. The key feature of chaos is that a slight shift in initial conditions of your system can completely change its trajectory. One example you may have seen in your classical mechanics class is the double pendulum. This is a great simulation that can help you visualize chaos. If you slightly alter the starting position of the pendulum, you can see that its path dramatically changes. Despite what appears to be impossibly complex behavior, it is easily explained with simple physics!
Now back to astronomy and the topic of today’s paper: RR Lyrae stars oscillate in brightness twice a day. However, they are not strictly periodic because the amplitudes of the oscillation vary with time. These variations are often periodic themselves but with a much longer time scale. A great animation of this effect is shown here. This phenomenon was first seen by astronomer Sergey Blazhko in 1907. It has since been named the Blazhko effect, and the period of the peak amplitude variations is known as the Blazhko period. This effect is thought to arise from exciting asteroseismic modes in the RR Lyrae stars, and these excitations may lead to chaos. However, hunting for chaos requires dedicated and systematic observations. Because of this, our understanding of the Blazhko effect has been limited until very recently.
The Kepler Revolution
Today’s paper looks at this phenomenon with a telescope that is normally associated with exoplanets—Kepler. In order to fully understand the chaotic nature of RR Lyrae stars, the authors needed a long, continuous data set and an aperture capable of capturing the full light curve of the stars in question. Kepler is great at the former, but it is designed to search for small dips of light to detect exoplanets. Because of this, the “optimal” apertures used to detect exoplanets cut out a small fraction of the host star’s light. Removing RR Lyrae light, however, would lead to an inaccurate light curve. To complete this study, the authors created larger, specialized aperture masks to capture the full light curve of the RR Lyrae stars.
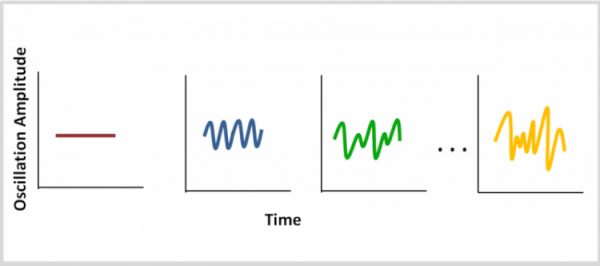
Figure 1: Period doubling leads to chaotic behavior. Here the oscillation peaks vary between one value (red), two values (blue), four values (green) and many values (yellow). The doubling of equilibrium values corresponds to a doubled period. This doubling will eventually lead to chaotic behavior with an “infinite” period i.e. a non-repeating signal. The colors correspond to the regimes shown in Figure 2.
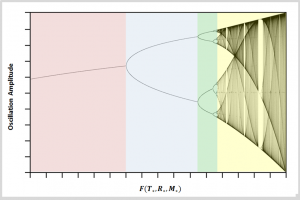
Figure 2: Period doubling leads to chaos. The oscillation amplitudes can change with the star’s parameters (like temperature, radius or mass). The colors correspond to the light curves shown in Figure 1. This period doubling cascades into chaos as the amplitude bounces between many different oscillations amplitudes (yellow area). [Original Image from Wikipedia Commons]
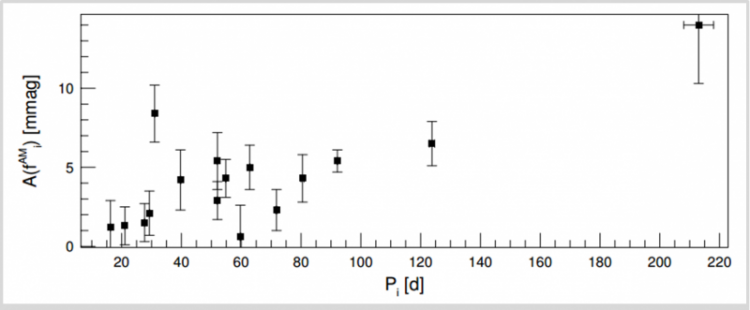
In addition to the RR Lyrae stars which exhibited period doubling, the team found one star which appears chaotic and two more stars on the verge of chaos. What’s more, the authors find that many of these detected frequencies can be traced back to the star’s radial vibrations and that the amplitudes of the vibrations increase with the Blazhko period (shown in Figure 3). This new observational evidence suggests that resonances of radial vibrations may lead to the chaotic instability seen within the star. Hydrodynamic models are being developed to fully understand this phenomenon, but we are now much closer to solving this century–old mystery.
Figure 3: Average amplitude of the modulation vs the Blazhko period. The amplitude of the modulation appears to be correlated with its period. (Fig. 9 of Benko et al. 2014).
Trackbacks/Pingbacks