- Astrobites Classics: Aerodynamics of solid bodies in the solar nebula
How do planets form? - Author: S. J. Weidenschilling
- Affiliation: AA(Carnegie Institution of Washington, Washington, D.C.)
- Year of publication: 1977
Fundamental for planet formation: Dust dynamics
Planets have been observed all over the Milky Way. Though more and more exoplanets have been and will be detected, it is still uncertain how planets generally form. Although there is a huge variety of suggested models, they all have one thing in common: They all consider dust dynamics in the protoplanetary disk. In today’s Astrobite, we will explore one of the classical works in the field of planetary formation by Stuart J. Weidenschilling.
The underlying assumption of the study is that planets form via growth of orbiting dust particles in the protoplanetary disk. The author investigates the dynamics of dust particles of different diameters in a gaseous disk. First of all, consider a constant dust particle size. The more gas there is in the disk, the higher the gas viscosity and drag force felt by the dust particles. Physicists often distinguish between two regimes: When the dust particle is larger than the mean distance between gas particles (also known as the mean free path), it is in the so-called Epstein regime; On the other hand, when the dust particle is smaller than the mean free path of the gas particles, it is in the Stokes regime. Weidenschilling considers both regimes and furthermore separates the Stokes regime into three sub-regimes depending on the strength of viscosity. Based on this, he derives equations for the radial velocity of the particles initially surrounding the Sun in circular orbits.
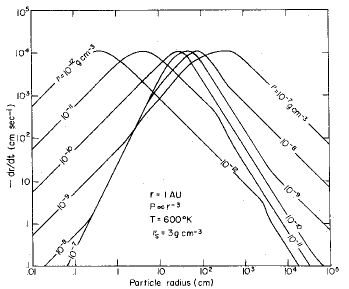
Figure 2: Radial velocity distribution for particles of different radii at 1 AU illustrating the shift of the peak to larger radii for increasing gas density.
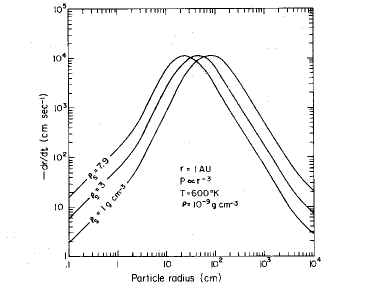
Figure 1: Radial velocity distribution for particles of different radii at 1 AU illustrating the shift of the peak to lower radii for increasing dust density.
Meter-size barrier
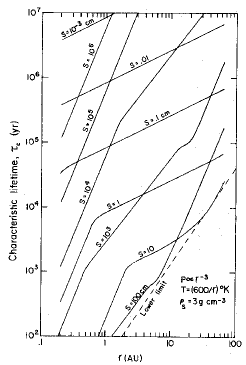
Figure 3: Lifetimes for particles of different sizes depending on their radial distance from the Sun.
Weidenschilling finds a very interesting result. The maximum radial speed (also called drift speed) is independent of the assumed gas mass in the protoplanetary disk. With respect to this, the maximum speed of the particle is the same regardless whether it is in the Epstein or Stokes regime. However, the author finds a strong correlation between dust particle size and radial speed as seen in figure 1 and figure 2 of this Astrobite (figure 3 and figure 4 in the original paper). On the one hand, very small particles have low drift speeds because they basically follow the mean motion of the gas. On the other hand, if the objects are big enough the gas cannot disturb their orbits efficiently and they only drift towards the central star very slowly, too. Thus, there is a maximum drift speed for particles in between the two extremes. Increasing the dust density causes a shift of the peak to smaller particle sizes, while increasing the gas density shifts the peak to higher values. However, the shape of the function of drift speed versus dust particle size remains roughly the same on the logarithmic scale for most probable gas and dust densities, Weidenschilling finds an important result: Among all particles, meter size particles have highest drift speeds of about 100 m/s.
The author expands the study to further calculate the drift speeds for different orbital distances. From the derived velocity distribution, he finally calculates typical lifetimes for particles of different radii, which are shown in Figure 3 (Figure 6 in the original paper). The fact that drift speeds are highest for meter-size bodies marks a crucial limit for planet formation; the so called meter-size barrier. Particles of meter-size at orbits smaller than 7 AU fall into the Sun already after less than 1000 years. That means that planets have to grow from meter-size bodies either extremely quickly at small orbits or they have to grow at orbits further outside, and migrate inwards at later times. However, such high speeds of up to 100 m/s make it generally very challenging to grow to larger than meter sized objects since colliding speeds of this order will rather destroy the bodies via fragmentation or erosion.
Now, if you hear anybody talking about the meter-size barrier, you know what’s going on. Obviously, the model is simplified in many sense, as for instance; it assumes constant particle sizes and ignores the growth of particles, disk asymmetries, internal disk turbulence and assumes simplified power laws for temperature and pressure. Nevertheless, even 38 years after publication of the study, there is still no commonly accepted solution to circumvent the barrier – though there are many different suggestions. Stay tuned if you are interested in planet formation since you can read more about possible solutions to circumvent the problem in future Astrobites.



Have there been any more recent simulation studies looking at this problem?
It is a hot topic of research and many groups investigate it in models of protoplanetary disks and planet formation.
Can these planetesimal particles collect gases as the zip by? This way the “collision” isn’t likely to destroy the planetesimal while it still grows in size.
Good point. You suggest that the gas can act like a buffer, right? The fact that the gas might be part of the growth is neglected in this study. However, you need to form larger bodies before the gas can accrete around it. In that sense the meter-size barrier remains.
I’m confused by Figure 1 – why would the velocity be lower for 0.1 – 1 cm sized particles, go up, then go back down for 10^3 – 10^4 cm sized particles? It seems like the velocity would just decrease with particle size as they get more massive.
Maybe the meter-sized gap is why Rosetta observes Churyumov-Gerasimenko as composed by granules? Even the meter sized “rocks” are such, was my impression from the press releases and images.
Another win for Rosetta in that case, constraining the (outer) disk accretion process.
@Zoey: “… why would the velocity be lower for 0.1 – 1 cm sized particles, go up, then go back down … ?”
It seems to this layman reader the key part in the text description is this:
“On the one hand, very small particles have low drift speeds because they basically follow the mean motion of the gas. On the other hand, if the objects are big enough the gas cannot disturb their orbits efficiently and they only drift towards the central star very slowly, too. Thus, there is a maximum drift speed for particles in between the two extremes.”
Yes, you’re absolutely right.
This is a very thorough description of the meter-size barrier problem. Seems like something that further computer simulations will have to resolve eventually.
Thanks for this post! Even though there’s no consensus on how to resolve the meter-size problem, are there any theories that you find particularly interesting or persuasive?
Is it possible that perturbations in the density of particles in the disk could solve this problem? With an over-density of meter-sized bodies in one area, would they form larger bodies quickly enough to overcome the problem?
Have we been able to observe or find any protoplanetary disks?
Yes, and plenty more will be observed by ALMA. You might have seen the image of HL Tau in the news.
http://en.wikipedia.org/wiki/HL_Tauri
Very nice post of a still much debated Astro topic!
Thanks for the really cool post and explanation. It’s really nice how these simple theoretical calculations end up becoming the most influential. The analytic results mentioned here have generated so much more interest than their more accurate, detailed simulation counterparts!