Title: Simulations of protostellar collapse using multigroup radiation hydrodynamics – The first collapse and The second collapse
Authors: N. Vaytet, G. Chabrier, E. Audit, B. Commerçon, J. Masson, J. Ferguson, F. Delahave
First author’s affiliation: AA (École Normale Supérieure de Lyon)
Date of publication: 2012 and 2013
Paper status: published in A&A
Drama scene
Set: Party
Characters: Astronomer, other guest not affiliated to astronomy
The astronomer and the other person meet, feel attracted to each other and at the end of the party, they decide to leave the party together.
Guest (making eyes at the astronomer): “Let’s sit down for awhile and you can tell me more about the stars!”
Astronomer (with shining eyes): “Well, do you know how star formation works?”
Guest (slightly surprised): “… No, I don’t. Tell me.” (ogling even stronger now)
Astronomer (enthusiastic): “It’s really fascinating and not so difficult too understand! A star forms mainly due to gravitational collapse, well, there is more to that, but as an assumption, you can ….”
Other person (thinking): “This is hopeless. I’ll sleep alone tonight.”
If you recognize yourself as the astronomer in the above scene, then you’re lucky; today’s bite deals with the details of the collapsing phase of star formation, especially the formation of the first and second core.
Phases of star formation described by open, closed and broken doors
As an analogy, imagine the collapsing phase to a protostar as the following sequence: closing a door first and then breaking it down. You’ll understand what I mean in the following. As the astronomer in the scene above said, stars form due to gravitational collapse of dense cores. While the gas inside the core collapses, the density at the center increases. Eventually, the density becomes so dense that it becomes optically thick to its own radiation. What does that mean? It means that the energy, which is produced in the collapse cannot be radiated away from the inner region any more and will be absorbed by the surrounding gas instead; the door is closed for radiation to leave the core. Astrophysicists say that this is when the first core has formed. Since the energy cannot escape the collapsing gas any more, the first core starts to heat up and counteracts the gravitational contraction. The phase ends, when the molecular hydrogen (H2) starts to break apart (dissociate) at a temperature of about 2000 K. The break up of molecular hydrogen reduces the increase in temperature significantly and the core undergoes a second (nearly) isothermal collapse phase. Loosely speaking: The door for collapse is broken down until all molecular hydrogen is burnt. After the dissociation phase, the second collapse is over and the second core has formed. Hereafter, a new door has been installed and the core contracts slowly again since the heating up counteracts gravity (see figure 1).
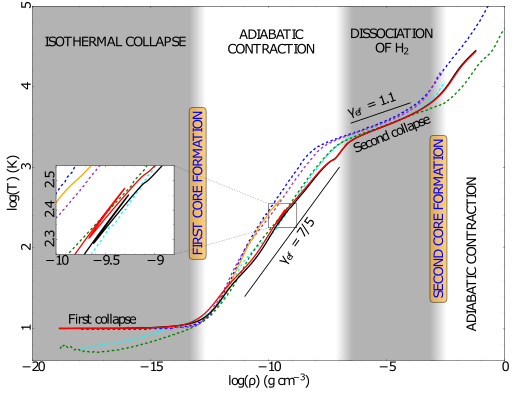
Fig. 1: The figure illustrates the evolution of star formation from first collapse until the the formation of the second core. The different lines show results from different models. The dashed lines are from previous models, while the solid lines illustrate the authors’ results. The solid red line shows the curve for their multi-frequency approach and the solid black line a frequency independent – so called grey – approach. As you can see, the results do not differ significantly for the frequency dependency. (The figure is Fig. 6 in the original paper dealing with the second core.)
Results of the paper: Frequency dependence is unimportant and second core properties are independent of initial conditions
The entire process includes a lot of physics and the authors focus on how the energy induced by the compression of the gas is transported during collapse of the dense core. In astrophysical terms this form of transport is called radiative transfer. What is different in the authors work compared to previous studies is that they take into account the fact that the radiation of energy is different for different frequencies. In previous studies the emissivity of the gas was assumed to be the same for all frequencies, called grey assumption. Nevertheless, the authors want to avoid to use too much of their limited computing resources and thus approximate the frequency dependence by summarizing frequencies within a range to get a couple of frequency bins. You wonder what “bin” means? Consider the following: as opposed to have numbers 1,2,3,4,5…99, 100 we would lump together 1-50 and 50-100. We’ve cut down the number of calculations from 100 to 2. That’s what the authors do. However, the authors find that there actually is no significant difference by taking into account the dependency on frequencies and a simple grey approach. As a remark for the evolution after the second core, the authors point out that they expect a frequency dependence for appropriate modelling. Vaytet et al. consider the collapse of a 0.1, 1 and 10 Msun cloud and they find that first cores have typical sizes of about 10 AU, lifetimes of a bit more than 1000 years and contain about 2% of a solar mass with slightly larger numbers for increased initial mass. The conditions of the second core turns out to be completely independent of the initial conditions and the authors estimate typical masses of about 10-3 Msun and 3*10-3 AU in radius.
Conclusion
Two results are interesting here: First, their results suggest that modellers can get away with ignoring the frequency dependence to save computational time. Second, the second core properties seem to be independent on initial core conditions. This would mean that similar stars might evolve from very different initial conditions. (Just as it happens in real life: Obama and Bush have a very different background and yet, they both became president.) Thus, it might be that the differences in stellar mass and size actually stem from processes after the second core collapse. A question, which probably can be answered not too far in the future by using more sophisticated three dimensional simulations (and extra computational time).