Title: Lens Masses and Distances from Microlens Parallax and Flux
Author: J. C. Yee
First Author’s Institution: Harvard-Smithsonian Center for Astrophysics, Cambridge, MA
Status: Submitted to The Astrophysical Journal Letters

When stars were divine, and their journeys across the heavens foretold the events to unfold on our humble terrestrial sphere, the alignments of stars were studiously marked.  They signaled the rise of new dynasties, a lucky windfall, ill-fated love.  With the passage of a few millennia (and the realization that the wandering stars were planets), our modern sensibilities have been honed to instinctually interpret the apparent crossing of stellar paths as just a happy but natural coincidence with no deeper significance.  But perhaps mistakenly so.  For when the stars align, you just might catch a glimpse of things otherwise invisible:  binary stars in wide orbits, isolated black hole hermits, or the abandoned (or unruly) free-floating planet far from the star around which it was born.

These invisible wanderers are quite literally brought to light through a unique sequence of events that occurs when two celestial bodies align.  The force that orchestrates the event?  Gravity.  Black holes have gotten much fame for their gravitational brawn, which grants them the abilities to warp space and time and to bend light.  Such powers, however, are actually not limited to black holes alone—they’re bequested on anything with mass.  Your everyday celestial body—say, a star or planet—can do precisely the same.  The share of the limelight that black holes have been given in this regard is fairly earned, however, as the ease with which you can see the distortions caused by a massive object scales with its mass.  Such objects can act as a lens by virtue of their spheroidal shapes, focusing the stray light beams passing from behind into a distorted image.  This process is known as gravitational lensing.

For objects as small as stars, you can’t see these images.  The images would be tiny—about a million times smaller than the angular diameter of the Moon—hence the name of this class of gravitational lensing events, microlensing.  But these minuscule images can have a disproportionately large detectable effect.  When a star crosses paths with another, you’d observe the background star to brighten drastically—as much as a factor of a 1000!—then dim.  The two stars don’t have to pass directly in front of each other, but the closer they do, the more the light from the star behind (the “source” star) will be focused. Maximal brightening occurs when the source and the lens are at exactly the same position, a special point called the caustic. Over weeks to months, a distant observer would note a single brightening, then dimming of the star.  If the lensed star had any companions—a fairly likely scenario, as stars often come in pairs, and most (if not all!) are believed to have planets—its caustic can morph from a point into a series of closed curves (see Figure 1). If the source star approached or crossed these curves, we’d observe additional brief spikes in light. Depending on how the mass of the companion compares to the lensed star, these spikes can be as short as a day (for low mass companions such as planets)—a real challenge for planet hunters searching for microlensed systems.

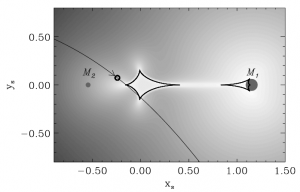
Figure 1. The geometry of a a microlensing event.  The path of the background star (the “source” of light) is shown by thin gray curve; the arrow shows the direction it moved along this line.  The foreground lensing object is a binary system, likely a brown dwarf (M1) with a planet (M2).  The background is shaded in different shades of gray to show how much the binary could cause the background star to brighten (see Figure 2 for what was observed).  The dark black curves denote the “caustics” of the binary lens: when the background star crosses a caustic, it momentarily becomes infinitely bright if the background star was a point (which is unrealistic—we know stars have finite sizes!).  Figure from Han et al. 2013.

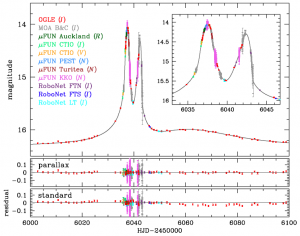
Figure 2. A microlensing lightcurve. The lightcurve (brightness over time, here in days) observed for the system shown in Figure 1. The two peaks occur when the background star crosses the caustic (which, as you can see from Figure 1, occurs twice). Figure from Han et al. 2013.

Microlensing events, however, lack one piece of information prized by astronomers—masses.  The lens mass affects how long a microlensing event lasts.  The duration of a microlensing event is easy to measure, but it also depends on three other things: how far away the lens is, how far the source is, and how fast they’re moving relative to each other.  Thus in order to derive the mass of the lens, we need to determine the other three.  The distance of the source is easy—typical sources are in the Galactic bulge, the concentration of stars at the center of our galaxy, which is a well known distance away (about 8 kpc).

The author of today’s paper suggest a two-step process to determine the remaining three unknowns.  The first is to make two microlensing observations of the same event, but at different places (and thus different angles).  Such a “microlens parallax” measurement—which has just recently become possible to obtain for many microlens events due to a new campaign to search for space-based microlensing events with the Spitzer Space Telescope—allows you to reduce the unknowns to the lens mass and distance.  This leaves you with the classic problem of having a single equation with two unknowns, for which there are an infinity of permitted combinations.

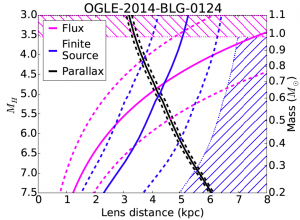
Figure 3. Disentangling the mass of the lensing star.  If you can observe a microlensing event from two different angles, you can derive a mass/magnitude-distance relation (black; the dashed line denotes the uncertainty).  Measuring the flux from the lensing star also produces a magnitude-distance relation (magenta).  The place where the two lines cross gives the mass and distance of the lens.  In the special case in which you have a binary lens, the size of the source star affects how bright it gets, which allows you to derive another mass-distance relation.  Figure from today’s paper.

The final key to the puzzle?  The flux from the lens, if it’s bright enough.  If the lens is a star, its flux allows us to measure how far away it is, given that we know how luminous it is.  Since we don’t often know how luminous a given object is, this yields a magnitude-distance relationship.  Based on our understanding of stars, the mass-distance relationship obtained from a microlens parallax measurement can be converted into a second (and very different!) magnitude-distance relationship (see Figure 3).  Whatever magnitude-distance combination that’s permissible by both relationships gives you the distance to the lens—which finally allows you to solve for the mass of the lens.

And there you have it.  It may seem like a long and difficult process to obtain the mass of a fleetingly visible object, but these mass measurements will help us to understand planets and stars of our galaxy that are currently unreachable by another means.  With additional Spitzer microlensing campaigns—the first of which is already returning a treasure trove of results—as well as the revamped Kepler mission, K2, and the upcoming mission WFIRST, space-based microlening surveys may become routine.  It’s an exciting time for microlensing—many new discoveries await!

Cover image:  A map of the amount of brightening you’d see if a distant star passed behind one of the stars in a equal-mass wide binary.  The black curves denote the lens’s caustic—if the background star crossed this curve, would momentarily become infinitely bright if it was a point source.   The path of the distant background (source) star would appear as a line across the image.  You can predict the lightcurve of the microlensing event by plotting the brightening along the source star’s path.  Figure from Han & Gaudi 2008.

• About the Author

About Stacy Kim

I was a former graduate student in The Ohio State University's Department of Astronomy. On a day-to-day basis, you could typically have found me attempting to smash clusters of galaxies together inside big supercomputers to see if cluster mergers are good testbeds for dark matter collisionality. As an undergraduate at Caltech, I spent a few years chasing photons where planets are thought to form (or, as they say, performing Monte Carlo radiative transfer calculations of protoplanetary disks) at NASA's Jet Propulsion Laboratory. When I wasn't sitting in front of a computer trying to translate cosmic thoughts into pithy lines of code, you could often find me in the kitchen or on the walls of a climbing gym.

Related posts:

A super-precise super-Earth: measuring a planet’s radius to within 120 km A Crippled Kepler Discovers a New Planet WASP-47b: A Hot Jupiter with Friends 6 Real Planets That Put Science Fiction (And Cracked) To Shame