Guide to Empirical Velocity Laws

by | Jun 30, 2016 | Daily Paper Summaries, Guides | 0 comments

Key words: Faber-Jackson relation, Tully-Fisher relation, M \propto \sigma relation, stellar velocities, empirical relations

Lost in the forest of articles

If you read this line chances are pretty high that you are interested in astrophysics. In case you are an astronomy student you might know this dilemma: You want to learn about astrophysics and dive into the literature, but you have no clue where to start and what articles are important to read. There are just so many articles published every day that there is obviously no chance to read all of them. What can you do about it? First of all: relax. You are already on the right track by reading the paper summaries on astrobites.org to get an idea of what is currently going on in research. However, judging the impact and importance of a paper usually requires some time. Generally, the impact of articles decays over time because the raised issues were either falsified or considered as being irrelevant. Only a tiny fraction of publications defy this trend and remain as milestones in the field. These are the classical articles, or more precisely the important results in them, you want to be aware of.

The magic key: Stellar velocities

Looking at important papers during the last ~50 years, the four milestones presented in this astrobite provide a striking similarity. Besides the large number of citations (all having more than 1000 citations), they have in common that all four present a relation based on the same physical quantity: velocity. The four papers present a relation between the velocity of stars at the center of galaxies and the luminosity of the host galaxies (Faber & Jackson, Tully & Fisher) or the mass of the supermassive black hole at the galaxy’s center (Ferrarese & Merritt, Gebhart et al.). While the Faber-Jackson relation applies to elliptical galaxies, the Tully-Fisher relation applies to spiral galaxies and the M \propto \sigma (Ferrarese & Merritt and Gebhart et al.) relation to the galactic bulges. Let’s have a look what makes the three relations so important.

Faber-Jackson relation

Faber and Jackson measured velocities of stars at the center of elliptical galaxies. Based on these results they calculated how much the velocity of each star differs from the average velocity of all the stars at the galactic center. The average of the differences yields the so called velocity dispersion and is a measure of the scatter. Faber & Jackson found that the luminosity of elliptical galaxies scales with the velocity dispersion of central stars in elliptical galaxies as L \propto \sigma^{\gamma} , where \gamma often is about 4 (see Figure 1).

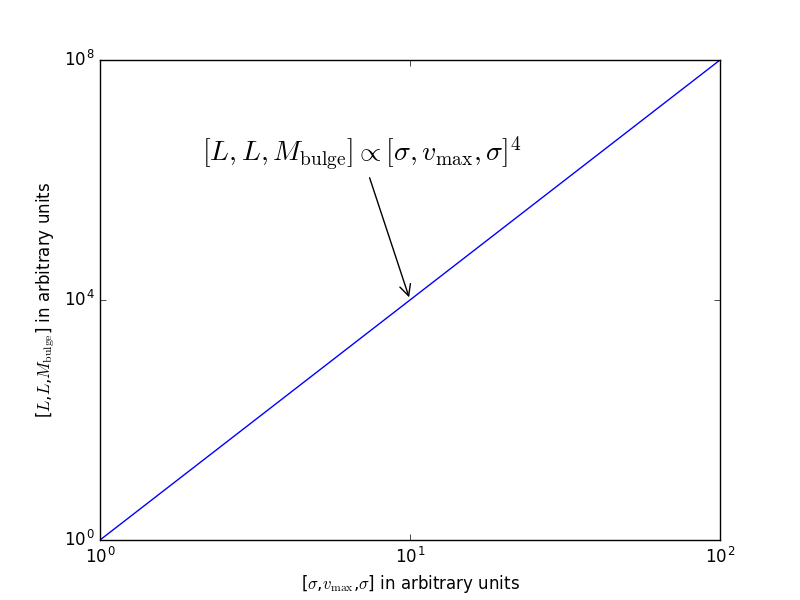
The Faber-Jackson, Tully-Fisher and $latex M \propto \sigma$ relation all show the same dependency of $latex y \propto x^4$. In the case of Faber-Jackson, the y variable is luminosity of the center of an elliptical galaxy and x is the stellar velocity dispersion, for the Tully-Fisher relation y is the luminosity of the center of a spiral galaxy and x is the maximum rotational velocity of the stars at the center and for the $latex M \propto \sigma$ relation it y is the mass of the super massive black hole and x is the stellar velocity dispersion at the center of the bulge.

The Faber-Jackson, Tully-Fisher and M \propto \sigma relation all show the same dependency of y \propto x^4. In the case of Faber-Jackson, the y variable is luminosity of the center of an elliptical galaxy and x is the stellar velocity dispersion, for the Tully-Fisher relation y is the luminosity of the center of a spiral galaxy and x is the maximum rotational velocity of the stars at the center and for the M \propto \sigma relation it y is the mass of the supermassive black hole and x is the stellar velocity dispersion at the center of the bulge.

Tully-Fisher relation

Similar to the work by Faber & Jackson, Tully & Fisher found that the luminosity of spiral galaxies scales with the maximum of the rotational velocity of the stars at the galactic center as L \propto v_{\rm max}^{4}. You can see that in both relations the luminosity scales with a velocity dependent quantity to the fourth power. This is not a coincidence, but rather the consequence of an approximately constant ratio of stellar mass to stellar light and the fact that the galactic center shines uniformly as can be seen in this brief theoretical explanation. (To remember which relation has to be used for what type of galaxy use this alphabetical crib: DEF: Dispersion in Elliptical galaxies yields Faber-Jackson, RST: Rotational velocity in Spiral galaxies yields Tully-Fisher)

M \propto \sigma relation

A more recent discovery is the M \propto \sigma relation, which was revealed in the two remaining papers in 2000. The two groups measured the velocity dispersion of stars around a supermassive black hole and compared it to the mass of the supermassive black hole. In the same line as Faber & Jackson, they find a scaling of the velocity dispersion to the fourth power. No surprise that people refer to the result also as the “Faber-Jackson relation for black holes”.

Measuring the luminosity of galaxies or the mass of supermassive black holes are observationally difficult tasks. However measuring stellar velocities is much easier and thanks to the relations you can retrieve information about the luminosity or supermassive black holes from velocity measurements. If it is the luminosity you determined, you know the amount of light produced by the galaxy. The galaxy emits in all directions and the farther you are from the light source the darker it appears. Therefore you can compare the computed luminosity with how bright the galaxy appears when observing it on Earth (apparent magnitude) and voilà: You estimated how far the galaxy is away from you!

The importance of the relation

It is especially the possibility to estimate distances of galaxies based on the Faber-Jackson and the Tully-Fisher relations that make these relations useful. The M \propto \sigma relation instead might suggest that every galaxy contains a supermassive black hole, but the debate is still ongoing. Finally, be careful! The relation might be less general than presumably assumed and can be biased (for a critical discussion, please read this astrobite). Nevertheless, the relations are important and get frequently cited. Isn’t it great that you now know what they are about? Don’t fear them anymore when you stumble over them on your way through the forest of astrophysical articles.

About Michael Küffmeier

I'm in the first year of my three-years PhD at the Niels Bohr Institute under the supervision of Åke Nordlund in Copenhagen. Besides fighting Scandinavia's bipolar disorder of darkness in winter time and overwhelming brightness in summer, I'm currently working on zoom-simulations. More precisely, on magnetohydrodynamic simulations of star and protoplanetary disk formation carried out with an adaptive-mesh refinement code called RAMSES. When I'm not in the office or traveling I'm probably somewhere else. If the weather allows it, I'm on the beach to improve my poor kite-surfing skills - with rather modest success.

Related posts:

Astrobites: A Look back at 2016! Two (or three?) black holes in one galactic center Gravitational Lensing in the Canary Islands Biases in Astronomy: Is the M-sigma relation an upper limit?

Leave a Reply