A Pebbly Barrier to Planet Formation

Title: How much does turbulence change the pebble isolation mass for planet formation?

Authors: S. Ataiee, C. Baruteau, Y. Alibert, W. Benz

First Author’s Institution: University of Bern, Physics Institute, Space Research and Planetary Sciences

Status: Accepted for publication in Astronomy and Astrophysics, open access on arXiv.

Introduction

Building a planet is a messy process, and astronomers are still unsure of how certain steps work. Planets are born from the same nebula that forms the star they orbit. As the nebula collapses, it flattens out, due to the gas’s angular momentum. This becomes the star’s protoplanetary disk, where the planets are born. Within this disk, small instabilities can lead to the growth of planetesimals. Some of these will continue to gain mass and will eventually become planets. How exactly they gain mass, though, is still up to debate.

The two most popular models are core accretion and disk instability. In the core accretion model, planetesimals in the protoplanetary disk collide and stick together. Eventually the core will become large enough that it begins to accrete more and more material onto itself. In the disk instability model the disk becomes unstable when it becomes massive enough. This leads to small regions undergoing local collapses, forming planets.

Combinations of the two theories have been proposed, but details are still being worked out. One large problem is that the time scale for disk instability is very short while core accretion takes a long time. There are also questions about whether or not planets remain at the distance where they formed. Discoveries like hot Jupiters raise questions about whether planets might migrate inwards or outwards from the star.

Today’s paper takes a closer look at one of the remaining problems of planetary formation – how a planet’s mass can prevent it from accreting more material.

Trapping Pebbles

During a planet’s formation, grains in the millimeter to centimeter size range form an important source of mass. As the planet is forming, these pebbles can accrete onto the planet quite efficiently, since they experience a drag force from the surrounding gas. This reduces their velocity relative to the planet, allowing them to fall onto its surface. However, as the planet grows in mass, it opens a gap in the gas disk. This gap is created by the transfer of angular momentum to the gas by the planet’s wake. Because of this, the gas’s orbital velocity will increase, causing it to move outwards. The outward flow of the gas will create a pressure bump. This pressure will prevent pebbles from falling inwards towards the planet anymore. They will be trapped in a ring at the outer edge of the gap the planet has opened.

Figure 1: This image shows how a planet creates a barrier preventing pebbles from coming closer. Once the planet has started to clear its local orbit, the shock of its wake will force gas outwards, creating a radial pressure. This pressure prevents pebbles from falling inwards. Image taken from Chatterjee & Tan (2013, arXiv:1306.0576)

The mass at which pebbles become confined to this ring is known as the pebble isolation mass (PIM). Once a planet reaches this mass, the continued accretion of pebbles is very inefficient. This represents a very important step, because the planet must use some other method to accrete mass after this.

The Role of Turbulence

In today’s paper, Ataiee et al. analyze what effect the turbulence of the disk has on the PIM. They did so by assuming that the PIM relies on several properties of the gas in the disk. The primary parameter was the ratio between the disk’s height and the distance from the star, as (called the aspect ratio). They also used the gas’s turbulent viscosity , which is the viscosity of the fluid caused by internal fluid friction.

Using the code Dusty FARGO-ADSG, they ran hydrodynamical simulations on disks of gas and dust. FARGO is a program designed to solve the equations of hydrodynamics, optimized for disks. This makes it ideal to model protoplanetary disks. The version run by Ataiee et al. also includes calculations involving disk self-gravity and the inclusion of dust.

Ataiee et al. ran two different simulations. One involved disks that were purely made of gas, and with gas and dust. They simulated a planet orbiting the star in a fixed circular orbit. The simulation ran for up to 5000 planet orbits, depending on the viscosity. Using these simulations, they found the lowest possible planet mass which formed a radial pressure maximum, creating a pebble barrier. They varied the disk height and turbulent viscosity to see how these affected the PIM. In this paper, the PIM is reported as a normalized ratio between the planet’s mass and the star’s mass, as .

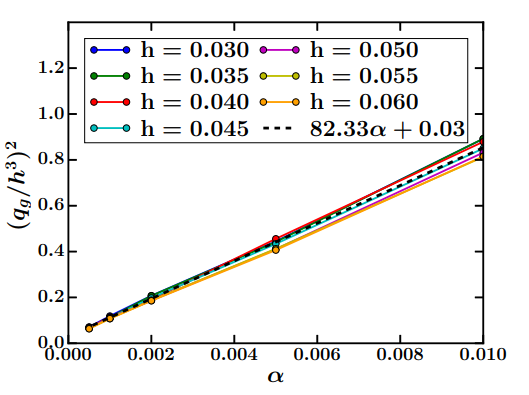
Figure 2:  This graph shows the relationship between the PIM and turbulent viscosity, as determined by a gas-only hydrodynamical simulation. Here, the PIM is reported as a ratio between the mass normalized to the star’s mass () and the aspect ratio (). From this, one can see that the PIM depends strongly on the scale height, but the gas turbulent viscosity () will also influence the PIM. The dashed line represents a fit for . Figure 2 in paper.

The results of these simulations, shown in Figure 2, reveal that while the PIM depends strongly on , it can also vary noticeably with . This is important, because the gas’s turbulent viscosity can vary greatly at different regions of planet formation. This can cause planets forming at different distances from the star to accrete different amounts of mass.

The next step was to look more closely at how dust affects the PIM. To do so, Ataiee et al. looked at some semi-analytical calculations to try to determine how the PIM also depended on the Stokes number of the dust and gas. This Stokes number is the ratio between the time it takes particles to reach the velocity of the gas and the timescale of turbulent fluctuations : . In doing so, they determine a correcting factor to maintain a pressure gradient in the gap. Otherwise, turbulence in the disk can give particles large enough velocities that they can get over the pressure bump. This means that the pressure will not be high enough to keep pebbles trapped.

The results found by Ataiee et al. are similar to other simulations. Depending on the scale height and aspect ratio of the simulations, Ataiee et al. report a difference of around 10 Earth masses compared to other studies. These other models make different assumptions and some are in 3 dimensions rather than 2. More work and observations will be needed to determine which models better describe what happens in the disk.

Conclusion

Although making a planet may seem like a simple prospect, things get a lot more complicated when you dive into the details. Once a planet has started to form, either due to core accretion or disk instability, the trapping of pebbles can prevent additional mass from reaching it. Therefore, there must be some other process which helps create larger planets, like gas giants.

Ataiee et al. have shown that the turbulence within the protoplanetary disk is an important factor in determining how large a planet can get before it stops accreting pebbles. Future work must be done to examine the stability of this pebble ring. If the ring has a very short lifetime, than the planet might experience periodic growth as the pressure bump is occasionally destroyed.

Although the trapping of pebbles could slow planetary formation, it could also produce observable effects. The pebbles will form a bright emission ring at millimeter and sub-millimeter wavelengths. Depending on the stability and lifetime of this ring, future observations of pebble rings in protoplanetary disks could be used to derive information about the conditions within the disk.

• About the Author

About Peter Sinclair

I'm a graduate student at the University of New Mexico. My hobbies include reading, cooking, and playing board and video games. You can find me on Twitter @Phiteros and on my blog, themodernpolymath.com.

Related posts:

Our Solar System: Another Planet or Another Disk? Habitable Moons at the Ice Line? Are Extrasolar Worlds More Likely to Be Water-rich? Nature’s Starships Vol. II – A Hitchhiker’s Guide to the Bloody Cold Beginnings