Authors: William H. Kinney, Sunny Vagnozzi and Luca Visinelli
First Author’s Institution: The Oskar Klein Centre for Cosmoparticle Physics, Department of Physics, Stockholm University, Sweden and Department of Physics, University at Buffalo, USA
Status: Open access on arXiv
What do zoos and swamplands have to do with Cosmology? There’s a zoo of possibilities for how inflation happened, and there’s a landscape of possible string theories surrounded by a swampland of implausible ones… and we need to find ways to narrow them down.
Inflation and String Theory
Inflation describes how the Universe expanded extremely rapidly within the first second of its existence. It explains and solves some big problems in Cosmology, for example the flatness problem and the horizon problem, so it’s one of the most popular theories for the early history of the Universe. However, inflation can only describe how things worked in the early Universe up to a certain energy scale (although we’re not sure exactly what that scale is), so ideally we’d like to find an overarching theory that is compatible with inflation, but that also tells us how things work at arbitrarily high energies.
String theory offers examples of such high-energy theories. However, for these candidates to be successful, the low-energy limit of such a theory needs to predict a well-defined inflationary model as well as explaining the high energy behaviour. Those that can do both are known as residing on the string ‘landscape’, and those that can’t are banished to the stringy ‘swampland’.
Today’s authors have added to the mix by claiming that theories that are happily on the string ‘landscape’ (and safe from the swampland) are inconsistent with current cosmological data that constrain theories of inflation.
How do we test inflation?
There are lots of models for exactly how inflation worked, and a popular way of distinguishing between them involves two key quantities that are predicted theoretically, that we can then go out and measure. They are known as the tensor-to-scalar ratio and the spectral index
. The quantity
is related to how many primordial gravitational waves were produced, and the quantity
measures how dense regions were distributed as a function of scale in the early Universe (it’s the gradient of the primordial power spectrum – see here for an explanation).
So far we have constrained these two quantities pretty well with Cosmic Microwave Background experiments such as Planck, and we know that we require and
. This means that for an inflationary model to be successful, it must predict values of
and
within these bounds. Figure 1 is an example of the zoo plot – it shows the predicted values of
and
for the zoo of potential inflationary theories. These are shown by the bold lines and shaded regions. For example, the purple shaded region represents the allowed values of
and
for the natural inflation model. The red, blue and grey egg-shaped regions are the allowed regions according to the Planck 2018 observational data. This means that the models whose predictions fall inside these red, blue and grey regions haven’t been ruled out by observations yet. Predictions that lie outside of these regions have been ruled out already.
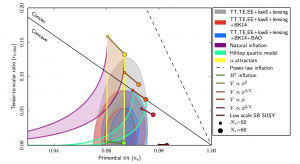
Figure 1: The zoo plot from the Planck 2018 results. The bold lines and shaded regions represent theoretical predictions for various inflation models, whilst the grey, red and blue egg-shaped regions show allowed values for and
according to the most recent data. Figure from Planck 2018 release.
The zoo plot and swampland avoidance
Now let’s look at what happens when we add constraints on string theory models to the zoo plot.
For a particular string theory model to avoid the swampland, a parameter that relates to inflation, , needs to be greater than 1.
Figure 2 is another plot of versus
with additional swampland conditions. The red regions show the allowed values according to current cosmological data (they use the slightly older Planck 2013 constraints which is why the allowed regions are slightly larger than in figure 1). Meanwhile, the blue regions show different values for
.
Only values of are compatible with the red regions that depict current data, as
would lie outside of the allowed red regions. This suggests that it’s not possible to avoid the swampland and respect the observational constraints simultaneously. This would mean that a string theory which successfully predicts inflation and explains the highest energies, can only predict a model of inflation that is already ruled out by observational data.
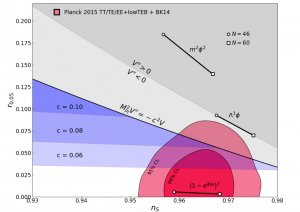
Figure 2: The blue regions show the allowed values of and
for different values of
. The red regions show the allowed values of
and
according to current data. Given that a successful high-energy theory requires
, there are no values of
and
that satisfy both high-energy theory requirements and current data. Figure from today’s paper.
If the conclusions of today’s paper are correct, it’s looking as though many high-energy theories are incompatible with current cosmological data. Unless inflation isn’t the correct picture for how the Universe expanded, the ‘successful’ string theories predict inflationary theories that are already ruled out. The authors show that there are a few models that might still work, and with multiple papers being published on this topic in recent weeks, it’ll be an exciting discussion to keep track of.
Cover image found here.



Thank you for such a concise, interesting explanation.
Actually, string theory is not the only theory that has problems with the de Sitter space and the cosmological constant. In Starobinsky’s model of inflation the de Sitter phase of expansion is driven by the quantum conformal anomaly as an alternative to scalar field driven inflation. According to this model, the de Sitter solution is unstable, but could be long-lived. This model was expanded and developed by Vilenkin (Phys Rev D32, 2511, 1985), and Hawking, Hertog & Reall (hep-th/0010232v4). In particular, Hawking et al, argued that while convenient models of scalar field driven inflation disregard the effect of other fields in the universe, the quantum conformal anomaly provides an additional contribution to the cosmological constant during inflation. Later on Ford, Tomboulis, Schutzhold, Antoniadis, Mottola and most recently Koksma, Polyakov, Netto, Matsu, based on QFT reasoning, showed that quantum gravitational effects in the early universe destabilize the de Sitter space eventually making it incompatible with any consistent theory of quantum gravity. The Swampland conjencture is probably the last nail in the coffin of the de Sitter space.