Authors: Elaad Applebaum, Alyson M. Brooks, Thomas R. Quinn, Charlotte R. Christensen
First Author’s Institution: Rutgers University, NJ
Status: Submitted to MNRAS; open access on arXiv
Introduction: Where the small galaxies at? You bad!
Dwarf galaxies are little, but they pack a big punch—they’re among the most extreme and diverse environments in the universe. Also, our current understanding of structure formation in the universe (called ΛCDM) suggests that these low-mass galaxies formed first and built up into larger structures like our own Milky Way. This means that understanding the formation of dwarf galaxies can tell us a lot about how overall structures form in the universe.
Computational models of dwarf galaxies have become realistic enough to be able to match most theoretical predictions. The highest-resolution models are now pushing to smaller and smaller galaxy masses—into the regime of the “ultra-faint dwarf galaxies” (UFDs, which we’ll define as galaxies with stellar masses solar masses). But because UFDs are such extreme environments, some of the standard assumptions about typical galaxy formation break down.
Today’s paper by Applebaum et al. focuses on one of these assumptions, arguably the most ubiquitous of all: the stellar initial mass function (IMF). This function describes the relative numbers of stars that are born at different masses. Why does this matter? It turns out that assumptions about the IMF underpin nearly all of our observations of galaxy properties and our theoretical models of galaxy evolution. So questions about the IMF—its exact shape, whether or not it’s the same in all galaxies, etc.–are actually incredibly important areas of active research. And as the authors of today’s paper discover, the IMF can have huge consequences in UFDs.
You don’t want no problem with the IMF
It’s been known for a while that in low-mass galaxies, the IMF is not well-sampled. In other words, because so few stars form in these small systems, not enough stars are born to fully populate the IMF.
How does this work? For example, let’s assume that the IMF predicts that only 1 out of every 100 stars born is a high-mass star (~10 solar masses). If 10,000 stars are born, then we expect around 100 massive stars. The IMF is a probability distribution, so this isn’t an exact prediction; the true number of massive stars will fluctuate in a “stochastic” (i.e., random) way. But the fluctuations aren’t very large compared to the actual number: if there are, say, 90 high-mass stars instead of 100 stars, the difference of 10 stars is relatively small. On the other hand, if only 100 stars are born, only 1 high-mass star is expected. Random fluctuations could easily produce a few high-mass stars, doubling or tripling the expected number of stars. Or they could just as easily produce no high-mass stars at all.
This difference can have a huge effect on the overall properties of a galaxy, because massive stars go out with a bang as core-collapse supernovae. These intense explosions inject energy and momentum (which we call “feedback”) into a galaxy. Feedback “regulates” star formation by heating the gas in a galaxy and preventing it from collapsing to form stars. In low-mass galaxies, which aren’t as tightly bound by gravity, even a relatively small amount of feedback can produce enough momentum to eject the interstellar medium from the galaxy entirely! So fluctuations in the small number of massive stars can cause huge overall fluctuations in feedback processes.
One two, one two, supernovae on beat
It’s surprisingly difficult to model this kind of stochastic feedback in galaxy simulations. For a long time, most models just assumed some constant rate of energy injection; it’s only recently that simulations have been able to consider discrete feedback events. This is a hard thing to do mostly because of the huge range of scales that have to be simulated. Stars are incredibly small compared to entire galaxies. Simulating the physics of individual stars is basically impossible, so “cosmological” simulations (i.e., simulations that encompass a volume much larger than a single galaxy) instead track “star particles” consisting of thousands of stars.
The authors of today’s paper manage to implement a stochastic IMF into the star particles of their cosmological simulation. Every time they form a star particle, they draw randomly from the IMF until the desired mass of the star particle is reached. Then the number of high-mass stars “drawn” is used to calculate how much feedback energy is injected (and when to inject it). This stochastic sampling leads to long periods without any feedback interspersed with short intervals of much stronger feedback, which looks very different from the near-constant low-level feedback produced by the usual assumption of a fully-populated “continuous” IMF (Figure 1).
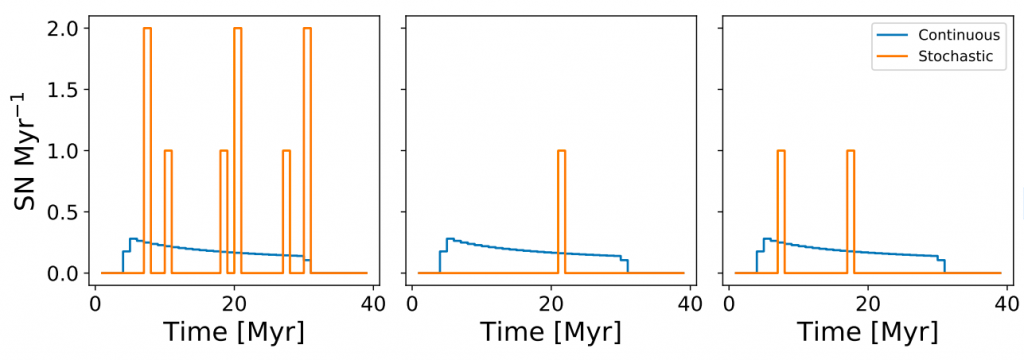
Figure 1. The supernova rate (in units of number per Myr) as a function of time for three different star particles with different IMF prescriptions. The stochastic IMF (orange) shows long periods of no supernovae, interspersed with intervals of lots of supernovae. The continuous IMF (blue) shows a low level of near-constant supernova rates. Figure 2 from the paper.
What effect does this have on the actual properties of galaxies, especially UFDs? Applebaum et al. find that UFD galaxies modeled using the stochastic IMF are worse at forming stars than the galaxies modeled using the continuous IMF, so they have lower stellar masses (Figure 2, left). This is because the stochastic IMF leads to bursty feedback (Figure 2, right). The supernovae in the stochastic model tend to be clustered together in time, which more effectively heats the gas in the UFD and prevents it from forming stars.
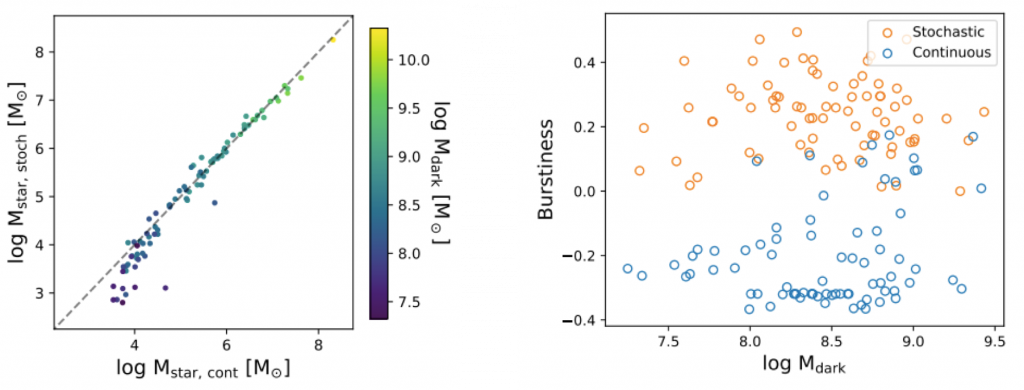
Figure 2. (Left) The stellar mass computed using the stochastic IMF (y-axis) compared to the stellar mass computed using the continuous IMF (x-axis). Each point is a galaxy, colored by its dark matter halo mass. For low-mass UFD galaxies, the stochastic IMF predicts lower stellar masses than the continuous IMF. Figure 4 from the paper. (Right) The “burstiness” of the supernova rate as a function of dark matter halo mass. “Burstiness” B is defined so that a uniform distribution has B=-1, an exponential distribution has B=0, and a Dirac delta function has B=1. The stochastic IMF (orange) model is much burstier than the continuous IMF (blue) model. Figure 6 from the paper.
Conclusion: We don’t do the same feedback no more
Why is this result interesting? Well, more accurate predictions of star formation are important for answering many open questions about UFDs: for instance, what shuts off (“quenches”) star formation in UFDs? Do stars in UFDs play a role in helping reionize the universe? The method described in this paper also provides a way to track individual high-mass stars. This might eventually let us do cool things like predict the number of stellar remnant events–including neutron star mergers and other gravitational wave events.
But on a deeper level, this paper is also just interesting because it’s a good reminder that we can’t always rely on simple assumptions. Our simulations are only as good as the physics we put into them, so as our computational power improves, we need to start taking the small details into account—especially when we think about UFDs, the smallest systems in the universe.
(Apologies to Chance the Rapper for adapting his lyrics to terrible puns.)