Authors: Cecilia Payne (later Payne-Gaposchkin)
First Author’s Institution: Radcliffe College (now part of Harvard)
Status: Open access
Introduction
“The universe is mostly hydrogen and ignorance,” goes a version of one of my favorite quotes. It’s true: we’re pretty ignorant about dark energy (~70% of the universe) and dark matter (~26% of the universe). Of the matter that we do know about (the “baryonic matter”), about 3/4 is hydrogen!
Today, it’s an accepted fact that nearly all stars are predominantly made of hydrogen. But how do we know this? Enter Cecilia Payne, whose PhD thesis in 1925 changed the way we understand the composition of the universe. Her thesis tied together two seemingly disparate elements—a theory by Indian physicist Meghnad Saha, and the system used to classify stars by Annie Jump Cannon and other women astronomers—into one beautiful work that explained the stuff of stars.
Payne’s thesis was written as a book with three parts, which we’ll go through here.
Part I. What we knew
In 1925, astronomers actually knew quite a lot about stellar spectra, and Payne’s thesis begins by summarizing the state of knowledge at the time.
Observationally, hundreds of thousands of stellar spectra had been measured and classified in the Henry Draper Catalogue. This classification scheme (which was developed and implemented by Annie Jump Cannon, Williamina Fleming, and Antonia Maury, among others) sorted stars by the relative intensity of various spectral lines. In particular, the system initially classified stars according to the strength of the Balmer absorption lines from hydrogen: A stars had the strongest Balmer lines, then B stars had the next strongest, and so on.
On the theoretical end, the physical mechanisms behind most of the features in stellar spectra (Figure 1) were fairly well understood. In 1925, it was known that a star mostly behaves like a blackbody, producing an underlying continuum of radiation. However, elements in the star’s atmosphere absorb some of the light, producing spectral lines. The exact wavelengths of these lines are determined by the energies of electronic transitions; an atom can only absorb a photon if the photon has the right amount of energy needed to excite one of its electrons. The Balmer absorption lines, for instance, are produced by electrons transitioning from the second energy level of hydrogen to higher energy levels.
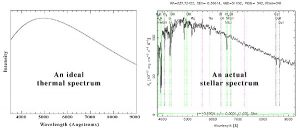
Figure 1. A perfect blackbody spectrum (left) and an actual stellar spectrum (right). Although the overall shape (the continuum) of the stellar spectrum looks like a blackbody, there are lots of spectral lines (marked with shaded regions) caused by elements in the star’s atmosphere.
Part II. The theory of thermal ionization
Based on this prior knowledge, it became clear that the relative intensities of spectral lines are strongly dependent on the temperature of a star. How does this temperature dependence work? Each spectral line has a specific temperature at which its intensity peaks. If a star is much colder or much hotter than this temperature, either the star won’t produce enough photons with the right energy to excite electrons, or its atoms won’t have enough electrons in the right state to be excited—so the spectral line will be weak.
For example, stars with temperatures of approximately 10,000K have the strongest hydrogen Balmer lines. This is because stars much cooler than this have most of their electrons in the lowest energy level, rather than the second energy level. Since Balmer absorption lines are produced when electrons in the second energy level are excited, this leads to weak Balmer lines. But stars much hotter than 10,000K are hot enough to have ionized most of their hydrogen, so there are no bound electrons that can be excited—leading again to weak or nonexistent Balmer lines.
To quantify this kind of effect, we therefore need to know how temperature affects the number of atoms that are in a suitable state to absorb photons. To do this, Payne (following in the footsteps of Ralph Fowler and Arthur Milne) used the theory of thermal ionization, which was first applied to stellar atmospheres by physicist Meghnad Saha. This theory is best encapsulated in the Saha ionization equation: given an element and a temperature, this equation tells you the fraction of atoms in a given ionization state.
Payne used this kind of analysis (also correcting for some more complicated factors, like differences in pressure caused by different abundances of elements) to assign the spectral classes to temperatures. The temperature scale published in her thesis is almost exactly the same as the one we use today (Figure 2)!

Figure 2. Cecilia Payne’s derived temperature scale (left) and the accepted temperature scale used today (right; credit: Wikipedia).
Part III. Putting it together
Payne then took her analysis a step further and did something truly revolutionary: she flipped the Saha equation around and used it to figure out the relative abundances of elements in stars.
How does this work? Instead of considering when a spectral line reaches maximum intensity, Payne considered the maximum temperature at which the line appears. At
, nearly all of the atoms are ionized, and only some small fraction of the atoms are in the right state to absorb photons. Using the Saha equation, Payne was able to compute this fraction:
.
However, since the line disappears at temperatures above , the number of atoms able to absorb photons at
must be the minimum number of atoms needed to produce a spectral line at all. Payne assumed that for all chemical elements, this minimum number of atoms must be about the same (i.e., that
is constant for all elements, which is an okay assumption to first order). This allowed her to compute relative abundances
for the most common stellar elements.
Payne found that most of the elements in stars had roughly the same relative abundance as the elements in the Earth’s crust (this makes sense given what we know today, since the Earth and the Sun were formed out of the same material). But hydrogen and helium were exceptions—in fact, they were around a million times more abundant than some of the other elements! This isn’t terribly far off from what we know today (Figure 3).
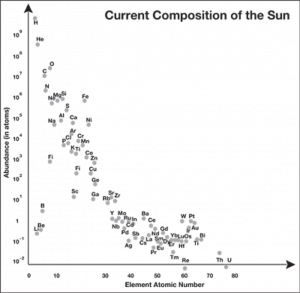
Figure 3. The relative abundance of elements in the Sun. Note that the y-axis is a logarithmic scale. (Source)
Conclusion
When Payne’s thesis was reviewed, Henry Norris Russell (of Hertzsprung-Russell fame) was skeptical of its conclusion that hydrogen and helium were unusually abundant in the stars. Russell convinced Payne to soften her conclusion, and the published thesis eventually read that “the actual values [of H and He abundances] derived […] are regarded as spurious.”
Only four years later, Russell came to this same conclusion using a slightly different method. (Unsurprisingly, this time he actually believed it.) However, Payne’s thesis still remains the first conclusive evidence that hydrogen is the most abundant element in the universe.
Today, astronomers around the world continue to use spectra to measure the abundances of elements in stars. Our techniques are getting better and better; one recently-published method even uses a machine learning algorithm called an artificial neural network to determine stellar abundances from spectra! The name of this method? The Payne—named “in appreciation of Cecilia Payne-Gaposchkin’s ground-breaking work on physical spectral models.”


I remember, some decades ago, Otto Struve calling her thesis the greatest PhD thesis in the history of astronomy.. Stillas true today!!
Thank you for reminding us of one of the seminal works in modern astronomy!