Title: Electromagnetic counterparts of black hole-neutron star mergers: dependence on the neutron star properties
Authors: C. Barbieri, O. S. Salafia, A. Perego, M. Colpi, G. Ghirlanda
First Author’s Institutions: Università degli Studi di Milano-Bicocca, Milano, Italy; INFN – Sezione di Milano-Bicocca, Milano, Italy
Status: Open access on ArXiv
Recent gravitational wave (GW) detections have generated a lot of excitement around the merger of neutron stars (NSs) with black holes (BHs). However, while the first detection of merging neutron stars was a treasure trove of observational data both gravitational and electromagnetic, all BH-NS merger candidates so far remain shrouded in darkness. No ‘smoking gun’ electromagnetic (EM) counterpart to a NS-BH merger event has been observed yet. Joint GW-EM detections are important because different messengers carry different pieces of information, helping us paint a coherent picture of the source.
Perhaps this isn’t shocking: a BH-NS merger may not produce any EM counterpart at all, let alone one that’s bright enough to observe! The BH can simply swallow the NS whole, without the telltale kilonova glow.
So when can we expect to find a counterpart? And would these kilonovae look very different from the ones produced in binary NS mergers? Questions abound regarding the nature of the EM emission from BH-NS mergers. Today’s paper investigates the EM counterparts of these events for a range of binary properties, revealing interesting (and sometimes subtle!) patterns.
What gives a merger its glow?
The EM emission from BH-NS mergers depends on four main parameters: the mass of the NS (MNS), the tidal deformability of the NS (ΛNS, describes how much a body is deformed by tidal forces), the mass of the BH (MBH), and the spin of the BH (χBH). Only some combinations of these four parameters produce an EM counterpart. This is because to produce a counterpart, the NS must be disrupted, releasing neutron-rich material. Whether disruption occurs at all depends on the relative position of the BH innermost stable circular orbit (ISCO) and the distance at which the BH is able to tidally disrupt the NS, i.e., the tidal disruption radius.
If the tidal disruption radius is less than the ISCO radius, the NS plunges into the BH, leaving nothing behind. If not, the NS gets disrupted and some of the material settles into an accretion disc around the BH – a potential central engine for short duration gamma-ray bursts (GRBs). Some material gets flung out into space as very neutron-rich “dynamical ejecta” which forms r-process elements. Yet more material, of uncertain mass and composition, is ejected from the accretion disc through a variety of mechanisms. The radioactive isotopes created in the ejected material produce a transient (our “kilonova” counterpart) when they decay. So, to guess whether an EM counterpart will be produced in a BH-NS merger, we can compare the ISCO radius with the tidal disruption radius.
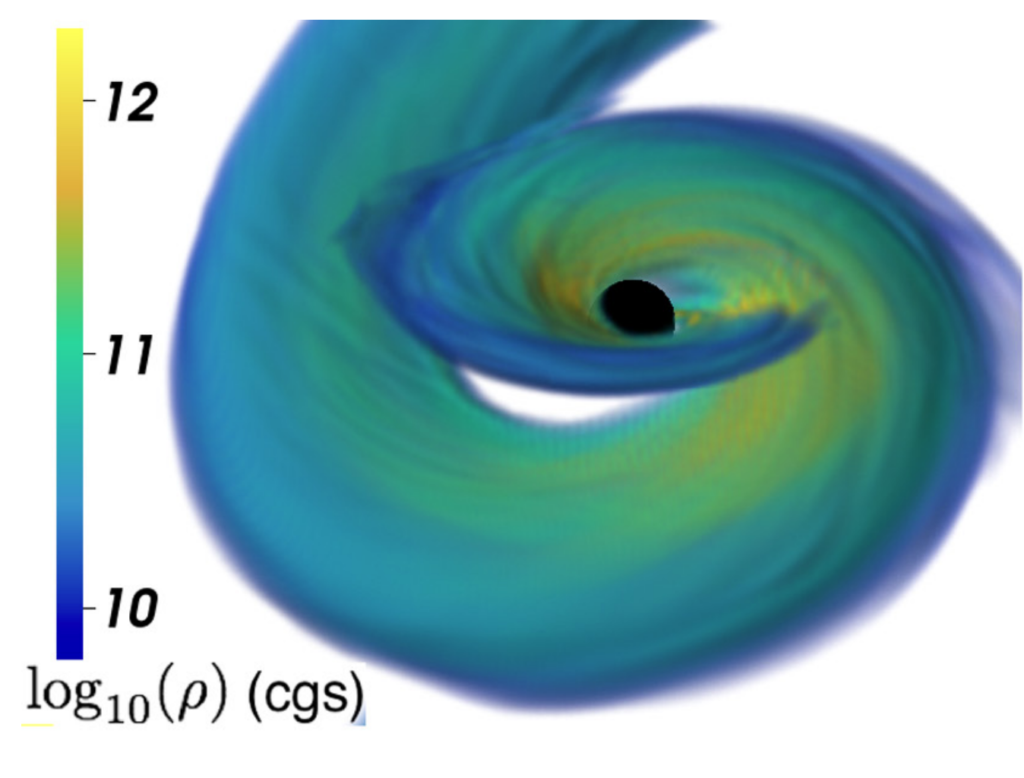
Simulation shows the baryon density in the aftermath of a NS-BH merger. The disc is beginning to circularize. (Credit: Classical and Quantum Gravity)
However, the ISCO radius itself depends on the BH mass and spin, while the tidal disruption radius depends on the BH mass as well as the mass and radius of the NS. The relationship between the mass and radius of a NS is not arbitrary either – it follows from the properties of dense nuclear matter as described by the NS equation of state (EOS). For a given MNS, a “softer” EOS leads to NSs with smaller radius, and smaller tidal deformability, than a “stiffer” EOS. This is how we end up with our four key parameters: (MNS, ΛNS, MBH, χBH).
Dependence on BH properties
Let’s now take a look at what happens if you fix the NS parameters (MNS, ΛNS) and vary the BH parameters (MBH, χBH). From Figure 1, we see that lower BH mass and/or higher BH spin leads to larger dynamical ejecta and accretion disc masses. This suggests that binaries with low mass ratios (MBH/MNS) and high BH spins are favorable for tidal disruption.
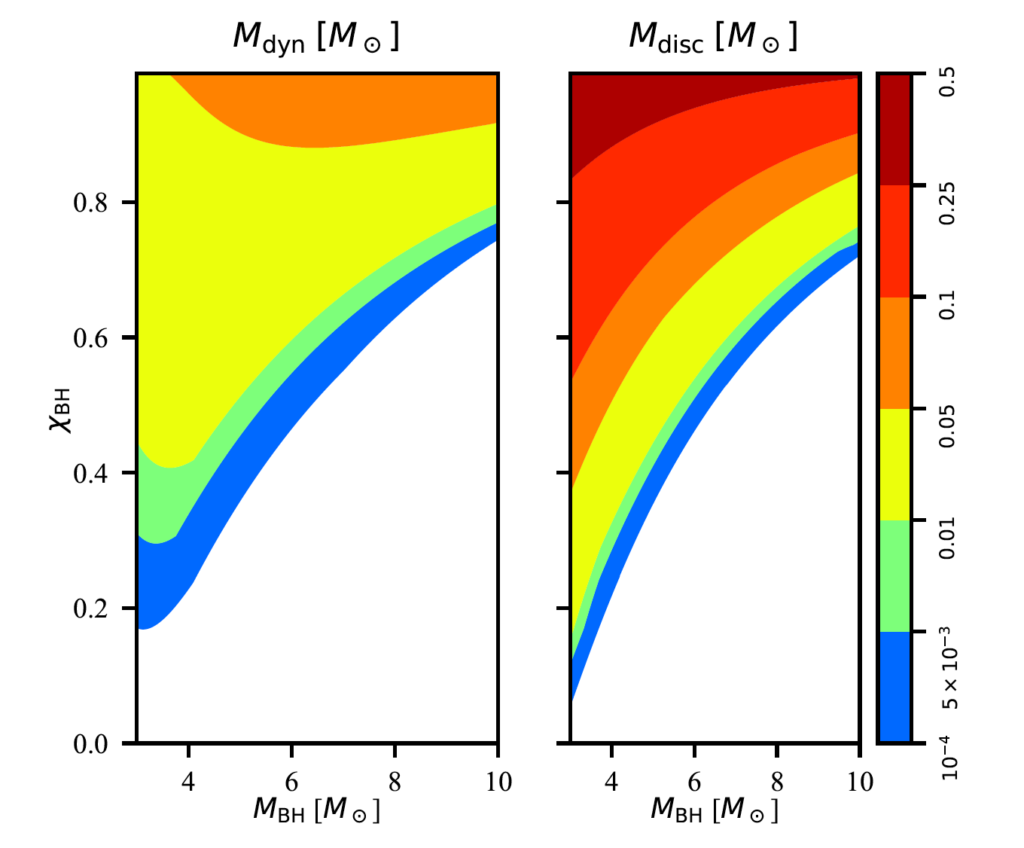
Fig 1. Dynamical ejecta (left) and disc masses (right) assuming a 1.4 solar mass NS and ΛNS=330. Color coding gives the estimated mass in solar masses over the MBH – χBH parameter space. White regions correspond to the NS plunging into the BH. Figure 2 in the paper.
Dependence on NS properties
The primary focus of today’s paper, however, is on the NS parameters: MNS and ΛNS. The authors fix the BH mass and spin, choosing from 2 values of MBH and 3 values of χBH. Then, varying (MNS, ΛNS) over a wide range, they examine how the dynamical ejecta and disc masses depend on the NS properties.
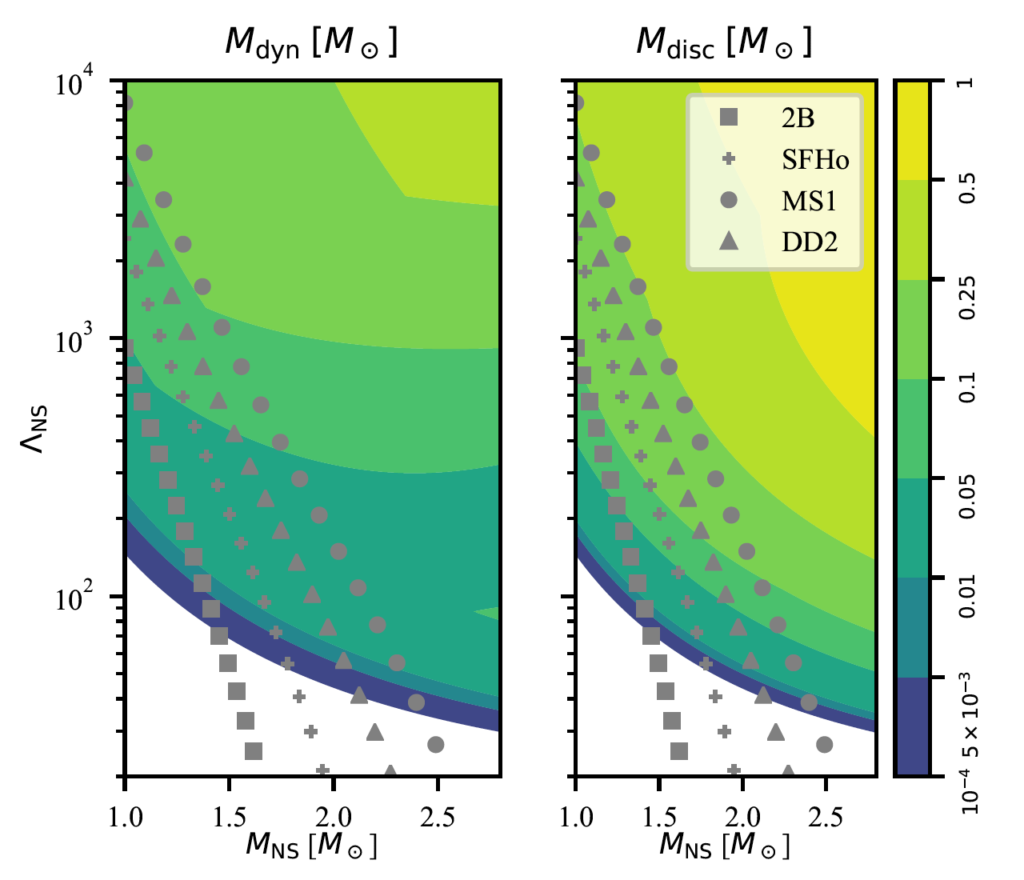
Fig 2. Dynamical ejecta (left) and disc masses (right) assuming a 6 solar mass BH and χBH=0.8. Color coding gives the estimated mass in solar masses over the MNS – ΛNS parameter space. Grey symbols correspond to the MNS – ΛNS relation for different equations of state. Figure 6 in the paper.
Figure 2 shows the result of their study for a fixed (MBH, χBH). If we examine each NS parameter by itself, it appears that higher MNS and higher ΛNS values favor NS disruption. However, it’s important to remember that not every combination of MNS and ΛNS makes physical sense. It would be more meaningful to pick a few physically motivated EOSs and examine the allowed combinations only. The authors do exactly this and find that the optimal binaries producing massive dynamical ejecta and discs involve low mass NSs, not high!
Shining bright!
Based on the ejecta (and additional) estimates, the authors calculate kilonova and GRB afterglow lightcurves using semi-analytical models. They study how the lightcurves depend on the NS mass and its deformability. One such calculation is shown in Figure 3. In general, for a given NS mass, larger ΛNS produces brighter kilonovae and afterglows. If we fix ΛNS instead, then larger NS masses result in brighter kilonovae and afterglows.
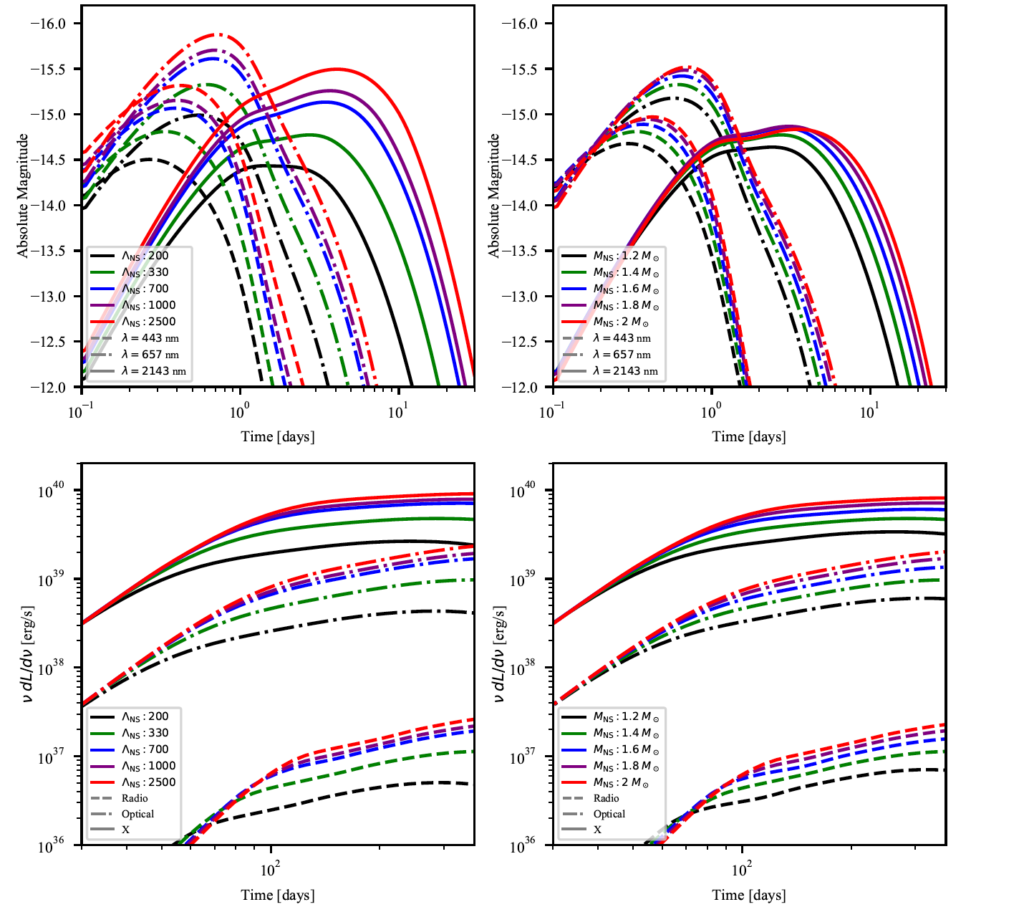
Fig 3. Dependence of kilonova (top) and GRB afterglow (bottom) lightcurves on NS tidal deformability (left, given a 1.4 solar mass NS) and NS mass (right, given ΛNS=330). The BH mass is 3 solar masses and χBH=0.5. Different linestyles correspond to different wavelengths or frequencies (see legend). Figure 8 in the paper.
Same or different?
Finally, the authors compare their kilonova predictions to AT2017gfo, the kilonova associated with the binary NS merger event – GW170817 – and find that they are able to reproduce the r and K band magnitudes quite well. However, the BH-NS kilonovae are always dimmer in the B band than the observed kilonova! The reason could be that reproducing these B band observations requires relatively high electron-fraction material, which is achieved more readily in NS-NS mergers compared to BH-NS mergers. The authors conclude that B band observations of kilonovae could help us distinguish a NS-NS merger from a BH-NS merger, even in the absence of gravitational wave data!
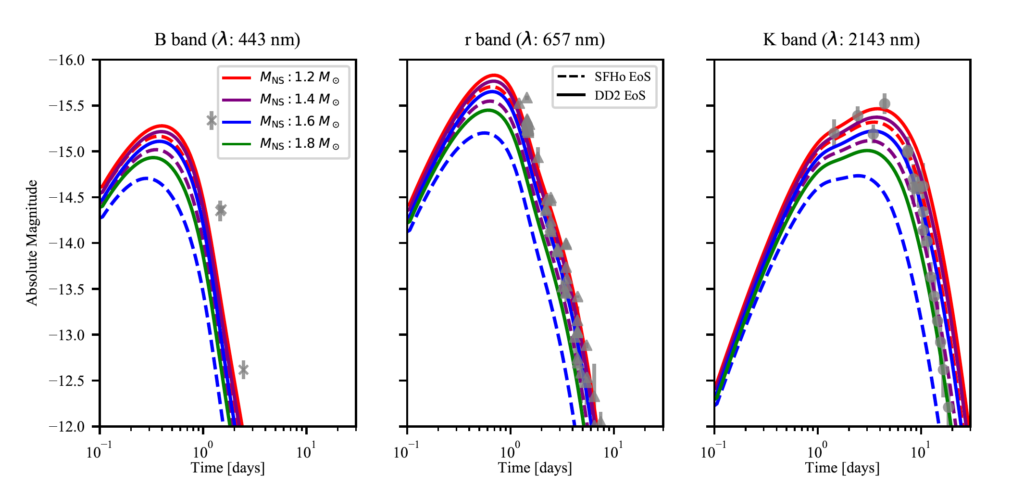
Fig 4. Kilonova lightcurves for different NS masses and EOSs. The gray points show observation data for the kilonova counterpart of GW170817. The BH mass is 6 solar masses and χBH =0.8. Figure 15 in the paper.
There is a lot of exciting multimessenger science to be done with BH-NS mergers in the next few decades and studies like this are extremely valuable for understanding the range of behavior one can expect from various sources of interest. We are steadily collecting pieces of a huge cosmic puzzle, one observation at a time, whether gravitational or electromagnetic. Putting these pieces together into a cohesive theoretical picture is a lofty goal, but one that will lead to many discoveries and (I’m willing to bet on this) even more surprises. Stay tuned!