Authors: Andrew J. Hesselbrock and David A. Minton
First Author’s Institution: Purdue University
Status: Published in The Astronomical Journal [open access]
The number of known ring-bearing objects in the solar system continues to expand. Once limited to Saturn, the list added all four giant planets in the 1970s and 80s. More recently, stellar occultation observations have found rings around minor planets Chariklo, Chiron, and Haumea.
Unlike moons, most ring systems are never alone. The existence of satellites and rings alongside one another creates complex dynamics that shape the course of evolution for both objects. Beyond that, there are outside influences, such as close encounters with scattered Kuiper Belt objects (which happened to Neptune) or giant impacts (which happened to Earth) that vastly increase the number of possible evolution tracks.
The authors of this paper designed a generalized model of ring and satellite co-evolution designed to be simple to comprehend and applicable to the solar system.
Know Your Limits
There are four primary boundaries for every satellite in orbit. What happens when satellites interact with these boundaries determines much of the way the system will evolve.
Tidal forces on a satellite arise due to the difference in gravitational pull from the planet on the near versus far side of the satellite. At the Roche limit, the strength of the tidal force on the near side of the satellite equals the strength of gravity holding the surface intact. Any satellite that ventures beyond the Roche limit will be torn apart by tidal forces and smeared out into a ring, as shown in Figure 1.
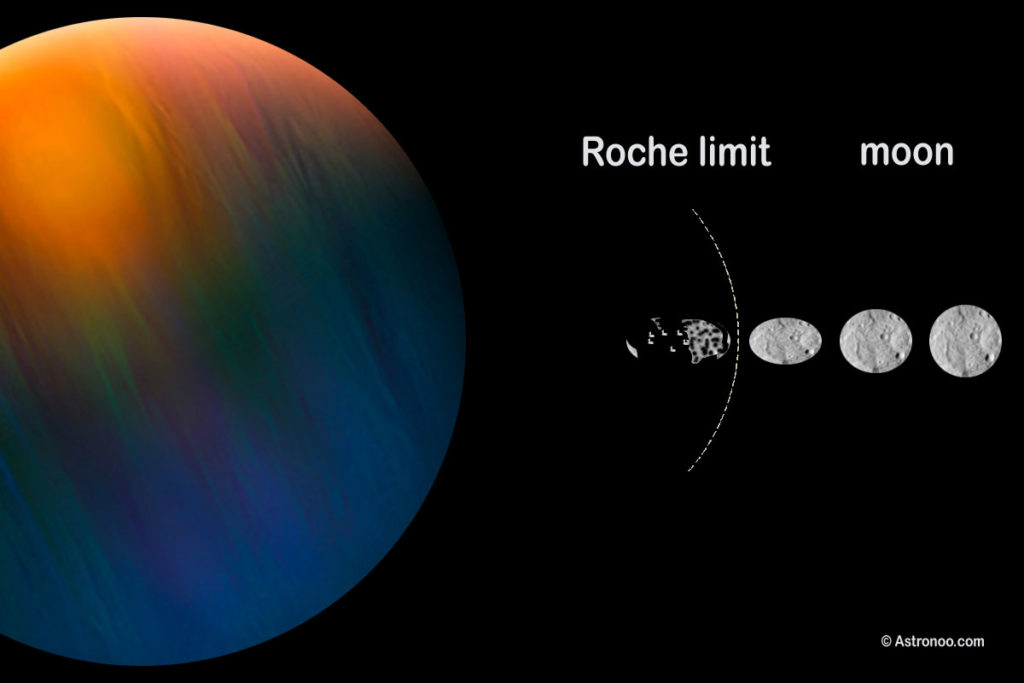
There are, in fact, two Roche limits. The fluid Roche limit (FRL) is for loosely-held-together satellites and is farther from the planet because it is easier to pull pieces of a fluid apart. The rigid Roche limit (RRL) applies to solid bodies like the Moon, that have to get closer to the planet before they break apart.
Tidal forces have the overall effect of pulling a satellite toward its host planet but that does not mean it will come crashing down. When a satellite and a ring both orbit a planet, they can exchange angular momentum through Lindblad torques. Lindblad torques are density waves in the rings caused by resonances in the orbits—they balance the tidal forces and push the satellite farther away.
There is a maximum boundary to which the Lindblad torque can push a satellite and is denoted aLind in this paper. In order to keep a satellite in orbit, there must be a balance between tidal and Lindblad torques, otherwise the satellite will either break apart or be lost to space permanently.
The last boundary for any satellite is the synchronous orbit (asynch), which is the distance where the satellite orbits at the same rate as the rotation of the planet. Satellites in geosynchronous orbit (around the Earth) are used for communication because they are always directly above ground receivers. Synchronous orbit is extremely stable for a satellite because the tidal bulge on the planet caused by the satellite is stationary in the reference frame of the satellite. The result is no torque on the satellite that could severely disturb its orbit.
Three Regimes of Satellite Evolution
The primary innovation of this paper is being able to take complex math for a satellite-ring coupled system and turn it into three understandable regimes: “Boomerang,” “Slingshot,” and “Torque-dependent.”
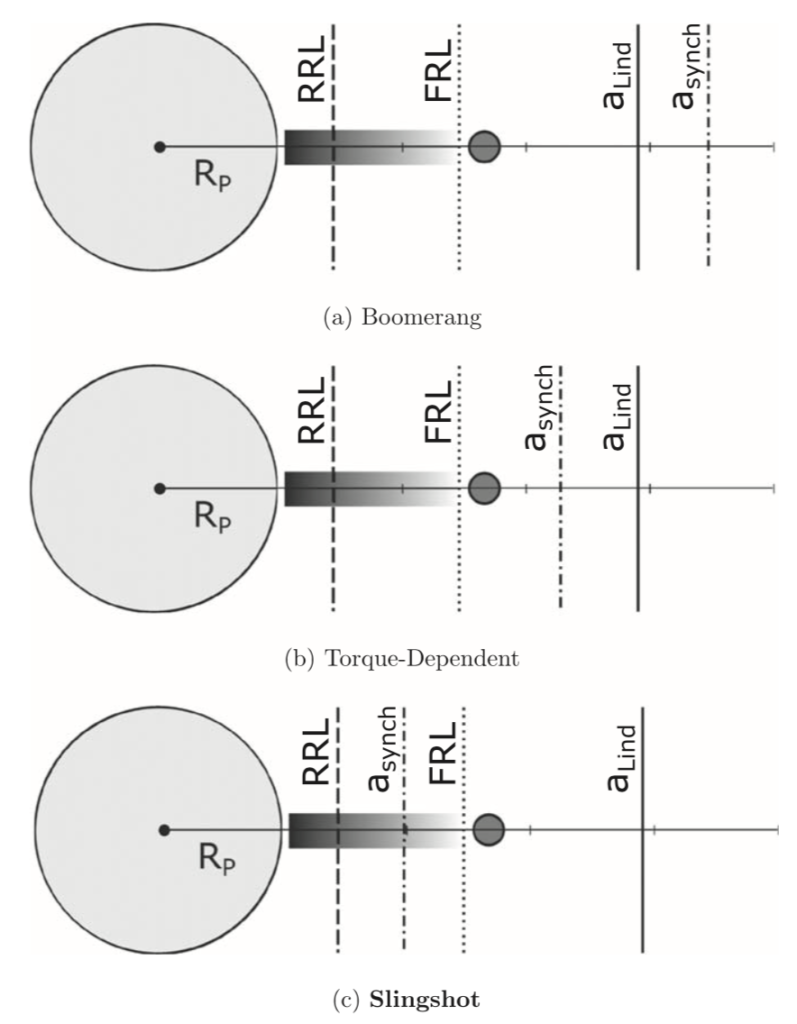
Figure 2 shows the orientation of each regime. In the Boomerang regime, asynch is beyond aLind, meaning the satellite wants to but can never get out to the stable, synchronous orbit. The Lindblad torques initially try to push the satellite out but eventually lose to tidal forces that drag the satellite all the way beyond the Roche limit.
At this point, some of the satellite breaks apart into a ring, which causes Lindblad torques to increase and the remaining satellite gets pushed back beyond the Roche limit. Like a boomerang, the satellite oscillates back and forth potentially for billions of years.
The Slingshot regime occurs when the synchronous point is within the fluid Roche limit, meaning there is no permanently stable orbit for a satellite. At the outer edge of the rings, some satellites may form from the ring material, but they are driven away from the planet by strong Lindblad torques, all the way to aLind. Any satellites that form from the rings are slingshot away from the planet forever.
The Torque-dependent regime is the middle-ground between Boomerang and Slingshot. The synchronous point is between the Roche limit and aLind, meaning the satellite can find a stable orbit depending on the strength of the torques acting on it.
Applications of the Classification
The authors apply their new satellite classification scheme to the solar system, as shown in Figure 3. The regimes are determined by the rotation period of the planet (which sets the synchronous point) and the density of the satellite (which sets the Roche limit and aLind).
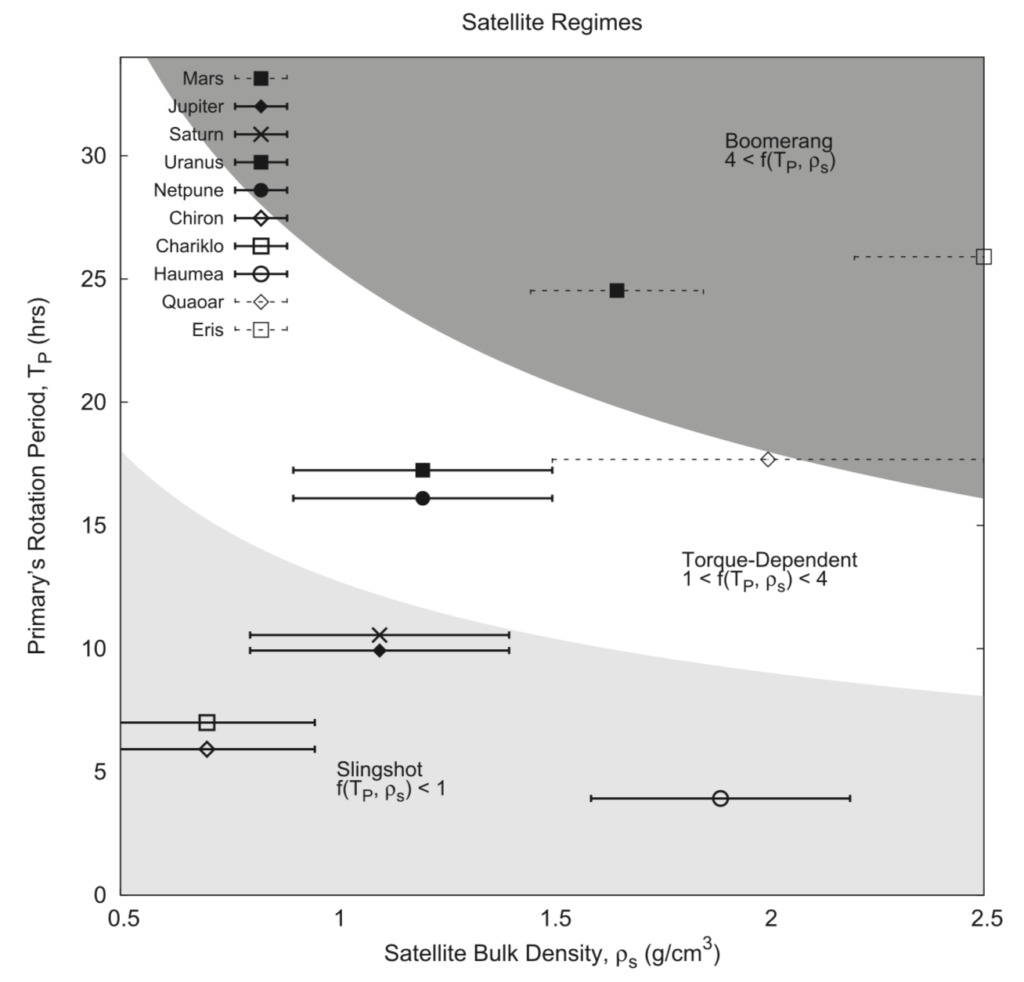
Mars is in the Boomerang regime and the authors believe that its moon Phoebos formed from a disk and will eventually form a disk again once it boomerangs back toward Mars.
Jupiter and Saturn are in the Slingshot regime because they rotate very fast, which puts their synchronous orbits too close for a satellite to survive. As satellites form from the outer rings of either planet, they get slingshotted into much more distant orbits.
Uranus and Neptune are in the Torque-dependent regime, meaning the stability of their satellites depends on the balance between Lindblad and tidal forces. One valuable use of this classification system is to look for exoplanets like Uranus, whose massive moon Miranda prevents smaller moons from reaching stable orbits. If exoplanets are observed to be in the Torque-dependent regime, it would be likely that they would have satellites and/or rings, which could then be identified.
The authors of this paper achieved two laudable goals. They created a satellite-ring schema that captures the important behavior in a complex system while preserving accuracy and completeness of the detailed math behind it.