This guest post was written by Sai Zhai, a first-year graduate student at Nanjing University, where she studies the formation and evolution of galaxies. In her spare time, she enjoys running and traveling with friends. The post was written in conjunction with an assignment in the Astronomical Literature Reading and Writing class taught by Professor Zhi-Yu Zhang.
Title: Detection of the Schwarzschild precession in the orbit of the star S2 near the Galactic centre massive black hole
Authors: GRAVITY Collaboration
Status: Accepted to A&A, open access on arXiv
Over many decades, Einstein’s theory of general relativity (GR) has been confirmed by multiple tests, including the precession of Mercury’s orbit, emissions from the double pulsar PSR J0737−3039, and gravitational waves detected by the Laser Interferometer Gravitational-Wave Observatory (LIGO).
Theoretically, GR predicts the existence of a black hole in the center of our galaxy. There is a lot of evidence showing that galaxies host massive central black holes, such as the relativistically broadened, redshifted iron Kα emission line seen in nearby Seyfert galaxies, high resolution millimeter imaging from the Event Horizon Telescope (EHT), and the atypical movements of stars close to the black hole candidate at the center of the Milky Way. In the last case, the precession of a star’s pericenter angle caused by the central supermassive black hole is called Schwarzschild precession (SP).

However, the SP of the star’s pericenter angle is hard to measure because it is so small. This measurement becomes even harder for the galaxies that are far away from us. Thus, the best place to observe this phenomenon is in the center of the Milky Way.
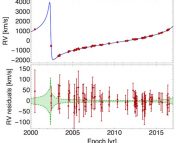
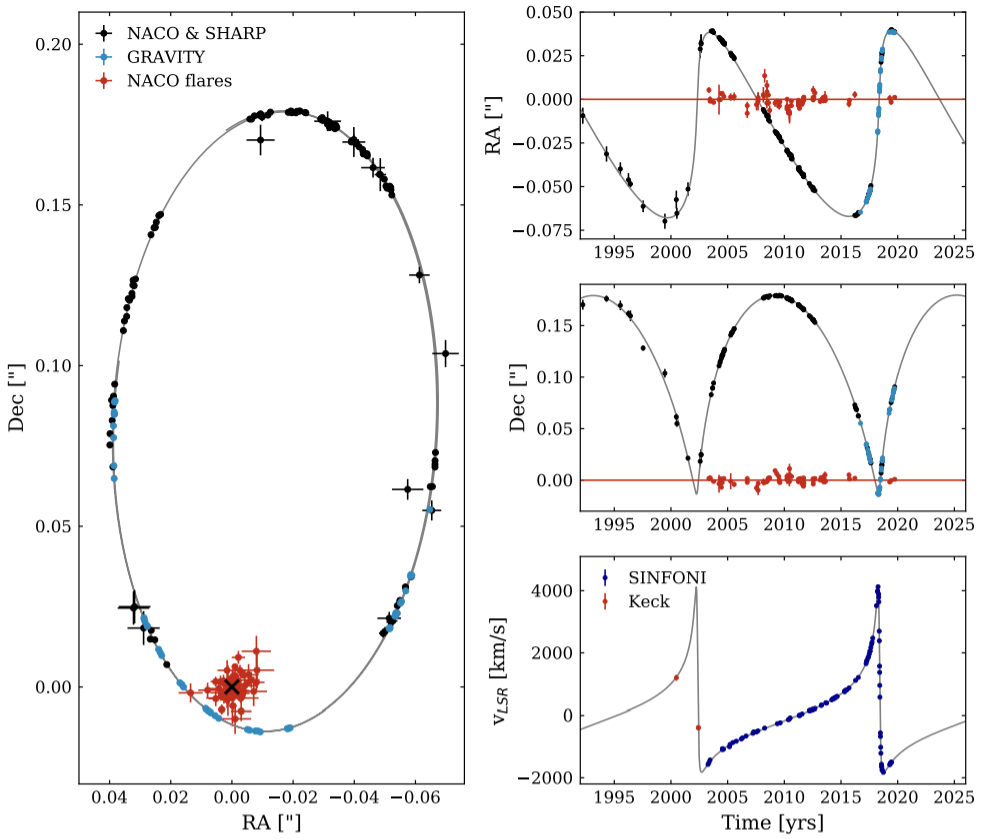
Sgr A* is the nearest supermassive black hole candidate to us. It is surrounded by a star cluster. Among those stars, S2 is the second closest star to the galactic center. Observations of S2’s orbit taken from 1992 to 2019 supplied enough imaging and spectroscopic data to measure the precession of S2 in high detail. Because of precession, S2 cannot return to its “original position” after one orbital period. Only the pericenter (the star’s position when it’s at its nearest to Sgr A*)and the apocenter (the furthest the star gets from Sgr A*) can be distinguished, and since the pericenter is easier to observe, precession studies tend to focus on the pericenter. During the observation period, S2 passed the pericenter twice, once on May 1, 2002, and again on May 19, 2018.
The paper discussed here describes the first detection of Schwarzschild precession in the orbit of the star S2.
One of the challenges of detecting SP is accurately measuring the separation between Sgr A* and S2. Luckily, GRAVITY, a four-telescope instrument on the Very Large Telescope Interferometer (VLTI), has the superb ability to measure positions of objects on the sky with high accuracy. It also helps to eliminate the effects of orbit disturbances from nearby stars. From 2017 to 2019, GRAVITY observed the orbital motion of S2, including when S2 passed through the pericenter. With a precise definition of the reference frame, it is possible to detect the SP of the star S2.
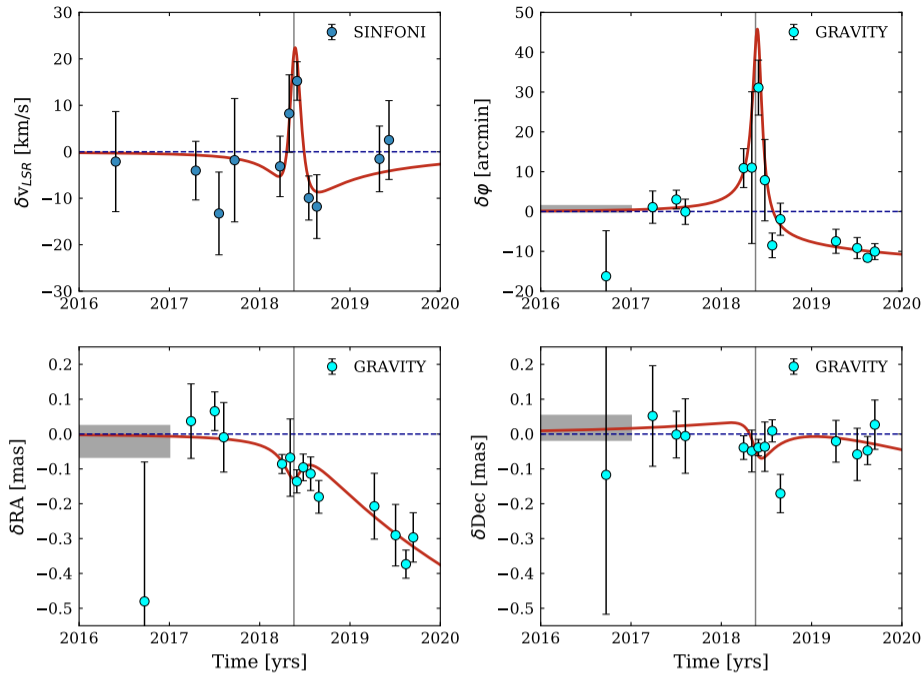
Figure 3 shows the sky-projected orbital motion and line-of-sight velocity of S2 in the past 27 years. Because of the SP, the orbit of S2 is not closed as Newtonian’s law of gravity predicted. In this work, the authors identify the SP by quantitatively analyzing the deviation of S2’s orbit from Newtonian law. A dimensionless parameter fSP , which is 0 for Newtonian orbits and 1 for GR orbits, is used to evaluate the precession.
Figure 4 illustrates how observations of S2’s orbit deviate relative to the fSP = 0 orbit (i.e. the Newtonian orbit). As we see, each panel displays a sudden kink as S2 passes through the pericenter. Assuming fSP = 1.1 (the fitting error is 0.19 and the statistical error is 0.21) fits the data pretty well, meaning S2’s orbit is not a Newtonian orbit but a GR orbit, and the kink is the effect of the SP.
Apart from the central supermassive black hole, an extended mass distribution or an intermediate-mass black hole inside the orbit of S2 can also explain its precession. The authors provide a constraint on the masses of those two possible sources, which are negligible compared to the supermassive black hole whose mass is 4.261 (± 0.012 ) × 106 Msun.
In summary, with the combined orbital motion and the superb astrometric data from GRAVITY that cover the pericenter passage period, astronomers have successfully measured the Schwarzschild precession in the orbit of S2 for the first time.