This guest post was written by Xing-Ye Zhu, a third-year undergraduate student at Nanjing University, for an assignment in the Astronomical Literature Reading and Writing class taught by Professor Zhi-Yu Zhang. Xing-Ye is currently working under the supervision of Professor Yi Xie on strong deflection gravitational lensing. When not doing science, he enjoys watching movies, plays, and Kunqu Opera. You can always find a Rubik’s cube in his hands.
Title: Relativistic corrections to the rotation curves of disk galaxies
Authors: Alexandre Deur
First author’s institution: Department of Physics, University of Virginia
Status: Open access on arXiv
For most astronomers, it is just common sense that dark matter accounts for approximately 85% of the matter in the universe. However, as long as the constituents of dark matter remain a mystery, some astronomers remain skeptical about our conventional understanding of dark matter. Recently, astronomer Alexandre Deur suggested that the theory of relativity itself may explain a phenomenon widely regarded as evidence for dark matter.
Why do we need dark matter?
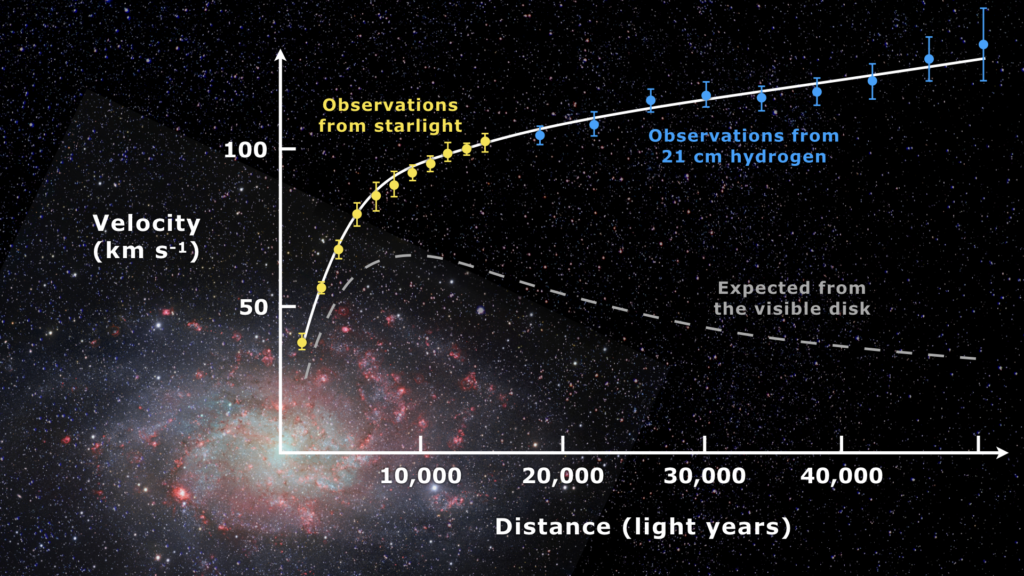
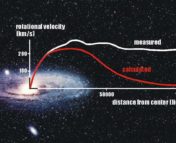
The theory of dark matter was proposed in the 1970s to explain the rotation curves of galaxies, which appeared inconsistent with the observed distribution of luminous matter (i.e. baryonic matter). The rotation curve of a disk galaxy, as shown in Figure 1, is the relation between the rotational velocity of stars in the galaxy and their radial distance from its centre. At larger radius, a typical spiral galaxy shows larger rotational velocity than the one predicted by the Newtonian gravitation of baryonic matter. The observed rotation curves typically show a plateau at large radius, therefore requiring more gravitation to keep the fast-moving stars from escaping the galaxy. This discrepancy is known as the “missing mass problem”. One possible explanation is the presence of additional mass which we cannot see. This “missing mass” is called dark matter. With the observed rotation curve, astronomers can easily calculate the missing mass required and therefore determine the distribution of dark matter.
Galaxy rotation curves are not the only evidence that exists for dark matter. For example, the Bullet Cluster is famous for being a “smoking gun” for dark matter. The Bullet Cluster consists of two merging galaxy clusters. The distribution of matter determined by X-ray imaging is very different to that inferred from gravitational lensing, suggesting the dark matter component has separated from the “normal” matter during the collision. See this website and this astrobite for further discussion. Dark matter also plays an important role in the widely accepted ΛCDM model of cosmology.
What do we think dark matter is?
For decades, astronomers have been searching for the essence of dark matter, both theoretically and experimentally. For example, astronomers have searched for WIMPs (Weakly Interacting Massive Particles) (read more in this astrobite and this one). It has also been hypothesised that dark matter may be made up of MACHOs (see this astrobite). However, the dark matter puzzle still remains unresolved, because it is challenging to completely verify or eliminate any of these theories (at least not yet). Some astronomers have suggested alternative theories. Is it possible that the “missing mass” is not actually “mass”, but an artefact arising from our mistaken understanding of the gravitation? After all, it is additional gravitation, rather than mass, that is required to explain the galaxy rotation curves.
It is not the first time physicists and astronomers have become skeptical about gravitation. One hundred years ago, the observation of Mercury’s perihelion precession was initially interpreted as evidence of another planet inside the orbit of Mercury, but was later fully explained by a new theory of gravitation: general relativity. Today, astronomers are facing a similar problem – is it something there, or is it just another correction to the theory of gravitation?
Could gravitation explain dark matter?
Modified Newtonian Dynamics, or MOND, for example, is the most discussed out of all the gravitation corrections to explain the missing mass problem (see this astrobite for further discussion of MOND vs. dark matter). It modifies the Newtonian gravitation law at low accelerations to enhance the effective gravitational attraction. Similarly, most of the other corrections require new descriptions of gravitation. But recently, as Deur proposes in this work, the effect of general relativity may account for the missing mass, without introducing any new corrections.
Generally, the predicted rotation of galaxies, as shown in Figure 1, is modelled by Newtonian dynamics. The rotation velocity is much smaller than the speed of light, especially at the outer part of the galaxy (typically , where
is the velocity and
is the speed of light). Therefore, it is believed that a non-relativistic treatment is reasonable. However, this assumption could be challenged due to the effect of field self-interaction in general relativity. This effect depends on the mass only, and is independent of the rotation velocity, thus making a difference regardless of how fast the stars move in the galaxy. Deur shows that field self-interaction, which reveals the non-linear nature of general relativity, is in fact not negligible in the missing mass problem.
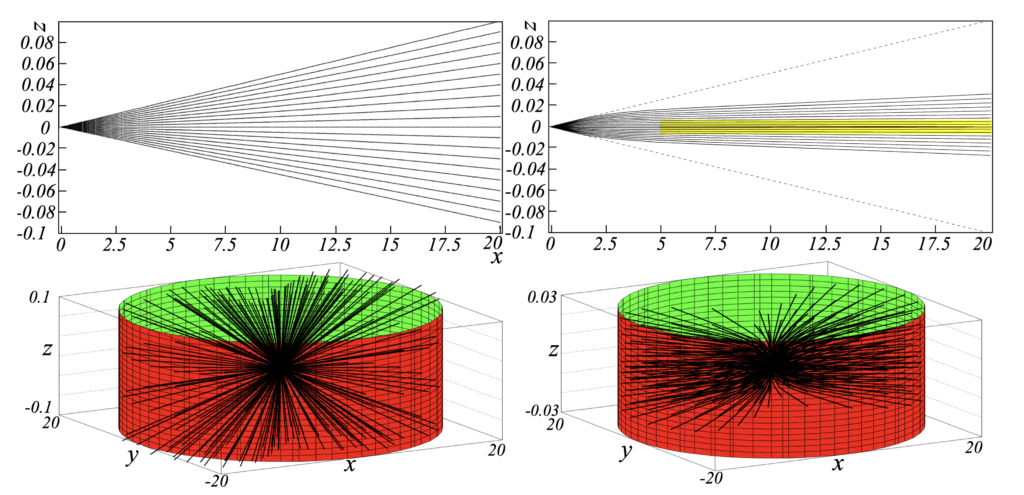
To demonstrate this, Deur uses the gravitational lensing formalism. While light travels in straight lines in flat space, it can be deflected in the presence of a gravitational field. In exactly the same way, the gravitational field lines connecting two parts of the galaxy are distorted by the background field. That is to say, the gravitational field is deformed by the total galactic mass. With the field lines distorted, the strength of the gravitation consequently changes.
In addition to this, to reduce computation, Duer uses mean-field theory, an approximation technique widely employed in many fields (ha!) in physics. In this theory, the effect of all the other particles on any given individual particle is approximated by a single averaged effect, or the “mean field”, thus reducing a many-body problem to a one-body problem. Together with the gravitational lensing formalism, the self-interaction of the gravitational fields is computed. Figure 2 shows a demonstration of this effect – it is clear that the self-interaction significantly distorts the gravitational field lines.
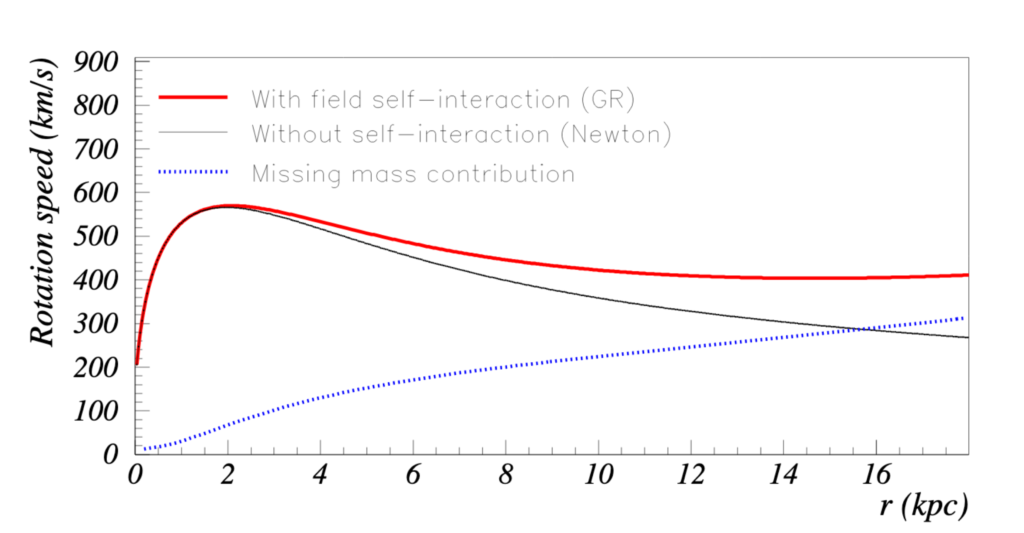
Duer demonstrates that field self-interaction increases gravity’s strength compared to the Newtonian prediction. This effect will become noticeable in systems with sufficiently large mass. In Duer’s predicted rotation curve, shown in Figure 3, the observed plateau pattern is reproduced when field self-interaction is taken into consideration. Duer also computes the effective missing mass contribution derived from the comparison between the results of general relativity and Newtonian gravitation. This comparison leads to the prediction of a correlation between galactic dark mass and the vertical scale length of the disk galaxies and the prediction fits the observational data quite well.
In summary, Alexandre Deur proposes that the effect of field self-interaction needs to be included in the computation of rotation curve of the disk galaxy. Rather than merely taking the Newtonian gravitation into account, we need to consider the role general relativity plays in the physics of the galaxy. This consideration is able to partially explain the observed galaxy rotation curve, without modelling invisible dark matter or modifying the basic theory of gravitation.
In the debate about the existence of dark matter, Deur undoubtedly proposes another interesting possibility, yet more detailed investigation is needed to verify the significance of this effect. Maybe the relativistic effect is not enough to replace the missing mass completely, for there is other evidence for dark matter to explain. For disk galaxies at least, it is still important to know how much “missing mass” we have “found”. There is still a lot of work to be done before we can say that the puzzle of dark matter is resolved. However, we are getting closer all the time!



The best evidence for the existence of dark matter comes from the cosmic microwave background and the large scale distribution of galaxies and galaxy clusters (the matter power spectrum). We do the public a great disservice by pretending that galactic rotation curves are the whole story. For those who are genuinely curious about the *best* evidence for dark matter, I refer you to this great review article https://arxiv.org/abs/1605.04909
It’s not a disservice though. By accurately predicting galaxy rotation using true nonlinear self interaction we can properly eliminate what dark mass isn’t there, to truly determine how much is there. If this more closely corresponds to other observations because we are correct then we are now ahead of the game.
I will review…Thanks for the link.
Yo creo que mas bien podria ser una teoria hibrida, de la materia oscura y una teria alternativa.
The CMB doesn’t ‘prove’ Dark Matter, only that we are receiving electromagnetic signatures, however faint, from the stars and galaxies beyond our detection, and so far away that the wavelengths have been redshifted/’stretched’ into the microwave band. So the CMB is simply a picture of the universe beyond expressed in the microwave.
I think what Gordan is referring to is the CMB power spectrum – which is a measure of how the temperature of the CMB fluctuates over different angular scales across the sky. We can model this if we have an idea of what the universe is made up of e.g. how much dark matter & dark energy & normal baryonic matter is required, as well as some other cosmological parameters. Turns out that this power spectrum when measured by Planck matches the predicted power spectrum based on the standard cosmological model extremely well! So we can use that to constrain dark matter. There’s a little tool to see how these different components affect the power spectrum here.
Like many changes to our understanding of the universe, our understanding of dark matter clearly came about through lots of different pieces of observational and theorymeasured by Planck – and the CMB power spectrum is an amazing piece of evidence that supports the standard model of cosmology. But the light curves of galaxies were also a very important observation leading to our understanding of dark matter so far!
Nicely written article, clear enough for a non-technical reader to understand. Would be happy to read more from Mr. Xing-Ye Zhu!
Thanks Gordan, that’s very useful!!
Nice article. It seems to me that for the spiral shape of a spiral galaxy to be preserved through anything like 25 revolutions one could say the galaxy is rotating as a disk. In other words there seems to be some gravitational linking between the individual stars making up the galaxy. If true then that would affect the expected velocity of the stars.
Also, I’m not sure if the low readings near the center of the galaxy are just artifacts of the instrumentation, but that seems like a bigger discrepancy than the lower than expected readings at the outer edges.
If you read the work of Professor Fred Cooperstock, which goes back to 2003, you will see that using purely a general relativity profile,instead of a first approximation, for galaxy curves, dark matter disappears. There is no need for extra maths or other alterations, simply general relativity. The work is monumental but pretty much ignored. Fred died a couple of years ago. He was professor Emertius at Victoria University in Canada and a highly regarded physicist. He published over a dozen papers on this work and also a book as well.
The book: General Relativistic Dynamics: Extending Einstein’s Legacy Throughout the Universe
https://www.goodreads.com/book/show/7240159-general-relativistic-dynamics
One of the papers: https://arxiv.org/abs/astro-ph/0507619
The barionic Tully-Fisher (BTFR) relation, M = A V^4, is well established for
spiral galaxies that have a flattend velocity curve, where M is the total baryonic
mass of the galaxy, V is velocity of the flat part of the curve, and A is a
parameter which has a fitted value A = 50 Msolar s^4 / km^4, for V in km/s and M in solar mass.
The Cooperstock paper at arxiv astro-ph/0507619 studies three NGC galaxies, among
others. For NGC 3031, he theoretically determined a mass of 10.9 x 10^10 solar
masses, whilst the BTFR, with an approximately flat velocity V = 175 km/s gives a
mass M = 4.7 x 10^10 solar masses, which is only half the theoretical value.
For NGC 3198, his value was 10.1 x 10^10 solar masses, whilst the BTFR, for an
approx. flat velocity V = 149 km/s, gives M = 2.5 x 10^10 solar masses, which is
a quarter of his value.
Finally, for NGC 7331 he determines mass 26.0 x 10^10 solar masses,
whilst the BTFR predicts, for an approx. flat velocity V = 238 km/s, gives a total
galaxy mass of 16.0 x 10^10 solar masses, which is 39 % less than his value. So,
his derivation gives too high a mass for these galaxies.
A similar assessment can also be made for the paper by A. Deur, where
his derived barionic galaxy masses are even larger in comparison to the BTFR.
I have a paper on graviton redshift which offers an explanation of dark matter and
dark energy (https://dx.doi.org/10.4236/jmp.2022.1311084).