Title: The Role of T0 in CMB anisotropy measurements
Authors: Yunfei Wen, Douglas Scott, Raelyn Sullivan and J. P. Zibin
First Author’s Institution: Department of Physics and Astronomy, University of British Columbia, Vancouver
Status: Open access on arXiv
One of the most significant observational evidence in support of the standard Big Bang model of cosmology is the existence of a (mostly) uniform background radiation permeating all space and visible in all directions. This cosmic microwave background (CMB) provides vital insights into the nature of the Universe, since measurements of its power spectrum can be used to constrain the ΛCDM cosmological model. These parameters include the density of dark matter and baryonic matter, as well as the age of the Universe. Another parameter, often overlooked, is the mean CMB temperature (a.k.a CMB monopole), denoted T0. Its value, as measured by FIRAS, of 2.7255 0.0006 K has an extraordinarily small uncertainty of 0.02%. While this uncertainty has so far been small enough to neglect, future large-scale structure surveys (such as Euclid) will probe the CMB power spectrum to within a much finer precision. The authors of this paper consider whether T0 can continue to be treated as a constant, or if a more precise value is needed in order to better constrain ΛCDM.
Poles apart
The CMB is not completely uniform, instead featuring many anisotropies that can collectively be described by a power spectrum (not to be confused with its thermal, blackbody spectrum). A large amount of data reduction is required to go from raw CMB data (such as that measured by COBE) to a CMB power spectrum and, ultimately, parameters for ΛCDM. One step along the way involves decomposing the data into spherical harmonics. The letter l is used to denote the degree (or order) of the spherical harmonic. We say that l = 0 corresponds to the monopole expansion, l = 1 the dipole expansion, l = 2 quadrupole, l = 3 octupole and so on. Larger values of l correspond to smaller spatial scales. It turns out that the current measurement of T0 is so precise that it only starts to affect calibrations past the l = 1000 pole.
Seventh sanctum
Usually, T0 is used as a fixed calibration temperature to convert the (dimensionless) CMB spectrum into units of temperature. Should the value of T0 change in the future, current results would have to be recalibrated. The authors consider deploying T0 in a much more central role, as a 7th cosmological parameter (in addition to the standard 6 from ΛCDM) that is used to set the timescale and allowed to change over time. T0 traces the overall amount of radiation in the Universe, and so it is possible to model the density of baryonic matter and dark matter as functions of this cosmic temperature alone. Current observations of CMB anisotropies provide weak constraints on T0, based on CMB lensing and the integrated Sachs-Wolfe effect. In particular, there is the well known degeneracy with Hubble’s constant T0. Figure 1 shows the H0-T0 plane, coloured according to the dark energy density parameter, as sampled from the 2018 Planck data using the new ΛCDM+T0 7-parameter model.
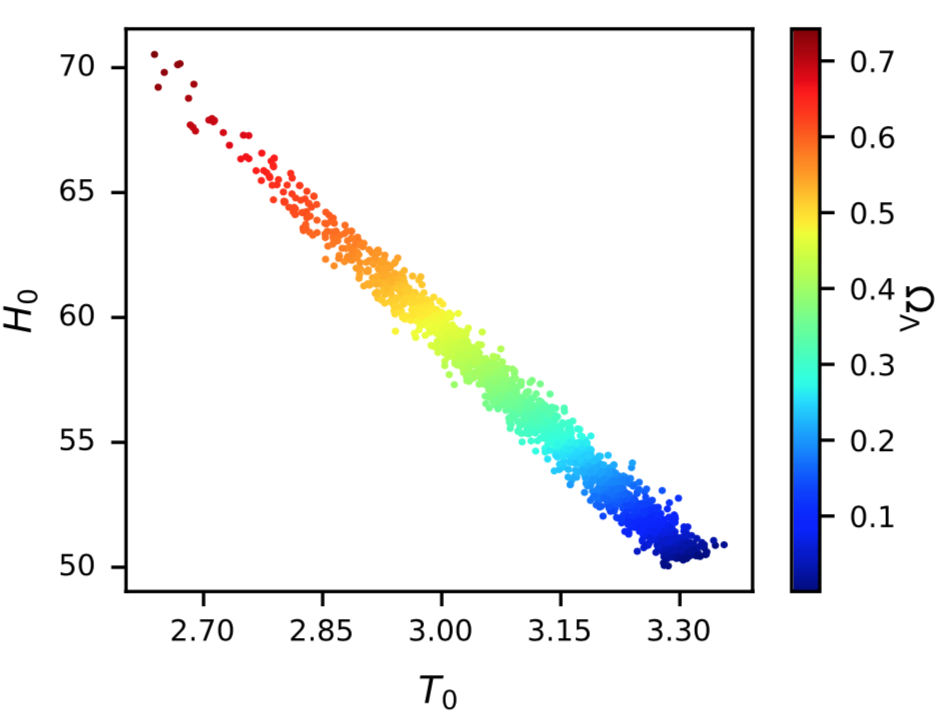
As an aside, this close link between T0 and H0 is often touched upon in the context of the Hubble tension (the mismatch in the value of H0 as implied by the CMB and that derived from distance-ladder observations). Astrobites has covered this topic extensively in many previous posts. The authors of this paper explicitly comment on how changing the value of T0 does not resolve the Hubble tension, nor will it resolve tensions with other cosmological parameters.
A non-negligible effect
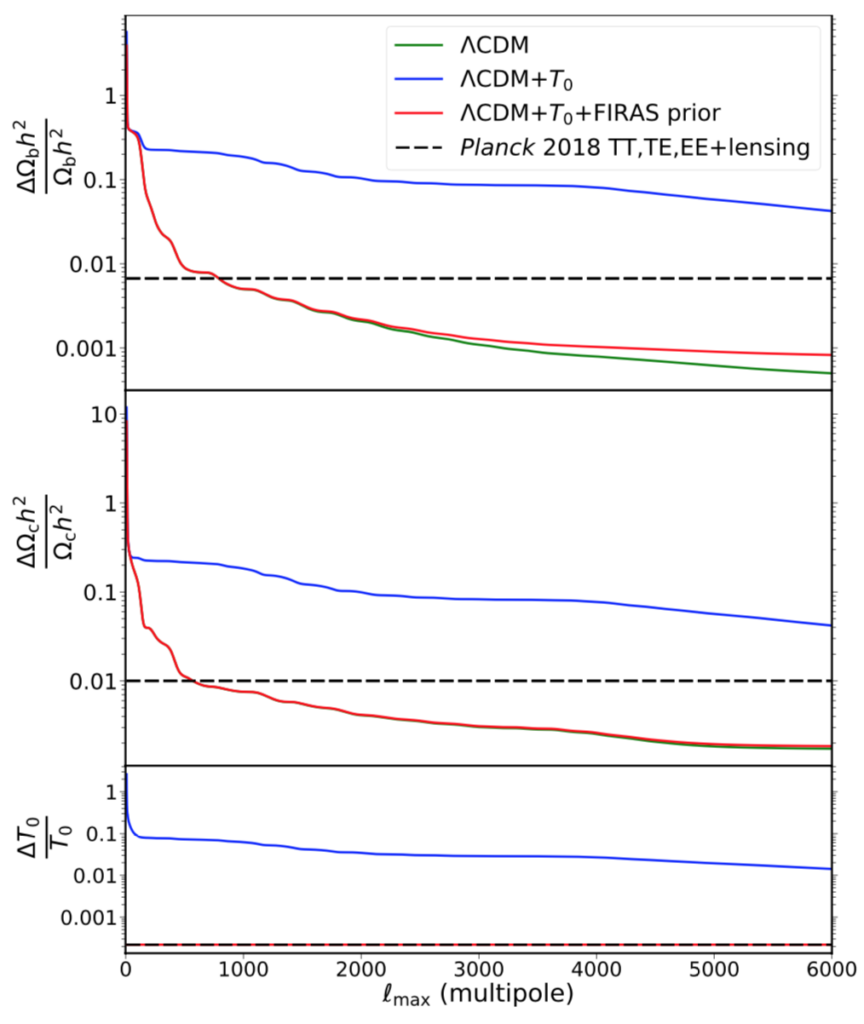
To see how the 7-parameter ΛCDM+T0 (with the FIRAS value of T0) compares to the standard 6-parameter ΛCDM, the authors consider its effects on the physical baryon and dark matter density parameters. Using a Fischer matrix analysis (the bane of every statistics class), the authors found that there is little difference in the overall baryon density error up until multipole 2000, where the uncertainty of the FIRAS measurement (relative error around 10-3) begins to manifest, and further deviates right through to multipole 6000 (compare the red and green plots in the top panel of Figure 2). There is a similar albeit less dramatic deviation for the dark matter density; this is since the baryon density is more strongly constrained by higher-multipole CMB spectra. Figure 2 shows that the FIRAS uncertainty will have non-negligible effects on the constraints of ΛCDM parameters at very high multipoles. The authors note that the current FIRAS value is more than suitable for current CMB surveys, and will remain suitable until such time when future surveys are able to probe beyond the cosmic variance limit out to multipoles of the order of thousands.
Some fine tuning to keep in mind
In addition to looking at the role of T0 as a seventh ΛCDM parameter, the authors also strongly advocate for the use of dimensionless units (e.g. ΔT/T) to analyse the CMB spectrum. Given that the CMB anisotropies are by nature dimensionless, T0 is simply applied as a means of unit conversion into the conventional units of Kelvin.
As it currently stands, the FIRAS uncertainty is so small that it has virtually no impact on current observations and structure surveys. However, as the capabilities of future surveys will undoubtedly improve, there will eventually be a need to seek out a more accurate value of T0. Only then will it be possible to fully extract and constrain the CMB spectra measured to l = 5000 and beyond, ultimately fine tuning our understanding of how the Universe has and will continue to evolve.
Featured image credit: NASA (WMAP)
Edited by: Jason Hinkle
The author wishes to acknowledge the Whadjuk peoples of the Noongar nation, the traditional custodians of the land on which this post was written, and pays respect to Elders past and present.