Title: Consistent equivalence principle tests with fast radio bursts
Authors: Robert Reischke, Steffen Hagstotz, Robert Lilow
First author institution: Ruhr University Bochum, Faculty of Physics and Astronomy, Astronomical Institute (AIRUB)
Status: available on arXiv
How can we test an extremely successful scientific theory using an object we know very little about? That’s a fascinating question and precisely what the authors of today’s article aim to do. The target theory: Einstein’s general relativity. The tool: fast radio bursts.
General relativity (GR), first put forth in 1915, remains the best theory of gravity and is currently the bedrock for modern astrophysics and cosmology. It has been experimentally verified in a multitude of cases, as it explains the strange orbit of Mercury, the bending of light by massive objects, tiny time delays in GPS systems, and most recently the detection of ripples through spacetime itself. Despite these successes, GR cannot be the final theory of gravity, as it doesn’t play nicely with other fundamental forces, so stress-testing the theory and looking for tiny deviations might give us a hint into what an ultimate theory could look like.
Fast radio bursts, in contrast, are a much more recent discovery. The first confirmed FRB was reported in 2007 (you can look at a list of all currently announced FRBs here). Most FRBs are one-off events, with only a few repeating. While the source of FRBs is unknown (though there are some ideas), for the purposes of today’s study, there are only two key properties that are needed to test GR:
- FRBs are very very bright—bright enough that we can see them across cosmic distances.
- They are short lived, transient events (hence the fast in their name). FRBs typically only last a few milliseconds.
To understand how we can test the limits of GR using FRBs, we need to understand two key ingredients: dispersion measures and the equivalence principle.
Dispersion measures
If GR holds, then the speed of light in a vacuum is 299792458 m/s, for all observers, for all types of light. However, when light travels through a material, the speed of light changes, sometimes dramatically (the speed of light in glass is about 2/3 of the speed of light in vacuum). However, more importantly, when light travels through a material, not all colours of light travel at the same speed anymore. This effect, where different wavelengths of light travel at different speeds through a material, is called dispersion, and explains why a glass prism splits white light (all colours travelling together) into different coloured rays (the different speeds mean the light travels at a different angle through the glass).
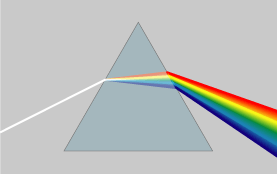
Attribution: CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=57730
In astrophysics, the amount of dispersion depends on how many free electrons there are along the light’s path, as light interacts with these charged particles and various wavelengths interact differently. This means that a short pulse of electromagnetic radiation released by a source (like an FRB) containing both high energy and low energy photons ends up being smeared out when we receive it. We see the high energy photons first, as they breeze past the charged particles mostly uninterrupted, while the low energy photons are more delayed. This means that a single, very short pulse at the source looks to us like a broader pulse that happens over some amount of time.
By measuring the delay between when we receive the first, high energy photons and when we receive the last, lower energy photons, we can build a metric called the dispersion measure of the source. This tells us about how many electrons there are between the source and us. Therefore, if we have a model from other sources about the distribution of electrons in the universe, we can turn this dispersion measure into a measurement of distance.When we examine FRBs, their dispersion measures are far too high for the source to be within our galaxy. So while we don’t know what causes FRBs, we do know that they are extra-galactic and their light travels over very large cosmic distances, which means they must be intensely bright.
The fact that FRBs are so far away turns out to be very important for this study, as it means that their dispersion measures are dominated by the electrons between galaxies. That means they are expected to trace the large scale structure of the universe, though potentially with some bias.
The Equivalence Principle
There are many different ways that you can look for deviations from GR. Given a particular model of modified gravity, you can look for signatures of that specific theory. However, this paper tries to look at deviations from GR without assuming a specific alternative. They do this by using the Parametrised Post-Newtonian formalism, which defines several numbers that characterise different ways observations can deviate from GR. For the purposes of this paper, the test is of how well the equivalence principle (EP) holds.
In particular, the EP predicts that in a vacuum, light of all wavelengths should travel along the same path at the same speed. The parameter used to characterise whether the EP holds for light is called Δγ, which takes the value 0 if GR, and therefore the EP, holds. So, if Δγ is actually some value different from 0, light of different frequencies travels at different speeds even in vacuum. That means a short pulse of many different wavelengths gets smeared out into a broader pulse, in much the same way travelling through a medium does with dispersion. It is this additional source of time delay that today’s authors want to nail down.
Putting it all together
Now what good does this do for us? If we just have a measurement from a single FRB, there is no way to disentangle these two different sources of time delay. It could be that the EP isn’t violated and the extra time delay comes from the FRB being further away, OR it could be that the FRB is closer and therefore has less dispersion, but the EP is violated so there is an additional delay.
This is where the main point of the paper comes in. If you have a set of FRB signals and measured time delays, we can look at the statistics of how those time delays are distributed across the sky and hope to disentangle the competing effects that way. The particular statistic used to extract this information is the power spectrum, which is closely related to the 2 point correlation function.
We have many measurements of how matter is distributed on large scales. With a particular bias model, this extends to the distribution of electrons in the universe and thereby to the statistics of dispersion measures from FRBs.
Today’s paper shows that the different sources of time delay: EP violation and dispersion, have characteristically different shapes in their statistics. This boils down to the fact that the correlation functions for the matter distribution (which dictate the dispersion measure) have a different shape than the correlations for the gravitational potential (which sets the time delay from EP violations). For those of you who want the details in the equations, compare the forms of equations 24 and 25 in today’s paper.
If the measured power spectrum of dispersion lacks the characteristic EP violating shape, this non-detection places very strong bounds on how much the EP can be violated. With a mock catalogue of 1000 FRBs, the authors demonstrate that a non-detection of this specific signal places tighter constraints on Δγ than previous methods. As the number of observed FRBs grows, so does the sensitivity to this effect, and subsequent detections or non-detections could prove to be a good probe of testing general relativity on cosmological length scales. Currently about 500 FRBs are known and confirmed, but current and future experiments are raising that number quickly, so watch this space for exciting new applications of these mysterious objects!
Astrobite edited by Ashley Piccone
Featured image credit: Dark Side of the Moon album cover, licensed by fair use from Wikipedia. Photo of Albert Einstein: MPI/Getty Images