Title: Universality of free fall from the orbital motion of a pulsar in a stellar triple system
Authors: Anne M. Archibald, Nina V. Gusinskaia, Jason W. T. Hessels, Adam T. Deller, David L. Kaplan, Duncan R. Lorimer, Ryan S. Lynch, Scott M. Ransom, and Ingrid H. Stairs
First Author’s Institution: Anton Pannekoek Institute for Astronomy, University of Amsterdam and The Netherlands Institute for Radio Astronomy (ASTRON)
Status: Published in Nature; open access on arXiv
Albert Einstein’s Equivalence Principle
One of the guiding ideas that led Einstein to develop the general theory of relativity (GR) was Einstein’s equivalence principle (EEP), which asserts that the gravitational and inertial masses of an object must be the same. Thus, it is not possible to physically distinguish between the inertial forces resulting from accelerating through space (e.g., in a rocket ship) and the force of gravity due to the curvature of space-time (e.g., near the surface of the Earth). The EEP therefore requires that objects in an external gravitational field fall identically, also known as the universality of free fall. An extension of the EEP is the strong equivalence principle (SEP), which states that the universality of free fall should also apply to self-gravitating bodies such as neutron stars. Tests of the SEP are important for constraining the nonlinearity of gravity, and there are very few theories of gravity, other than GR, that satisfy the SEP.
PSR J0337+1715: A Hierarchical Stellar Triple System
PSR J0337+1715 is the first millisecond pulsar (MSP) stellar triple system to be discovered out of more than 300 known MSPs in the Galaxy and globular clusters. The pulsar is in a 1.6 day orbit with a white dwarf weighing ~0.2 times the mass of our Sun, which are both also in a 327 day orbit with a ~0.4 solar mass white dwarf (see animation). Surprisingly, the orbits are nearly circular and coplanar, which suggests that this particular stellar triple system experienced an exotic and complex evolutionary history that differs from other stellar systems. Since the gravitational field of the outer binary strongly accelerates the inner binary containing the pulsar (which has strong self-gravity), PSR J0337+1715 offers an ideal laboratory for performing strong-field tests of the SEP.
Testing the Strong Equivalence Principle
In today’s astrobite, we cover a new test of the SEP based on radio pulsar timing measurements of PSR J0337+1715. The authors observed the pulsar at radio frequencies between 1,100 and 1,900 MHz for more than 1,200 hours, spanning approximately six years, using the Westerbork Synthesis Radio Telescope (WSRT), the Robert C. Byrd Green Bank Telescope (GBT), and the William E. Gordon telescope at the Arecibo Observatory (AO). Precision pulsar timing techniques were used to measure pulse times of arrival (ToAs) from the MSP. This involves folding short observations of the pulsar modulo its rotational period using a model that also accounts for its orbital motion. Since a full model of the system’s complex three-body interactions was too complicated to use for real-time observing, the authors carried out short 10 second integrations of the pulsar and folded the data using a modified two-Keplerian-orbit model. The recorded profiles were then phase-shifted to match the predictions from the full three-body model. These 10 second phase-corrected observations were averaged together to form longer ~20 minute integrations, which were compared to a standard template (see Figure 1) to derive ToAs from the pulsar.
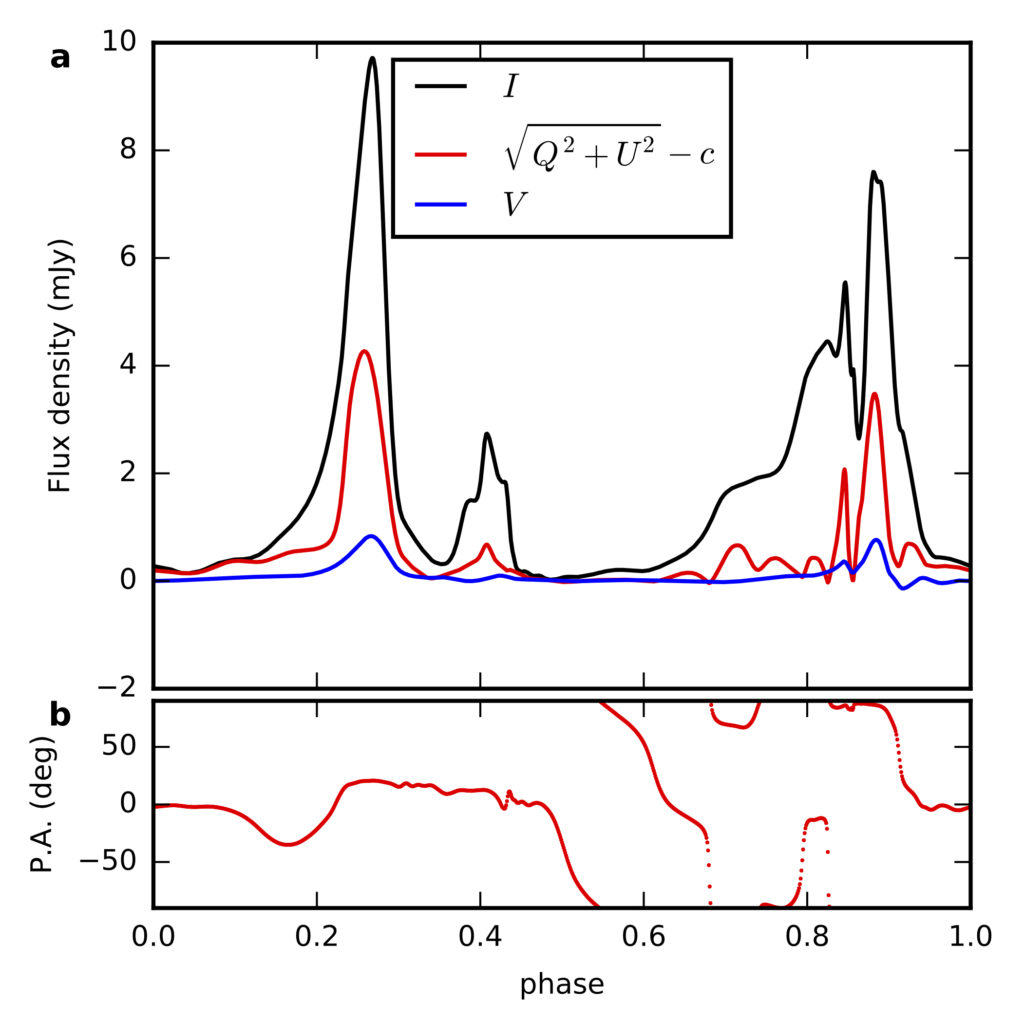
Figure 1: Template pulse profile used to measure pulse times of arrival (ToAs) from PSR J0337+1715. (a) Stokes IQUV profiles (I: total intensity; Q, U: linear polarization; and V: circular polarization) after correcting for Faraday rotation and subtracting an offset, c. (b) Polarization angle (P.A.) at the center frequency of the observation. The profile has a complex polarization structure, and the linear polarization (red) is responsible for nearly 50% of the flux density at some phases. Credit: Extended Data Figure 1 from the paper.
Using roughly 27,000 ToAs (see animation), the authors were able to constrain the SEP violation parameter (Δ), a measurement of the fractional difference between the inertial and gravitational masses of the pulsar. They found that the inner white dwarf and the pulsar experience accelerations that differ by no more than |Δ| < 2.6 x 10-6 (95% confidence, including systematics), which is nearly a thousand times smaller than constraints from other strong-field tests.
Since the SEP is only satisfied when Δ = 0, the authors searched for signatures of a non-zero value of Δ in their timing residuals (see Figure 2). The authors show that a non-zero Δ would introduce a sinusoidal signature into the residuals with a frequency of 2f inner – fouter, where f inner and fouter are the inner and outer orbital frequencies. This effect would be produced by differential acceleration in the system, which would shift the inner orbit of the pulsar toward the outer white dwarf. However, the authors argue that they would have detected a signature of Δ = 2.6 x 10-6 (shown in Figure 2c) in Figure 2b if a SEP violation of this magnitude was present in the data. Since this structure is not observed, there is not significant evidence to suggest that there is a violation of the SEP.
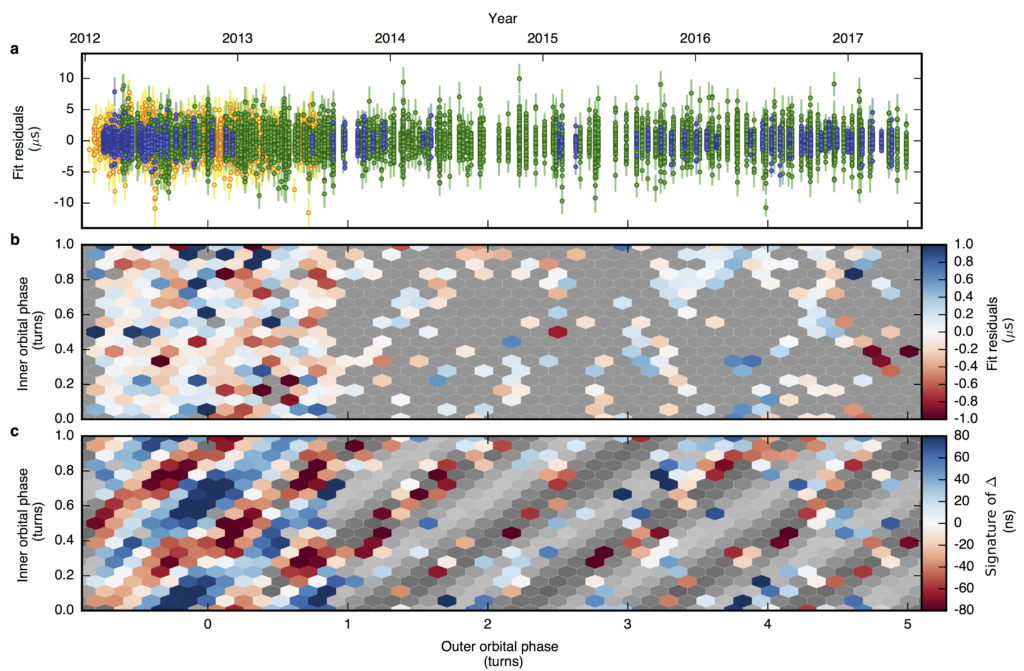
Figure 2: Difference between pulse arrival time measurements and the timing model. (a) Residuals from the WSRT (orange), GBT (green), and AO (blue) data. The error bars correspond to 1σ statistical uncertainties derived from the template matching procedure. (b) Values from (a) binned by the inner and outer orbital phases to reveal structure that varies with the inner orbital phase. (c) SEP violation signature of Δ = 2.6 x 10-6. The axes in (b) and (c) show the fractional number of revolutions of each corresponding orbit. Note the different scales of the residuals in (b) and (c). Credit: Figure 1 from the paper.
Did Einstein Get It Right?
Tests of the SEP involving neutron stars are particularly valuable because the curvature of space-time inside a neutron star is among the largest accessible to observation. SEP violations are predicted at some level from most metric theories of gravity, other than GR, and PSR J0337+1715 has provided us with a new and important test of gravity. In the weak-field regime, lunar laser ranging has placed a limit of |Δ| < 1.3 x 10-14 (95% confidence) using the Earth-Moon-Sun system by measuring the round-trip light travel time of laser pulses transmitted from the Earth to the Moon and reflected back to Earth. More precise measurements will allow for increasingly stringent tests of gravity. At the moment, Einstein’s general theory of relativity remains compatible with the best tests of gravity performed thus far. However, a debate is now emerging regarding whether or not additional measurements may be needed to show the equivalence holds at the smallest length scales.