Title: Robust marginalization of baryonic effects for cosmological inference at the field level
Authors: Francisco Villaescusa-Navarro, Shy Genel, Daniel Anglés-Alcázar, David N. Spergel, Yin Li, Benjamin Wandelt, Leander Thiele, Andrina Nicola, Jose Manuel Zorrilla Matilla, Helen Shao, Sultan Hassan, Desika Narayanan, Romeel Dave, Mark Vogelsberger
First Author’s Institution: Department of Astrophysical Sciences, Princeton University, Peyton Hall, Princeton NJ 08544, USA
Status: Preprint on arXiv
At one time or another, I’m sure we’ve all asked ourselves during a lecture, “Will I ever use this in real life?” Surely, this is a question worth considering, but often it is replaced by a more urgent question – “Will this be on the test?”
Today’s paper takes this classic internal dialogue and adds a twist – the student is not a person like you or me, but rather a machine learning algorithm (a Convolutional Neural Network [CNN]) trained on cosmological simulations. The authors want to allow the CNN to study some simulations and then present it with a question of a kind it has never seen before on a test. If it gets the question right, this is an indication of robustness of the model. We’ll unpack why robustness is something we want in a cosmological model in today’s bite!
The sky’s the limit
How much cosmological information is out there in the sky? If we could model the whole sky at once, we might be able to make progress on this question. This is the idea behind “field-level inference” – we want to take a (2D) map of the sky and directly compare it pixel-by-pixel with a model that assigns values to these pixels. This method potentially accesses more physical information than the usual “summary statistics” used in cosmology that are computed from sky maps (i.e. the power spectrum or correlation function).
One way to generate a model for these maps is with simulations – but running a simulation for every choice of cosmological parameters isn’t computationally feasible – especially for simulations that employ detailed hydrodynamic physics (like those in today’s paper). A way out of this problem is to introduce the concept of “surrogate models” that approximate the simulated (physical) models at a fraction of the total cost after they are trained. One such example of surrogate models is neural networks. Neural networks are trained on some input set of simulations and are tested on how well they have learned the material by presenting them with unseen data.
Being one-time students, we all are very familiar with this idea. We are also familiar with the idea that questions very similar to the homework that show up on the test are easy when compared to questions that ask about the material in a way we haven’t seen before. But if we can answer the latter type of question, it is a sign we are on the way to mastering the material.
This roughly corresponds to the idea of robust modeling – if a neural network is presented with unseen “test data” that is generated from a simulation with different overall physics, but is encoding the same cosmological physics, it would be ideal if the network could find the correct answer (the cosmological physics) in this unfamiliar way of asking the question.
Robustness is highly desirable in a cosmological model because cosmologists are uncertain about what happens physically on small scales, particularly due to “baryonic effects” like feedback from supernovae and Active Galactic Nuclei. This is exactly the idea behind today’s paper – but to do this training requires a lot of simulations!
Figure 1: Maps of projected total mass from two sub-models of the CAMELS simulations – IllustrisTNG (top) and SIMBA (bottom). The box side length is 25 Mpc/h. Figure 1 of today’s paper.
Study time – saddling up some CAMELS
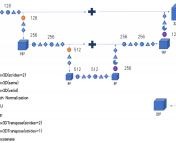
The training and test data used in today’s paper comes from the CAMELS suite of simulations – cosmological simulations including the effects of hydrodynamics and astrophysical processes. In particular, the CAMELS simulations include two astrophysical modeling choices – using the model of the IllustrisTNG simulations or the model of the SIMBA simulations. In particular, the authors generate an astronomical 30,000 2D maps of the projected total mass from the CAMELS simulations for training and testing the neural network (NN) model (see Figure 1). The way the authors test for robustness is to train a neural network model on maps generated from one class of simulations (e.g. IllustrisTNG) and then test the model by trying to infer the value of some cosmological parameters from a map generated from the other (e.g. SIMBA). The authors know the answer in advance, so the idea is that one should be confident in the model if it gets the right answer on the unseen simulation maps – i.e. the model is robust.
Figure 2 directly gets at this idea – here the NN model attempts to learn the cosmological parameter describing the matter overdensity, Ωm. The figure shows that with a few percent scatter, they find that this is usually the case. Of particular interest are the blue and green points, which are the “unseen” tests that are meant to demonstrate robustness of the model. The accuracy on the unseen test simulation is comparable to the accuracy of the same simulation, which seems to indicate that the model is learning the common cosmological physics in a way that is mostly robust to the choice of astrophysical modeling.
Figure 2: The difference in the NN-predicted and true values of cosmological parameters on the test set of simulated mass maps. The horizontal axis shows different values of the matter overdensity parameter Ωm used for testing. Blue points show predictions of the model trained on SIMBA and tested on TNG (green points show the converse), while red and purple show the predictions of the model when tested on maps generated from simulations with the same underlying astrophysical models – red for TNG and purple for SIMBA. Adapted from Figure 2 of today’s paper.
A lesson of today’s paper is that using machine learning to directly model the map has the potential to be a powerful method of constraining cosmological parameters from large-scale structure. Crucially, the authors argue that the test performed in the paper demonstrates that their NN model is robust to changes in astrophysical modeling. While the projected mass maps used in today’s paper are not actually observable, the method as outlined here may be applied to related quantities in the context of weak lensing observations in the future.
Edited by: Graham Doskoch
Featured Image: CAMELS team


This is the idea behind “field-level inference” – we want to take a (2D) map of the sky and directly compare it pixel-by-pixel with a model that assigns values to these pixels.
would the robustness of a 2d model work in a 3d field
would the robustness of a 2d model work in a 4d field
by what level of pixelation would you be out in a 2d model = zero %
in a 3d model = 75%
in a 4d model = 5% compared with the factual out there