Title: Accurate modeling of grazing transits using umbrella sampling
Authors: G. J. Gilbert
First Author’s Institution: Department of Astronomy and Astrophysics, University of Chicago, Chicago, Illinois
Status: Accepted for publication in AJ, pre-print available on the arxiv
Today’s author is using umbrellas to accurately model the planets that “graze” their stellar hosts.
Planets that Graze on their Stars
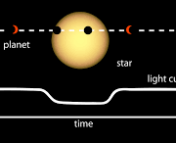
Roughly 75% of all known exoplanets were discovered via transit surveys. These are surveys that monitor the brightnesses of many stars at once, looking for dips in these brightnesses. These dips could be caused by a planet passing, or “transiting,” in front of the star. Although rare, some of these planets only “graze” their host stars, meaning that they only partially transit their parent star’s disk (check out this astrobite to learn more about a specific case of a grazing planet).
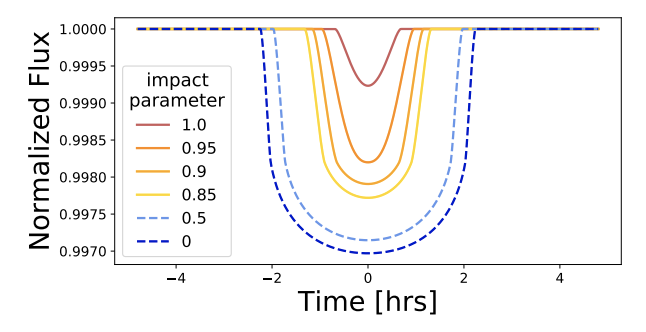
In astronomical terms, “grazing” planets are defined as those that have an impact parameter that is larger than the ratio of the planet’s radius to the star’s radius. The impact parameter is defined as the distance between the center of the stellar disk and the center of the planetary disk at conjunction, where conjunction is the point in a planet’s orbit where it is most closely aligned with its star, as viewed from Earth. An impact parameter of 0 is a case of a perfectly-centered transit, and an impact parameter of 1 is a case where only half of the planetary disk transits in front of the stellar disk.
Figure 1 demonstrates how the shape of the light curve from a transiting planet changes as a function of impact parameter. The depth of the dip in a light curve allows astronomers to estimate the planet’s radius relative to the star, but if the planet is grazing, then this estimation becomes more difficult. For example, the light curve of a smaller, non-grazing planet could look the same as the light curve from a larger, grazing planet. One therefore needs to simulate grazing transits even in cases where it is unlikely that the planet grazes its host star.
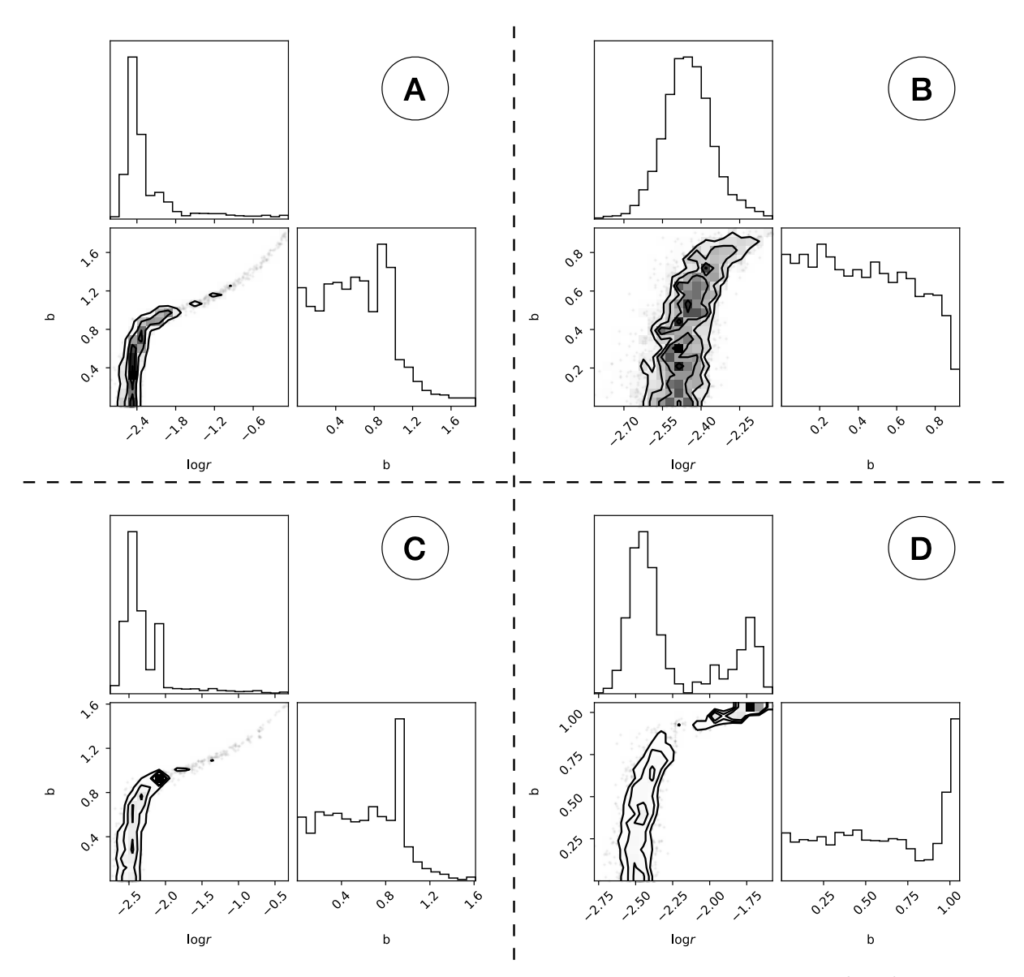
However, today’s author shows that standard Monte Carlo methods, which are frequently used by exoplanet scientists to model grazing planets, can lead to unreliable results! Identical runs of the same model can return differing results, or results where it is not obvious that the model is wrong (Figure 2)! When dealing with a handful of planets, one can let the simulation run for a longer period of time, or add additional data, such as the spectrum of the star, to the model. However, for larger samples, a more efficient method is needed. So what can astronomers do instead?
Umbrella-ella-ella
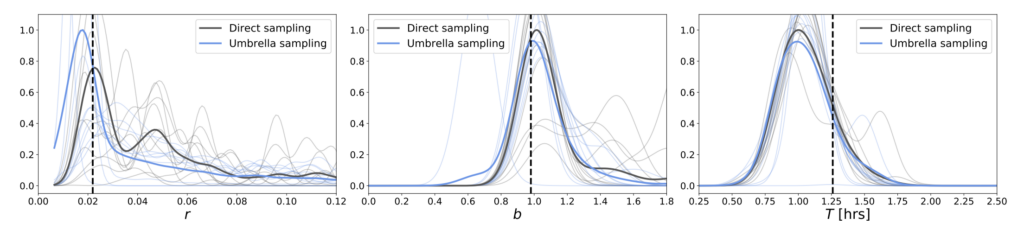
They can use umbrella sampling! Umbrella sampling is a technique that has been used in other scientific fields for decades, but not by astronomers until recently (specifically, Matthews et al. (2018) was the first to introduce umbrella sampling to the field of astronomy). One uses this technique by splitting a distribution into sub-regions, sampling from each of these sub-regions independently, and recombining these samples into a single posterior distribution (Figure 3). The author finds that this technique returns more reliable results than those from standard Monte Carlo methods (Figure 4)!
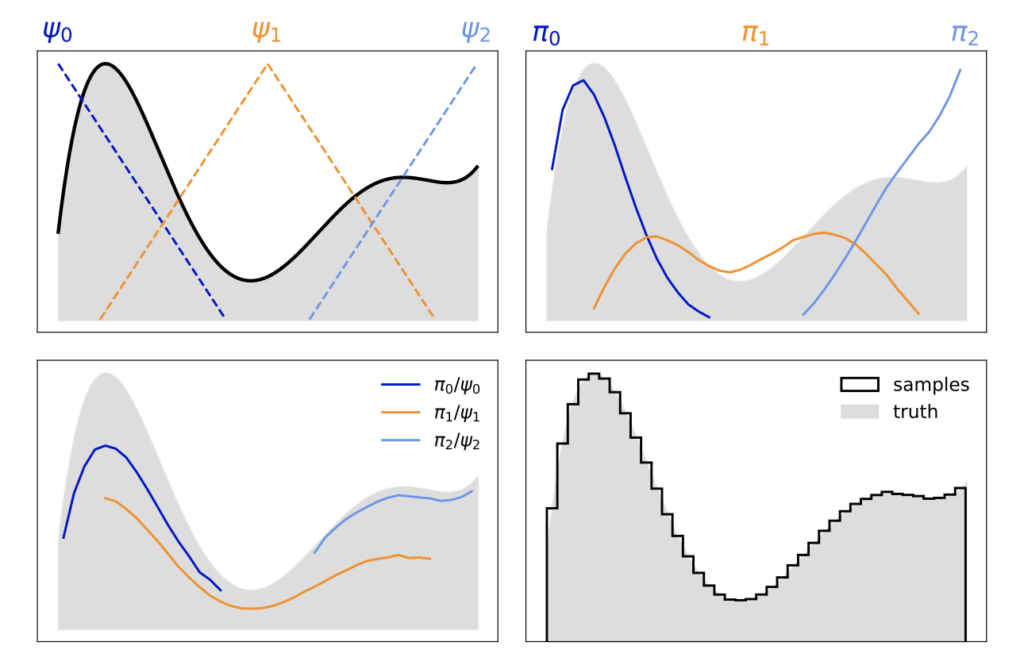
A good deal of math is needed to properly weight the sub-regions relative to one another; these calculations are described in detail in the paper, and a step-by-step tutorial can be found on the author’s GitHub. Nonetheless, the math is worth it, as this technique can be used to explore any complicated distribution, so it can be used in fields beyond exoplanet science. This means you should get out your umbrellas, ‘cause it’s gonna be raining grazing planets!
Astrobite edited by Jana Steuer
Featured image credit: G. J. Gilbert