Title: Exploring Supernova Gravitational Waves with Machine Learning
Authors: Ayan Mitra, Bekdaulet Shukirgaliyev, Y. Sultan Abylkairov, Ernazar Abdikamalov
Status: Submitted to MNRAS. [open access]
First Author’s Institution: Department of Physics, Nazarbayev University, 53 Kabanbay Batyr Ave, 010000 Astana, Kazakhstan
How does one measure the gravitational wave signal of a supernova if each event is unique? The authors of today’s paper use machine learning to classify the progenitors of over 400 supernova waveforms and determine what qualities, if any, best predict the original mass of the star that died.
Beauty Has Been Skin Deep
When a supernova (SN) occurs, the center of a dying star warps the very fabric of space and time around it, generating ripples that we measure as gravitational waves (GWs). The deaths of massive stars can result in black holes (BH) and neutron stars (NS), the behemoth corpses of our cosmos. Yet, astronomers are unable to look directly at them as they form— the innermost region of the star is so dense that it takes hours for photons to escape. During those few hours, the photons ricochet inside the star, gaining and losing energy, such that they no longer carry information about the environment where they were born.
Conversely, astronomers can immediately observe the formation of a NS or BH through gravitational waves, the imprint their motions leave on spacetime. Multimessenger observations of supernovae will be incredibly valuable for this insight. However, compared to the familiar binary in-spirals of black holes, SN GWs are a bit more complicated, producing waveforms that are unique per event and difficult to interpret intuitively.
These hurdles currently prohibit astronomers from learning the details of the innermost parts of a newborn corpse star, such as how the neutron star equation of state behaves or at what moment it actually becomes a black hole. Surprisingly, astronomers also do not know which stars (called “progenitors” by SN astronomers) become which stellar corpses when they die. Today’s authors sought to extract the progenitor mass of a SN by applying a machine learning algorithm to its gravitational wave signature and probe which moments of the gravitational wave signal best encode this information.
It’s What’s Inside That Counts
In its final hours, a star’s core fuses all the elements in the periodic table from hydrogen to iron. Meanwhile, the rest of the star’s layers feel drawn to the center by gravity. As these outer layers are dragged down, the core material acts as a hardened surface, rejecting in-falling material and “bounces” it back up (Figure 1).
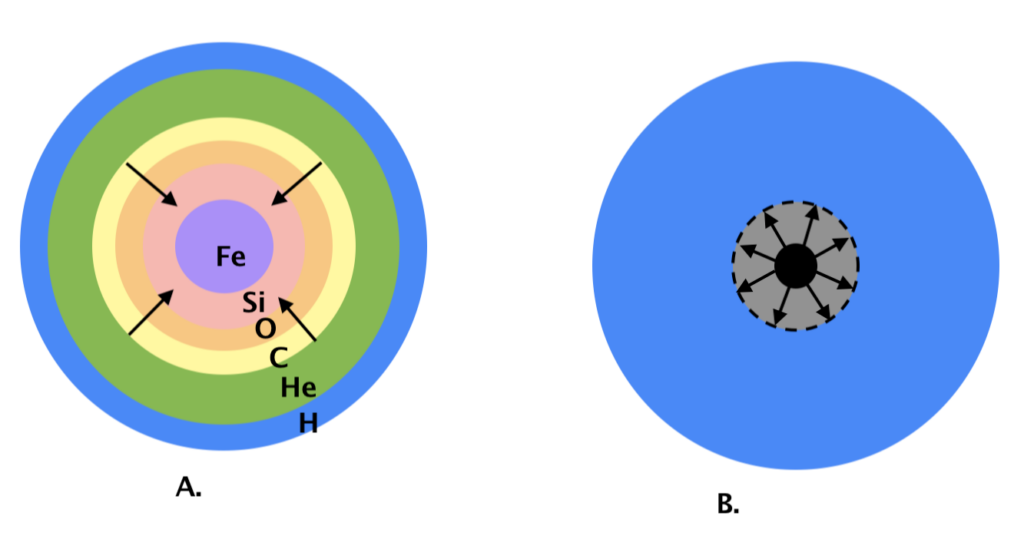
The material bounces off the surface and a shock wave (dashed line) forms. If the shock is strong enough to survive to the surface of the star, it will unbind it completely and explode as a supernova.
But there is another factor: how a star spins. Some stars rotate slowly, and others so rapidly that they flatten to an egg shape (such as Achernar for example). The centrifugal force generated by strong rotation can also contribute greatly to the net direction of force and pressure within a dying star. Thus, rapidly rotating models avoid implosion via the magneto-rotational mechanism: the kinetic energy from their rotation sources the explosion. The proto-neutron star at the center of the explosion becomes slightly more egg-shaped as it rotates, creating a perturbation viewable with GWs. The more massive the object or more aspherical it is, the greater the GW strain (or “strength”) to be measured on Earth.
In non-rotating or slowly rotating stars, neutrinos emitted from the surface of the core (or proto-neutron star), cannot escape and cause a flurry of convection. There is a stand-off between the material that wants to rain down and the neutrino pressure trying to escape, called “SASI” (Standing Accretion Shock Instability). When that outward pressure wins, the explosion occurs and prevents the star from completely falling in on itself.
Therefore, the dynamics of the densest regions of the supernova depend strongly on the strength of the star’s rotation, and in turn, so do the gravitational waves. The GW signatures of the rapidly rotating models are most affected by their oblateness, while the non-rotating models are thought to be most affected by the core bounce.
The Wisdom of Machine Learning
The authors of today’s paper applied a machine learning (ML) technique called a “random forest” to numerically-generate supernova gravitational waves. A random forest works much like a flowchart’s logic, representing a large number of decision trees (explained in this AstroBite!). The authors generated the waveforms from a host of different starting conditions (Figure 2).
The following characteristics were sampled by the authors in the generation of their SN waveforms:
- 100 different rotational profiles, ranging from slow to fast.
- Deleptonization: how much of the core mass is radiated away in leptons — electrons and neutrinos. (This affects the energy budget and the core mass by +/-10%)
- 4 different Zero-Age Main-Sequence (ZAMS) progenitor masses: 12, 15, 27, and 40 solar masses. (These are sizes commonly used in the literature.)
Through each of these combinations, the authors found 402 total SN models successfully exploded (as opposed to collapsing in on themselves). The next step was to train a fraction of their waveform bank on the ML algorithm to see if it could correctly identify the ZAMS mass of the remaining, untested population.
The Beauty in The Eye of the Classifier
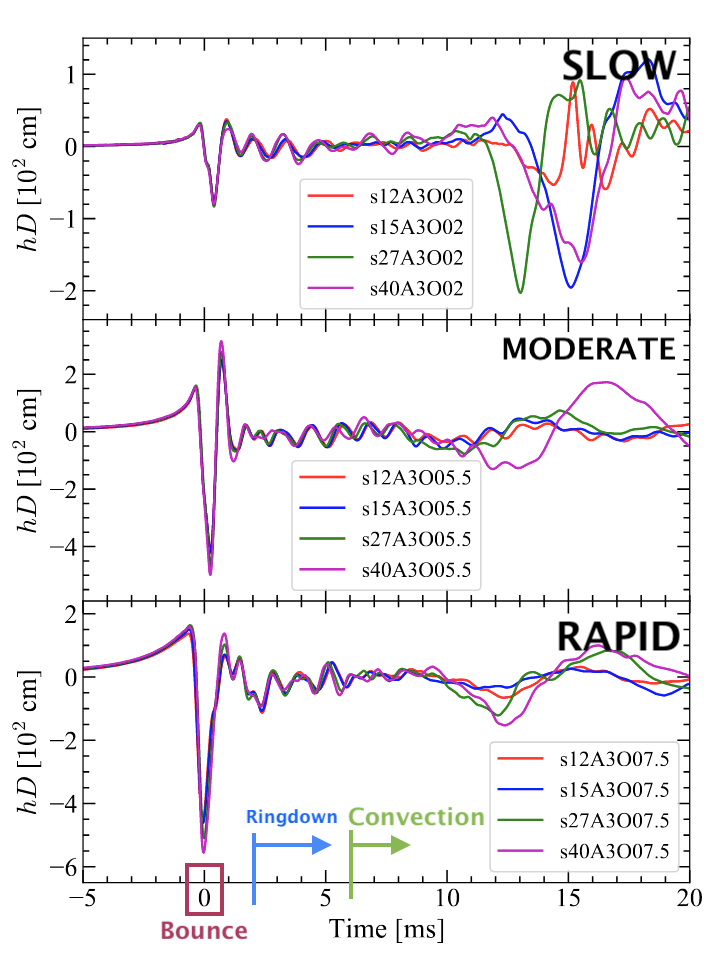
The authors find that there are very few physically discernible differences between the ZAMS masses when considering GW strains of this duration (Figure 3). This can possibly imply that the information supplied by the gravitational waves, such as the strength of the bounce, was not enough to represent the iron core at the time of the star’s death. (Iron core mass is a quantity related to the ZAMS mass, Figure 1.)
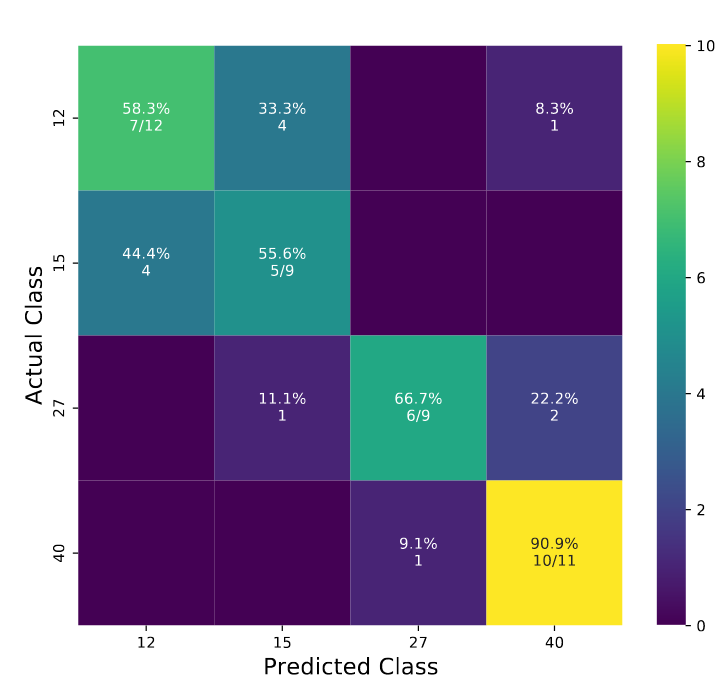
Additionally, they find the ML algorithm was best able to classify more accurately using the waveform information that spans -2 to 6 milliseconds (Figure 2). To convince yourself of this, revisit Figure 2 and ask yourself which areas were the most reproducible between SNe, and which portions of the wave are unique to an individual explosion. The latter proves difficult to anticipate for each new explosion that nature creates.
The most important difference among all the waveforms, in the eyes of the ML, takes place at around 2.5ms. Physically, this area of the waveform is called “ringdown” which is when the formed corpse is relaxing into its static rotation (Figure 2). The fact that this moment is important to the ML classifier means the difference in initial masses (one of the knobs the authors turned) influences the properties of the proto-neutron star, giving the algorithm some defining feature to tell the GW strains apart from one another and classify the progenitor.
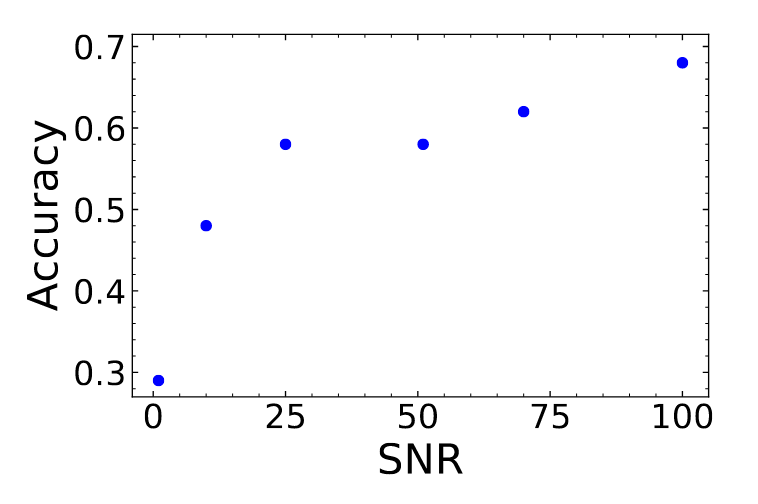
After training and testing their random forest classifier on over 400 waveforms of varying GW signal strength (or SNR), the authors conclude that there was still not enough information to say for certain what ZAMS mass each of the waveforms began with. Despite testing their algorithm on loud signals of SNR up to 100, they were unable to use this portion of the waveform to identify with over 70% accuracy (Figure 4). They conclude that this means the bounce and early ringdown alone are not enough information to determine the iron core mass of the star at the end of its life (related to the progenitor mass) and instead may require a multimessenger neutrino observation or more GW information like a longer signal.
Astrobite edited by Katya Gozman, Lili Alderson, and Mark Popinchalk
Featured image credit: Edited from NASA, ESA, J. Hester and A. Loll (Arizona State University) – HubbleSite: gallery, release.