
Dionysios Gakis is a junior at the University of Patras, Greece, studying Physics. This research was conducted as part of the activities of the Theoretical Astrophysics Group at his home institution, under the supervision of Professor Konstantinos N. Gourgouliatos, and was published in these papers: Celest. Mech. Dyn. Astron. 134 (2), 14 and A&A 670, A152
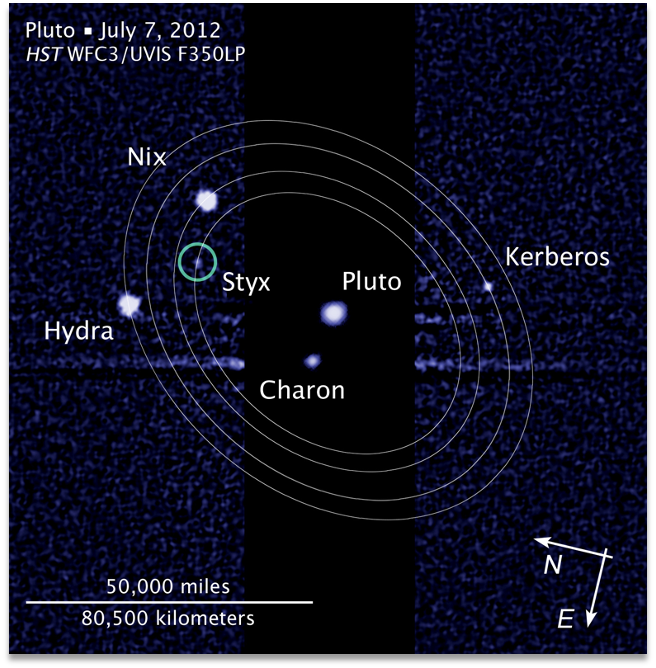
The dwarf planet Pluto and its largest moon Charon form a binary system, as their center of mass lies outside both objects. Around their barycenter, four recently discovered moons are orbiting: Styx, Nix, Kerberos and Hydra (Figure 1). However, modeling their orbits as typical Keplerian elliptic ones is not realistic because orbits around binary systems cannot be described the same way as orbits around a single body. Additionally, the moon orbits are strongly affected by the gravitational interactions between each other. For these reasons, we employ numerical simulations of the moon motions, using an n-body code, and compare our results against the semi-analytic model by Lee & Peale 2006, accounting for circumbinary orbits.
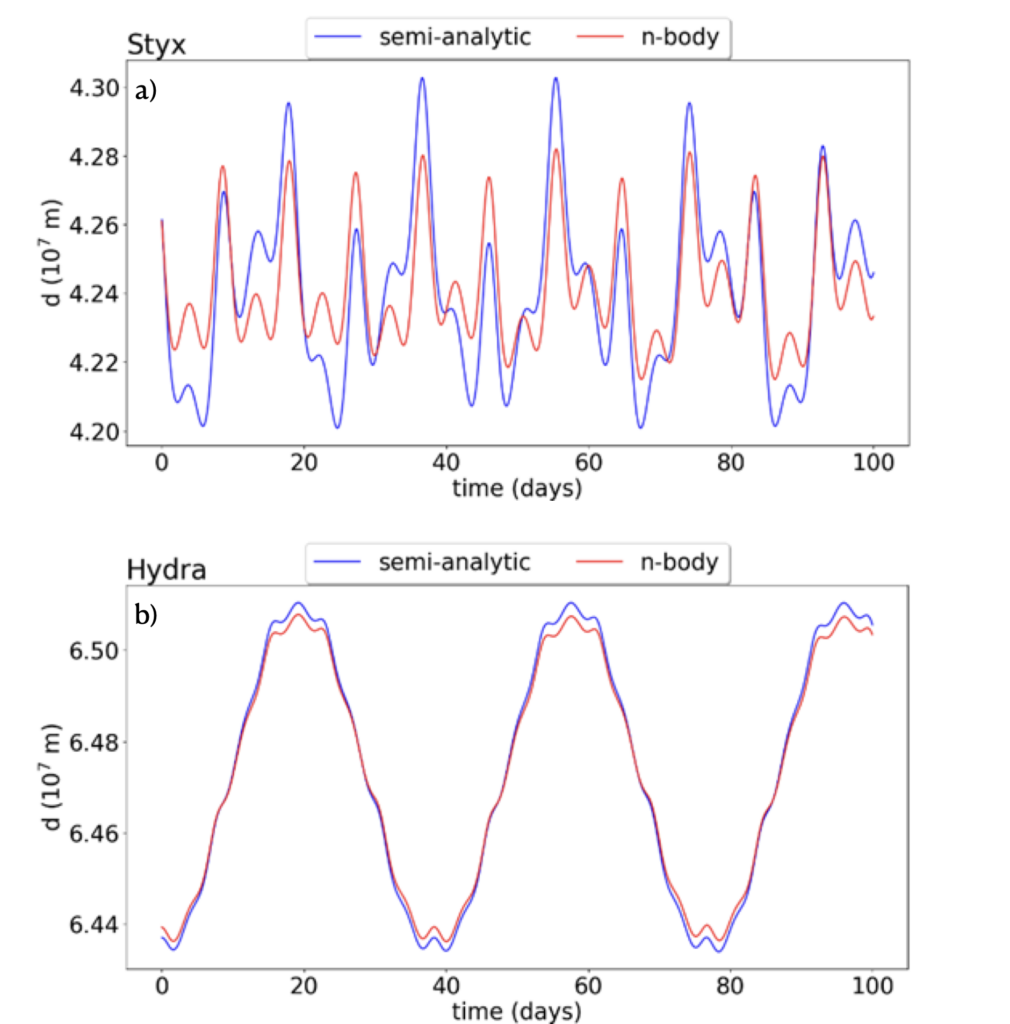
In Figures 2a and b, the variations of the orbital distance through time for Styx (the closest moon to the binary and the lightest one) and Hydra (the farthest and heaviest moon) are presented. Red lines correspond to the orbits obtained numerically, whereas the blue lines mark the outcomes of the semi-analytic model. At first, we notice that we cannot indeed use the typical Keplerian elements like the semi-major axis and eccentricity to describe the circumbinary orbits, as the central potential by the dwarf binary forces the small moons into several oscillations. Even when trying to enforce a zero-orbital eccentricity, distances appeared to have many inevitable fluctuations through time.
Moreover, the motions of the four small moons are a superposition of both forced oscillations by the binary system and mutual gravitational interactions. This is particularly visible for the less massive Styx, where the numerical and theoretical methods have major discrepancies, which is not the case for Hydra, which is almost unaffected by the reciprocal effects.
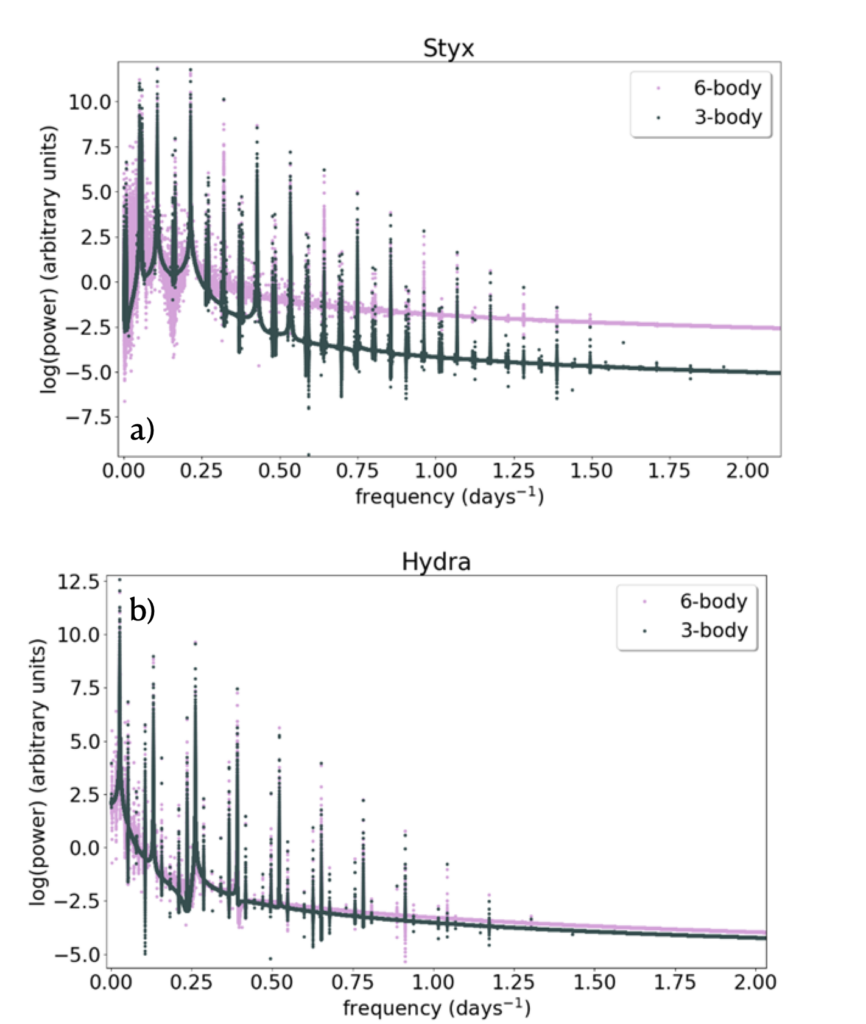
To separate the mutual gravitational effects from the central potential perturbations, we ran an extra set of 3-body simulations (i.e. containing the binary system and only one of the moons) in addition to the typical 6-body ones (containing the entire system). Next, we decomposed the resulting orbits into their frequencies using fast Fourier transforms (FFT). FFT is a powerful algorithm that enables us to separate the individual modes that come together to form a more complicated motion and assess their relative strengths. Results are shown in Figures 3a and b for Styx and Hydra, respectively (the purple plot arises from the 6-body situation and the black one from the 3-body one). Each of those formed peaks corresponds to a frequency. We conclude that the mutual effects induce many long period perturbations, especially for the lighter moons, whereas the binary effects mainly dominate in the high frequency region. These outcomes imply that in short timescales (i.e. a few orbital periods) the binary potential mainly controls the motions of the moons, but regarding their long-term evolution one needs to consider the gravity between each other moon too.
Edited by Jenny Calahan




This was a great summary! I’m always excited to see astrobites on the Kuiper Belt and orbits.
This summary also made me think of a writing style guide question and I’m wondering if anyone knows the standard/best practice.
For something like “moon orbits” where “moon” acts as the noun as adjective and “orbits” is the noun, is there a good adjective for moons in general like how “planetary” is the adjective for planets? Since “orbits” is also a verb, I think it’s useful to have an adjective like “planetary orbits” or “cometary orbits.”
Maybe this isn’t a real problem, but it’s something that I’ve been thinking about.
Again, great summary!