Shifting the Gravitational Wave Background

by | Nov 24, 2023 | Daily Paper Summaries | 0 comments

Title: Kinematic anisotropies and pulsar timing arrays

Authors: Gianmassimo Tasinato

Author Institution: Dipartimento di Fisica e Astronomia, Universita di Bologna and Physics Department, Swansea University

Status: Submitted to arXiv

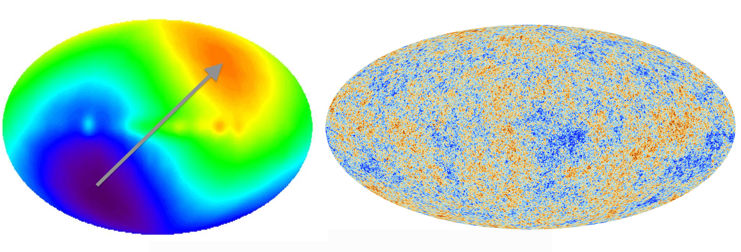
The solar system is not at rest within our galaxy. In fact, neither our galaxy nor our local group of galaxies are at rest in the universe. Our motion affects all of our astronomical observations. For example, our motion with respect to the rest frame of the cosmic microwave background (CMB) – the first light that traveled freely through the universe– produces a dipole in the temperatures of the photons we observe. This effect is illustrated in the full-sky map of the CMB shown in Figure 1. In the left image, the upper right appears hotter and the lower left appears cooler, due to the shortening (Doppler blue-shifting) and lengthening (Doppler red-shifting) of observed wavelengths as we move toward and away from the CMB radiation, respectively. This temperature difference is the CMB dipole, and its amplitude and direction together tell us our velocity with respect to the rest frame of the CMB photons. This dipole must be removed in order to study the fluctuations that are intrinsic to the CMB.

One would expect our velocity to affect observations of other types of radiation from the early universe as well. Of particular interest is a gravitational wave background (GWB) with a cosmological source, such as inflation or a cosmological phase transition, which may account for at least part of the signal recently detected by pulsar timing arrays. The author of today’s paper explores what information the effects of this motion might be able to tell us about the GWB.

Figure 1. Left: CMB dipole. The upper right appears hotter (more red) and lower left appears cooler (more blue) due to the Doppler effect, which alters the observed wavelength of the photons as we move toward (blue-shift) or away (red-shift) from them. The gray arrow illustrates the direction of our motion. Note that the temperature key (blue=cooler, red=hotter) is the opposite of the Doppler shift names, such that we move away (red-shift) from the blue region and towards (blue-shift) the red region. (Image Credit: DMR, COBE, NASA, Four-Year Sky Map, modified by author) Right: ‘intrinsic’ CMB temperature fluctuations, (blue = cooler, red=warmer) after the dipole and foreground are removed. (Credit: ESA and the Planck Collaboration) The temperature scale is about 10 times smaller in the map on the right.

PTA Response

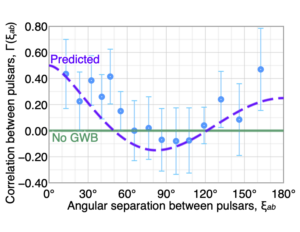
Figure 2: The correlation of GWB signals in pulsars as a function of the angle between pairs of pulsars. The purple dashed line shows the HD curve, the theoretical prediction for an isotropic and unpolarized GWB in general relativity. The NANOGrav 15-yr data (blue) strongly supports a HD curve. (Credit: Cmglee/Wikimedia)

A pulsar timing array (PTA) is a set of pulsars monitored by radio telescopes and analyzed to search for tiny shifts in the expected arrival times of their pulses, which can be the result of passing gravitational waves (GW). The response of a PTA to a GWB is commonly described by the Hellings and Downs (HD) curve, shown in Figure 2. The HD curve describes the response of pairs of pulsars to an isotropic (same in every direction) and unpolarized (no preferred GW polarization) background of gravitational waves in general relativity, as a function of the angular separation of the pulsars. Break any of these assumptions– isotropy, no net polarization, or general relativity– and the expected signature deviates from the HD curve. Even if these assumptions are true in the GWB source’s rest frame, if we are moving with respect to this frame, a directional dependence (aka anisotropy) will appear in our observations.

Today’s paper breaks down the response of an array of pulsars to properties of a GWB in three categories: intensity, circular polarization, and modified gravity, all in the case of the observer moving with respect to the GWB.

Intensity

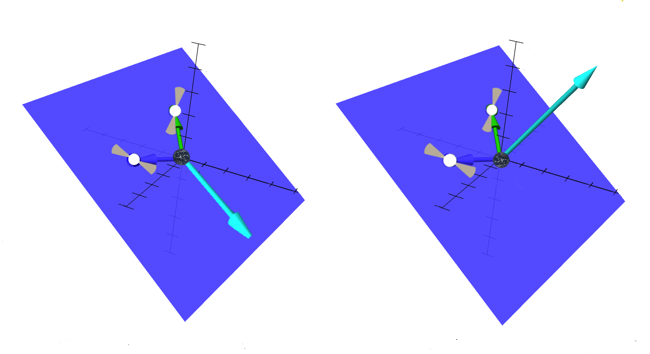
If the observer has a relative velocity with respect to the rest frame of the GWB’s source, the pulsar responses to the intensity of the GWB will still follow an HD curve to a first approximation. Deviations from the HD curve appear in higher order terms, which are weighted by factors of the relative velocity between the two frames. The first modification controls the dipole anisotropy from the Doppler motion. This term is proportional to the slope of the GWB’s intensity as a function of the wave frequencies. Measuring the dipole in the PTA signature would then allow us to extract more information about the GWB’s intensity profile, namely its slope. Furthermore, the dipole contribution depends on the angle between the pulsar pairs and the velocity between the frames, in addition to the angle between the pulsars as seen from Earth. Notably, the vectors describing the pulsar positions must have components in the same direction as the velocity between the frames in order to induce an anisotropy in the GW intensity. The effects of the motion are maximized for pulsar pairs lying in the same plane as the relative velocity, and vanish for pulsar pairs in a plane orthogonal to the relative velocity. See Figure 3.

Figure 3: Geometry. The plane of the pulsar pair (purple shaded) is formed by the vectors (blue and green arrows) between the Earth (placed at the origin) and two pulsars. Possible relative velocities between the observer (Earth-pulsar system) and GWB rest frame is given by the cyan arrow. The diagram on the left shows a velocity lying in the ‘pulsar’-plane, which maximizes the Doppler effect on intensity, and the right diagram shows a velocity orthogonal to the plane, maximizing the effect on circular polarization. (Photograph of Earth from NASA; figures not to scale)

Polarization

Polarization describes the orientation of the stretching and squeezing of space as a gravitational wave travels. Circular polarization of a cosmological GWB indicates parity-violating effects in the early universe. Parity violation is needed to explain why there is more matter than antimatter in the universe today, and appears in a variety of interactions in models beyond general relativity and the standard model of particle physics. This makes polarization an interesting and exciting property of the GWB to search for. Previous work has shown that circular polarization is very difficult or even impossible to detect with single interferometer experiments (like LIGO-VIRGO or LISA) when focusing only on the isotropic part of the background. Anisotropies improve the detection prospects, and in the case of PTAs, anisotropies are required to detect circular polarization of a GWB. Today’s paper shows that the Doppler-induced anisotropy may be able to probe circular polarization with PTAs.

Unlike the GWB’s intensity, its circular polarization has a vanishing contribution to the pulsar response function if the background is isotropic. Geometrically, the polarization signals cancel out over the full sky. We need an anisotropic signal to prevent this and measure the polarization. The dipole anisotropy from the relative motion between the Earth-pulsar system and the rest frame of the GWB allows this. Accounting for the Doppler motion, the PTA response function gains a term proportional to the slope of the GWB’s circular polarization frequency profile. Opposite to the pulsar response to intensity, a pulsar pair can only detect circular polarization if the relative velocity between frames has components orthogonal to the plane formed by the pulsar directions, such as in the example on the right side of Figure 3.

Figure 4: Figure 1 of the paper. Contributions to the PTA response functions to GWB intensity (dashed blue) and circular polarization (dot-dashed red) are compared to the HD curve (solid black). Note that compared to Figure 2 above, \(\Gamma\) is normalized differently and angle \(\xi\) is given in radians rather than degrees. This figure ignores the geometrical factors, which depend on the angles between the planes formed by the pulsar pairs and the relative velocity between the frames.

In addition to circular polarization, there are extra polarizations predicted by alternative theories of gravity. The author finds that the dipole anisotropy may be able to provide information about the existence of these. If the GWB profiles belonging to certain of these extra polarizations have steep slopes or other pronounced features, then their presence may be detectable in PTA data.

Outlook

We should expect a GWB of cosmological origin to have anisotropies due to our motion with respect to its source. These anisotropies will lead to a PTA response that deviates from the HD curve in a way that depends on the properties of the GWB, and measurements of these deviations can be calculated analytically in order to extract more information from the signal. The findings presented in this paper could be useful in planning future measurements or selecting existing data to use anisotropies to detect or set more stringent constraints on parity violation in gravitational interactions, the presence of extra polarizations, and the frequency profile of the GWB. TL;DR pulsars can be used to extract information about new and exotic physics from GWBs!

Astrobite edited by Evan Lewis

Featured image credit: Earth photograph from NASA, modified by author

Author

  • Emma Clarke

    I am a 4th year physics PhD student at Carnegie Mellon University. My research focuses on gravitational waves from the early universe, in particular signals from MHD turbulence at phase transitions. Outside of the office, I can be found figure skating, practicing Ashtanga, reading, writing fiction, and baking.

    View all posts

Submit a Comment

Your email address will not be published. Required fields are marked *