- Title: Upper Limits on the Isotropic Gravitational Radiation Background from Pulsar Timing Analysis
- Authors: R. W Hellings and G. S. Downs
- First Author’s Institution: Jet Propulsion Laboratory, California Institute of Technology
- Paper Status: Published in The Astrophysical Journal (1983)
The gravitational-wave Universe has at long last been unlocked: LIGO’s recent observations of gravitational radiation from binary black hole mergers have given astronomers a new means to observe the cosmos. With the influx of papers that pursued these detections over the past half year, it is easy to assume that gravitational-wave physics is a research topic exclusive to recent times. In reality, this research field has a rich history, and the methods used to detect gravitational waves were developed over many decades. For example, the idea of using interferometers like LIGO for gravitational-wave detection got its roots in the 1960s, and took nearly half a century to evolve from an idea to an observation. Today’s Astrobite will take us back to a classic astrophysical paper that delivered a crucial result for the future of gravitational-wave astronomy.
Ground-based interferometers are not the only way that scientists are working to detect the ripples of spacetime. Analogous to light, gravitational waves come in a range of frequencies, and require unique methods and technologies to unveil the diverse array of astrophysical sources. LIGO and other ground-based interferometers are sensitive to high-frequency gravitational waves (from about 10 Hz to 1000 Hz). Though improving instrumentation and adding more detectors to the network will increase the sensitivity of LIGO in this frequency range, ground-based interferometers will always be insensitive to gravitational waves below 10 Hz due to the rumbling and grumbling of the planet on which they sit.
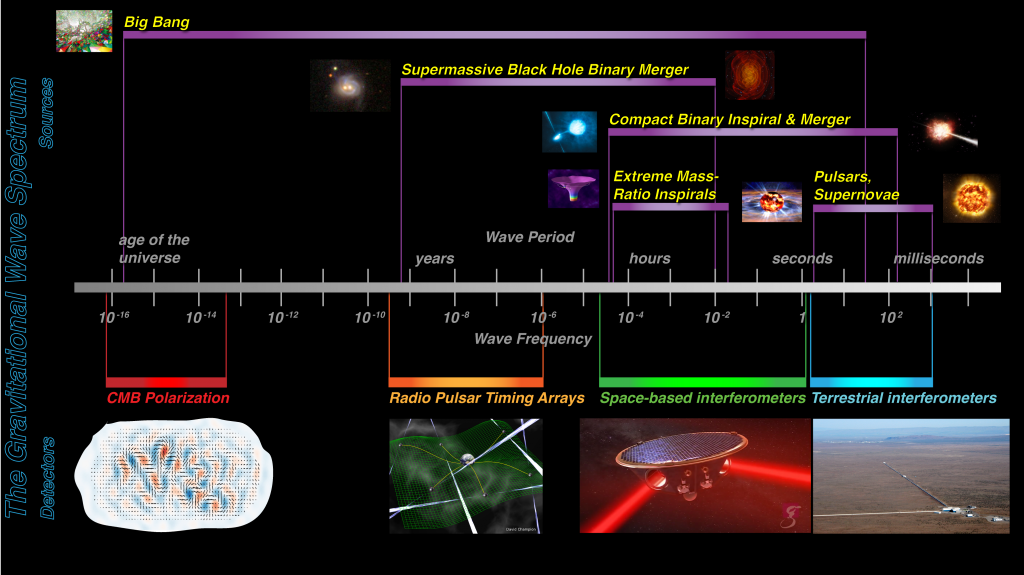
The full spectrum of gravitational-wave emission. The line in the middle of the image shows the periods of gravitational waves that are believed to be generated by associated objects and events at the top of the image, and the bottom of the image illustrates techniques used to detect gravitational waves at these different frequencies. Credit: NASA/J. I. Thorpe.
Pulsar Timing Arrays (PTAs) provide one method for detecting lower-frequency gravitational waves, from about Hz. Pulsars are rapidly-rotating neutron stars that act as lighthouses, beaming a pulse of radiation at Earth once per rotation. The rotations of many pulsars are incredibly stable, allowing the repeated pulses of radiation to be used as a precise astrophysical clock. PTAs utilize high precision measurements of pulsar pulse periods to detect gravitational waves. A pulsar and Earth can be thought of as two ends of a gravitational-wave antenna, where the relative motion of Earth and the pulsar (say, by the stretching and squeezing of space from a passing gravitational wave) is monitored by observing the Doppler shift of pulse arrival times. This Doppler shift therefore acts to alter the period of the pulses received at Earth. PTAs can be leveraged to detect a stochastic background of supermassive black hole mergers – the culmination of gravitational waves from many such events occurring in the distant universe.
By subtracting the observed pulse arrival times with the expected arrival times (known as timing residuals), pulsars can provide information about the stretching and squeezing of space caused by a gravitational wave (known as the strain) at Earth and at the pulsar. However, this is relatively useless on its own due to the inherent noise in each pulsar’s pulses. The real strength of PTAs comes from comparing the timing residuals of pulsars in different parts of the sky, since data from all the pulsars in the array will carry common information about the gravitational-wave strain at Earth. PTAs rely on cross-correlation of pulsar data, which essentially is the comparison of timing residuals from one pulsar with residuals of other pulsars in the array. By cross-correlating residuals of multiple pulsars at a given time, one can potentially detect a gravitational-wave signal by leveraging the common influence of background gravitational waves against unwanted, uncorrelated noise.
In the early 1980s, Hellings and Downs dug into the equations for correlating pulsar timing residuals. They found that, by assuming the stochastic gravitational waves come from all directions (i.e. isotropic) and the combination of background gravitational waves no longer carry any polarization information, the cross-correlation of timing residuals goes from being a very nasty integral to a mildly nasty integral. The solution gives the correlation in timing residuals, which is solely a function of pulsar angular separation:
where is the residual correlation of two pulsars (labelled i and j), and
is the angle between the two pulsars. Plotting this function over angular separation gives the famous Hellings and Downs curve.
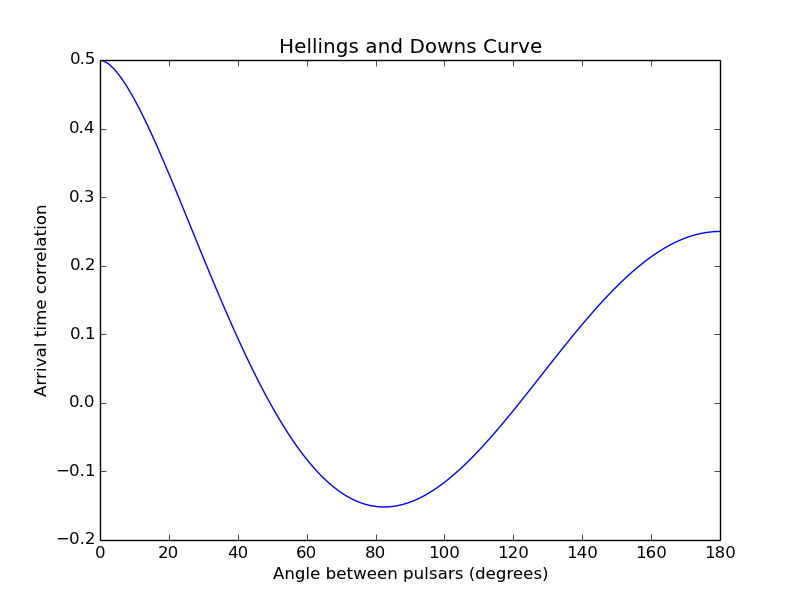
Hellings and Downs curve. This curve gives the pulse arrival time correlation as a function of angular separation in the sky. Credit: my mediocre plotting skills.
This curve gives the arrival time correlation of PTA pulsars – telling us exactly what we should see when we cross-correlate timing residuals of pulsars in the presence of a stochastic gravitational-wave background!
One thing I found particularly fascinating in this classic paper is that Hellings and Downs decreased the upper limit of gravitational wave energy density from a stochastic background by over 5 orders of magnitude, using their correlation analysis with just 4 pulsars! (For reference, the diameter of the Earth is about 5 orders of magnitude smaller than the distance between the Earth and the Sun). Though the Hellings and Downs curve has yet to be uncovered using PTAs, continued investigation keeps lowering the upper-limit on the energy density of the stochastic gravitational-wave background. This in turn reveals information about supermassive black holes in the universe and how often (if ever) they merge. Since the 1980s, this upper limit down has been brought down by another 4 orders of magnitude at the gravitational-wave frequencies which PTAs are sensitive, and many believe that the stochastic background should be detected by PTAs in the near future.
Cover image credit: David Champion

Trackbacks/Pingbacks