- Paper title: The Exoplanet Census: A General Method, Applied to Kepler
- Authors: Andrew N. Youdin
- First author’s affiliation:Harvard Smithsonian Center for Astrophysics, Cambridge, MA
Summary
In the paper, Youdin applies the statistical methods of Tabachnik & Tremaine (2002) to the Kepler dataset to compute the planetary distribution function, the distribution of exoplanets as a function of planet radius and orbital period. After performing a maximum likelihood analysis, Youdin determines powerlaw indices for the period and radius distributions of the Kepler sample. He finds a best fit radius powerlaw index of -1.73 +/- 0.07 (similar to the value of -1.92 +/- 0.11 derived by Howard et al. 2011) and a best fit period powerlaw index of 1.33 +/- 0.03. Intriguingly, Youdin reports a lack of medium-sized (~3 REarth) planets with orbital periods less than ~7 days and suggests that the lack of medium-sized planets might be due to evaporation of Neptune-sized that are unfortunate enough to migrate too close to their host star.
The Sample
Youdin restricts his analysis to the planets in the Kepler sample with orbital periods between 0.5 days and 50 days, radii between 0.5 REarth and 20REarth, and detection signal-to-noise ratios >10. He also requires that the host stars have temperatures between 4100 K and 5100 K, surface gravity log g between 4.0 cm/s2 and 4.9 cm/s2, and Kepler magnitudes equal to or brighter than 15. The stellar criteria are identical to the criteria used by Howard et al. (2011) to define the “Solar subset.” Since Youdin uses detection efficiencies (discussed below) from Howard et al. (2011), his restrictions on the candidate planets and host stars are set by the cuts used in Howard et al. (2011). If you haven’t yet had a chance to read Howard et al. (2011), check out this astrobite for a great summary.
Selection Effects
As mentioned in the Summary, Youdin follows the maximum likelihood method of Tabachnik & Tremaine (2002) to determine the planetary distribution function. In order to conduct his analysis, he first parameterizes the selection effects in the Kepler survey using the following three parameters:
- The probability that the planet will transit as seen by Kepler.
- The probability that Kepler will be able to detect the transit.
- The probability that a reported transiting planet is a false positive.
Given the low false positive rate of Kepler (Morton & Johnson 2011), Youdin opts to neglect the third parameter. He determines the first parameter from the ratio of the host star radius to the planet’s semimajor axis and then fits a broken powerlaw to the detection efficiencies reported by Howard et al. 2011 for 1-16 REarth planets with periods between 0.68 days and 50 days in order to determine a functional dependence for the detection efficiency for all planet radii between 0.5 REarth and 20 REarth and for all orbital periods between 0.5 days and 50 days. The detection efficiencies from Howard et al. 2011 and Youdin’s powerlaw fit are plotted in the figure below in terms of the ratio for discoverable planets to non-discoverable planets.
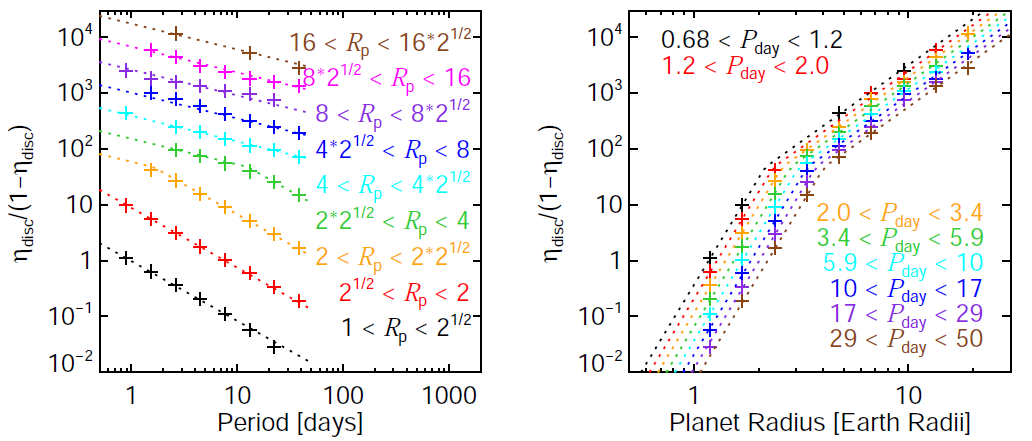
Broken powerlaw fits to the ratio of discoverable planets to non-discoverable planets. The crosses mark the values reported by Howard et al. 2011 and the dashed lines indicate fits for each radius or period range. Left: Discovery efficiency as a function of orbital period. Right: Discovery efficiency as a function of planet radius. Figure 2 from Youdin 2011.
Results
In addition to investigating the full sample, Youdin also divides the sample into small planets (R < 3REarth), big planets (R > 3REarth), fast planets (period 7 days). He repeats the maximum likelihood analysis for each subsample and then determines the best-fit powerlaw indices. As shown in the left panel of the figure below, Youdin finds that the radius powerlaw for small planets in short-period orbits is only slightly steeper than the radius powerlaw for small planets in long-period orbits, but that the radius powerlaw for big planets in short-period orbits is significantly flatter than the radius powerlaw for big planets in long-period orbits. In the right panel of the figure, Youdin displays the number of planets per star per logarithmic interval in orbital period. He finds no significant difference between the powerlaw indices for small planets and big planets in a given period range. For both size ranges, the period powerlaw flattens at longer orbital periods.
These results imply that the number of small planets for every big planet increases with increasing orbital period. As shown in the green histograms (big, fast) in the figure, there is a noticeable decrease in the number of medium-sized (~3 REarth) planets at short period orbits (<7 days). The low abundance of ~3 REarth planets in short period orbits indicates that those planets either do not form or migrate in such short period orbits or that they are quickly destroyed after formation or migration. Youdin proposes that one explanation might be that “lesser” giant planets, unlike hot Jupiters, are not massive enough to retain their atmospheres at such close separations and therefore evaporate away leaving only rocky cores.
Conclusions
After fitting powerlaws to the Kepler data, Youdin finds that the planets with radii between 0.5 REarth and 20Earth and orbital periods less than 50 days are so common that the average number per star is 0.7-1.4! Youdin’s result is consistent with the lack of short period planets in the solar system because, as Youdin points out, many of those planets might orbit the same star as part of a multiple planet system (Lissauer et al. 2011). Extrapolating the occurrence rate of small planets out to one year orbital periods, Youdin finds that the average solar-like star hosts ~3 Earth-like planets with orbital periods less than one year. That’s fantastic news for astrobiology, but it remains to be seen whether the occurrence rate of Earth-like planets in long period orbits can be described by the same power law as the occurrence rate of Earth-like planets with shorter orbital periods.

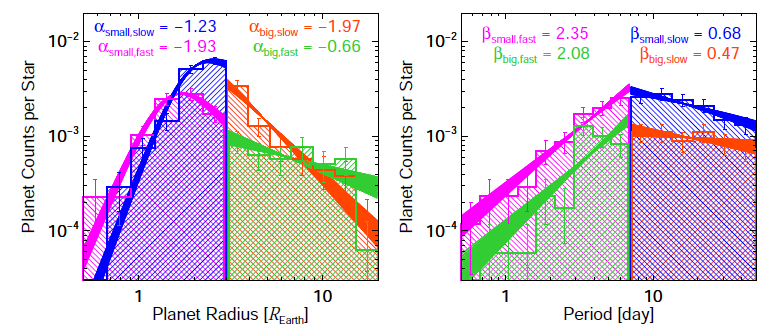
Thanks for your excellent summary of my paper. I don’t have much to add other than to point the interested reader to the resulting size distributions in Fig. 7 of the paper. These show a remarkable deficit of ~3 R_Earth planets at the shortest periods. This could be a signature of atmospheric evaporation, or a completely new theory may be needed!
Thanks, Andrew. The lack of intermediate size planets is intriguing and I’m curious to see what new theories will be proposed to explain their absence.