Title: LARES Successfully Launched in Orbit: Satellite and Mission Description
Authors: Antonio Paolozzi and Ignazio Ciufolini
First Author’s Institution: Scuola di Ingegneria Aerospaziale, and DIAEE, Sapienza Università di Roma
Einstein’s General Relativity is one of the most widely-tested theories in all of physics. Einstein himself proposed the three classical tests of the theory: The precession of Mercury’s orbit, the deflection of light by the sun, and the gravitational redshift of light, all of which are observed to match the predictions of General Relativity to remarkable precision. To this day we continue to look for possible cracks or missing pieces in the Theory through more modern tests.
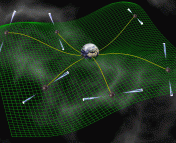
Geometrical depiction of Frame Dragging. Source.
One of the predictions of the General Theory of Relativity is an effect called Frame-Dragging. It is also known as Lense-Thirring precession, after the folks who formulated it in 1918. When a massive object–like a star or a planet, or even a black hole–rotates, it literally drags space-time around it. Think of a spinning bowling ball suspended in molasses. If you put some sort of test particle near the bowling ball, the molasses which is being dragged with the bowling ball will also drag the test particle. This effect becomes less prominent with distance; the farther away from the bowling ball the test particle is, the less noticeable the effect. In the real world, the bowling ball is, say, the Earth, the test particle is an orbiting satellite, and the molasses is space-time. If you calculated the orbit of the satellite based on Newton’s Laws, you would find that after some time your predictions were wrong, because the satellite is getting that extra push from the dragging of space-time around it.
Generally, the frame-dragging effect is quite subtle—at least compared to other effects like atmospheric drag or gravitational field inhomogeneities (due to the Earth not being a perfect sphere and of uniform density). It is for that reason that measuring the effects of frame-dragging has proven to be quite difficult. The Gravity Probe B (GP-B) spacecraft is perhaps the most well-known attempt at measuring the effect near Earth (although there have been a few others). GP-B was launched in 2004 and consisted of four delicate gyroscopes and a reference telescope. The telescope was pointed towards the star IM Pegasi as a reference point. Over time, the satellite would slowly change orientation, partly due to frame-dragging. The gyroscopes helped measure this minuscule change in orientation. Unfortunately, there were some unexpected sources of noise in the data and scientists have been working to model them and subtract them out before they can make the measurements they want. At present, their results agree with General Relativity, but their margin of error is roughly 19%.

A cartoon of the LARES satellite. The indentations represent the mirrors. Source.
The authors of today’s paper aim to measure frame-dragging to much greater precision and in a very cost-effective way. The satellite is called the LAser RElativity Satellite (LARES). Launched in February of 2012, its elegance lies in its simplicity. The satellite is passive—that is, it has no internal instruments that record and transmit data about its orbit. Instead, scientists are tracking it from Earth, by shining lasers on its mirror-covered surface. Basically, it’s a disco ball in the sky. This tracking processes is known as laser ranging, and we’ve been using it for a long time for a lot of things, like tracking the orbit of the moon, for example. That’s the easy part. The hard part is minimizing the other effects on the spacecraft that might interfere with measurements.
To minimize atmospheric drag and reduce the effects of other perturbations, the satellite boasts the smallest surface-to-mass ratio ever achieved. If that weren’t enough, its tungsten-alloy body gives it a mean density of 15,300 kg/m^3, making it the most dense object orbiting anything anywhere in the solar system. This small surface-to-mass ratio makes it the perfect test particle for this type of experiment, and the experimenters in charge are expecting to make measurements of frame dragging with an error of only 1%. Whether that level of accuracy will be achieved is not yet known. As the folks working on Gravity Probe B can attest, making these kinds of measurements is no walk in the park and unexpected errors have a way of springing up where they’re least expected.


The – preliminary but pretty clear nonetheless – outcome of this experiment was already reported at a conference in Germany last year: http://skyweek.wordpress.com/2012/10/11/eine-wolfram-kugel-im-orbit-bestatigt-frame-dragging-schon-auf-1-5-prozent-genau …
I believe there is no frame-dragging effect of gravity on mass, only on electromagnetic energy!
Curiously, the Lense-Thirring effect in Gravity Probe B has the same value than the geodetic effect of the Earth around the Sun.
NASA error?
An interesting experiment!
Understanding Gravity Probe-B experiment without math
http://www.molwick.com/en/gravitation/082-gravity-probe-b.html
http://www.molwick.com/en/gravitation/r-lense-thirring-frame-dragging.jpg