Title: A multiple-impact origin for the Moon (pdf)
Authors: Raluca Rufu, Oded Aharonson, Hagai Perets
First Author’s Institution: Weizmann Institute of Science
Status: Published in Nature Geoscience [closed access]
“What is it you want, Earth? What do you want? You want the Moon? Hey, that’s a pretty good idea! I’ll give you the Moon!” the solar system once said to the Earth not too long after our planet formed.
The Giant Impact Hypothesis postulates that our Moon arose from a catastrophic collision between the primordial Earth and a Mars-sized planet known as Theia with about a tenth of our planet’s mass. This idea was first proposed in 1946 and has gained significant traction due to the similarity of the Moon’s composition with that of the Earth, among other reasons. Specifically, several isotope ratios on the Moon — including oxygen — are identical to those on the Earth to within 0.01%. Unfortunately, recent simulations have shown that giant impacts rarely produce two objects that are so identical because the Moon often forms mostly out of material from the impactor, not the Earth. The similarity between the Earth and the Moon that helped inspire the Giant Impact Hypothesis has now become one of the most enigmatic mysteries to unravel.
Raluca Rufu, Oded Aharonson, and Hagai Perets — the authors of today’s paper — attempt to solve this problem by tweaking the original Giant Impact Hypothesis. Instead of forming the Moon from one giant impact, they suggest it formed from a series of medium-sized impacts spread out over millions of years.
The Moonlet Cascade
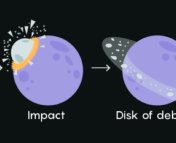
As Figure 1 shows, this new scenario begins the same way as the Giant Impact Hypothesis. First, a planetary embryo between the size of the Moon and the size of Mars hits the Earth, spewing an immense cloud of debris into orbit around our planet over a matter of days. The debris forms a disk that eventually coalesces into a tiny proto-Moon (which the authors call a moonlet) over the course of several centuries. During this time, the moonlet will also migrate away from the Earth as tidal dissipation slows down its rotation rate.
After a few million years pass, another embryo collides with the Earth, creating a new debris disk around the planet inside the orbit of the first moonlet. Once again, the disk will form another moonlet, which then migrates outwards and eventually merges with the first moonlet. The process repeats and after a few tens of impacts, the original moonlet will grow into an object the size of the Moon today!

Figure 1. Schematic for forming the Moon with multiple impacts. See description above.
Rufu et al. use smoothed particle hydrodynamics (SPH) to simulate the impacts themselves (see video below). Each impact takes just 24 hours of simulation time to figure out what fraction of the material ends up in the debris disk. The authors then determine each moonlet’s final mass by assuming that all of the material in the disk beyond the Roche limit will end up in the moonlet, while the rest of the disk that is too close to the Earth will rain back down onto our planet. They then use Monte Carlo simulations to create a random chain of 10, 20, or 30 small impactors that ultimately lead to a single moon.
Video. Sample SPH simulation of a single impact. The dashed line is the Roche limit.
Impact Outcomes
The authors simulate 864 different impact scenarios in which they vary four key parameters: (1) the impactor mass — from 1 to 9 Moon masses, (2) the impactor velocity — from 1 to 4 times the lowest possible impact velocity, (3) the impact angle — from -60 to 60 degrees, and (4) the Earth’s rotation rate.
In the Giant Impact Hypothesis, an impactor must hit the Earth head-on (close to zero degrees) at very high speeds (4 times the escape velocity) to spawn a moon that forms primarily out of the Earth instead of the impactor (and thus, with the same isotope ratios as the Earth). However, as Figure 2 shows, the multi-impact model allows the smaller impactors to collide at much lower speeds (2 times the escape velocity) over a much wider range of angles (between -30 to 30 degrees) and still end up with similar isotope ratios to the Earth.
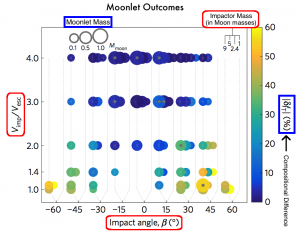
Figure 2. Moonlet properties (mass and compositional difference; circled with blue rectangles) for different parameters (impactor velocity, angle, and mass; circled in red). Outcomes for the four different impactor masses are spaced left to right at each impact angle (see top right). Marker size scales with moonlet mass (see top left). If the circle is missing, no debris disk formed. Circles that are bluer (<10%) are more likely to lead to the Earth and the Moon’s nearly identical isotope ratios. Adapted from Fig. 3b.
Overall, Rufu et al. find that at least 20 impactors are needed to create a Moon-mass object in 40% of these sequences. Moreover, 17% of these impact chains lead to a moon that is as compositionally identical to the Earth in terms of isotopes as the real Moon.
This model is better at matching the isotope ratios for two reasons. First, it is much more common for individual smaller moonlets to form mostly from Earth material than it would be for a Moon that forms from a larger giant impact. Second, the inherent reason why a chain helps is that each individual moonlet may have a higher or lower isotope ratio than the Earth, which helps the ratio average out towards the Earth’s value in the end.
Room for Improvement
The authors find it is more difficult to reproduce the present-day value of the total angular momentum in the Earth-Moon system. Only 10% of impactor sequences end with the system having as much angular momentum as we observe today. However, there is promise in the fact that 50% of the systems reach the present amount of angular momentum at some point during the sequence, just not at the end. This timing issue may be reconcilable since the angular momentum can increase or decrease drastically with each impact, and is set randomly by the properties of the last few impactors.
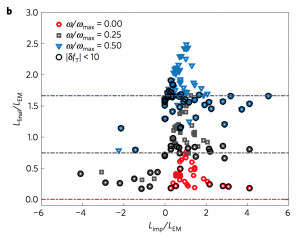
Figure 3. Final angular momentum outcomes of each individual impact relative to the Earth-Moon system’s total angular momentum (L_EM). Ideally, the impact should create a system with at least as much angular momentum (> 1.0 L_EM) as the Earth-Moon system currently has. Impacts that also have a small enough compositional difference <10% (see Figure 2) to account for the identical isotope ratios are circled. Adapted from Fig. 4b.
Furthermore, Rufu et al. caution that they do not simulate the formation of a moonlet from the debris disk or the mergers of the many moonlets. Instead, they assume that all of the material ends up in the moonlet and that the moonlets merge without losing material. They plan to address both issues in follow-up studies.
For now, the authors have shown that the Moon’s origin may be more complex than we thought. It may be awhile before we fully understand how the solar system gave us the Moon.
Featured Image Credit: Lunar and Planetary Institute



Why not Venus too? If ~20 impactors created mini moons around the Earth, isn’t it fair to assume that a few impactors should have made moons for Venus too? Obviously that didn’t happen.
If Venus had moons they are now lost because the (almost) tidal lock of Venus rotation.