Title: Tilted circumbinary planetary systems as efficient progenitors of free-floating planets
Authors: Cheng Chen, Rebecca G. Martin, Stephen H. Lubow, and C.J. Nixon
Institutions: School of Physics and Astronomy, University of Leeds
Access: eprint on arXiv
All planets orbit around stars.
Okay, that was a lie. But a hundred years ago, it seemed super true — we only knew of the 8 planets around our own Sun.
Then, later, it still seemed decently true. Astronomers started finding planets around other stars in the 1990s (which the opening statement supported!). At this point, though, the field had at least begun to consider that there could be a population of “free-floating planets” — planet-sized bodies wandering through space, unaffiliated with any particular star.
Because our methods of finding planets, at that point, relied on the dimming or shifting of a host stars’ light, these rogues seemed unknowable (if they existed at all). So perhaps the statement could be modified to read “all planets that we can detect orbit around stars,” which would still maybe hold a little truth.
As our telescopes (and our techniques) have improved, though, it has become very clear that the statement is… irredeemably untrue. Since the turn of the century, largely through a more direct observational technique called microlensing, we’ve gradually uncovered a rich population of free-floating planets dancing in the vast cosmic dark. (Just last month, JWST revolutionized yet another sub-field with its discovery of free-floating pairs of planets, but that’s a topic for another ’bite.)
Young, wild, and free: the instability of newborn planetary systems
But where do these unbound beauts come from? There are a few proposed mechanisms, but one of the most-likely methods involves planets forming around stars (like normal!) but subsequently being violently ejected from their bound orbits.
The period immediately following the formation of the planets is often suspected to be pretty messy. In the solar system, we think there was a major instability right after planets formed, in which our eight major planets interacted strongly with each other before settling into (roughly) the orbits they have today.
In fact, simulations of such an instability suggest that there could have originally been a fifth giant planet in the outer solar system, formed alongside Jupiter, Saturn, Uranus, and Neptune. During the period of unrest (often called a “late instability” due to its occurrence after planet formation was complete), this planet would have been “kicked” off of its original orbit — and ejected from the solar system altogether — through interactions with the other giants. Any such planet would, at this point, be a free-floater.
Today’s paper talks about these sorts of “planet-planet scattering” ejections, but it doesn’t talk about the solar system (nor any particular observed planetary system). Instead, in a common theorist tactic, the authors consider a whole class of planetary systems: those existing around two stars rather than one.
Two stars are better than one [for planetary ejections]
Just as planets can orbit stars, stars can orbit each other. And if their orbit is small enough, protoplanetary disks — and, thereafter, planets — can form around the pair of them. One of the most famous (fictional) examples of such a system is Star Wars’ Tatooine, which enjoys an iconic double sunset courtesy of the binary stars around which it orbits.
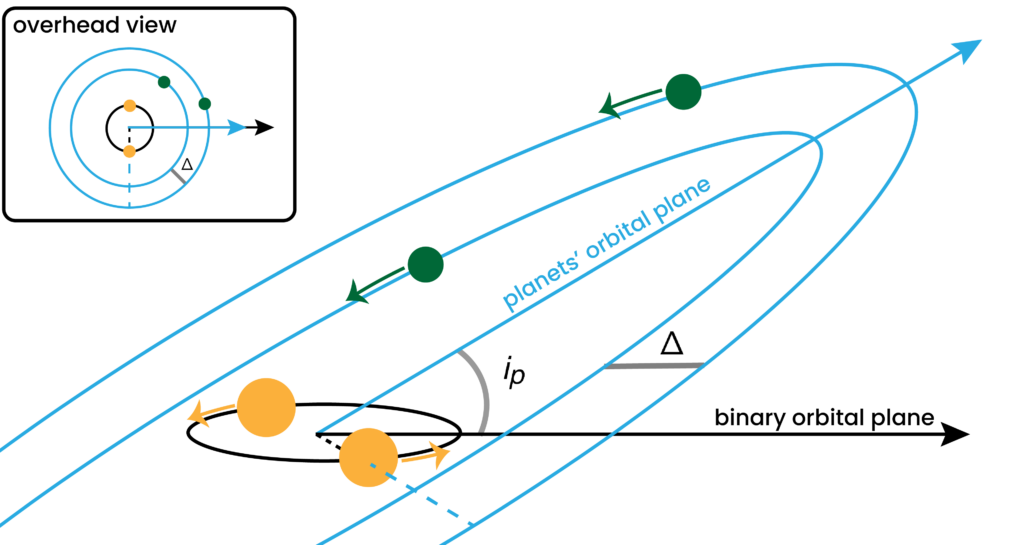
Ejections in planetary systems around single stars, though possible, probably don’t happen often enough to explain how common free-floating planets are. In dynamics, things can get a lot more complicated when you add just one extra body (see, e.g., the n-body problem!), so the authors of today’s paper wonder if adding another star will provide enough complication to eject more planets.
(This isn’t an unreasonable addition; binary pairs — and even binaries close enough to allow for planet formation — make up a significant fraction of all stars, so they’re definitely worth modeling.)
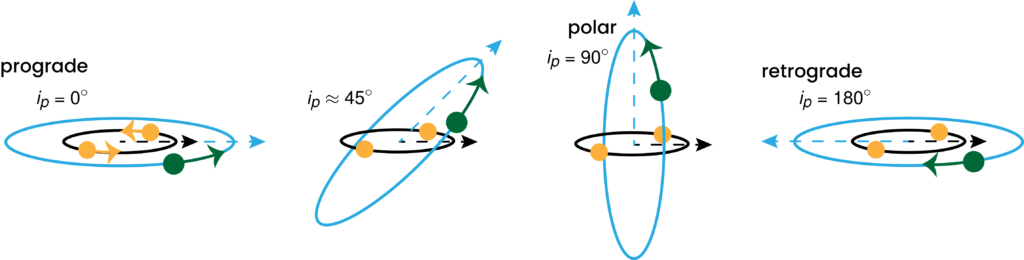
Specifically, the authors simulate planetary systems where two planets, separated by some distance, trace out orbits that are inclined relative to the orbit of the central binary stars (see Figures 1 and 2). They test systems with a range of initial inclinations, for a range of planet separations, for a select few choices of unequal planet masses. Through these simulations, they cover a broader range of “parameter space” (i.e., the ranges of values that a real-life system could have for its properties) than previous work.
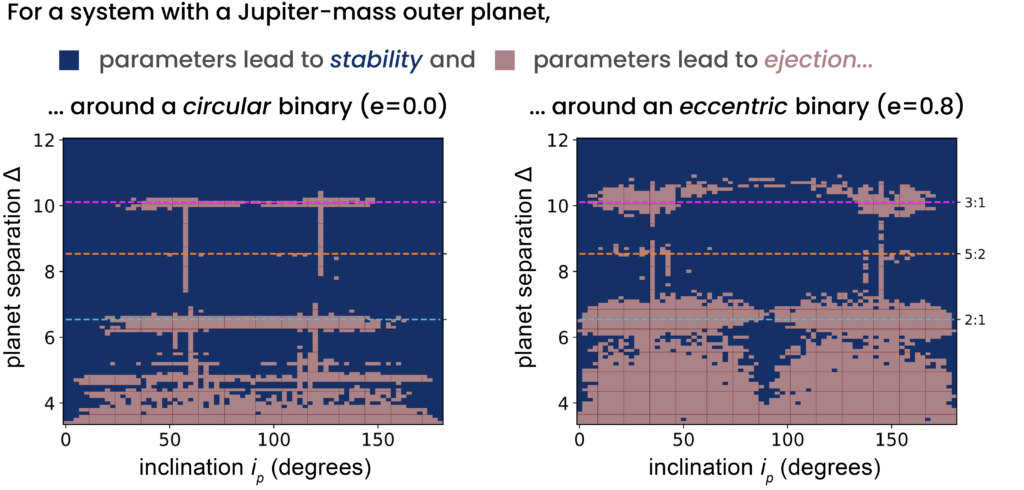
For all planet masses, the systems most likely to yield ejections involve close-together planets with orbits that are neither well-aligned (“prograde” or “retrograde”) nor perpendicular to the binary (“polar” — see Figure 2). Systems are much more likely to yield ejections when they have at least one planet more massive than Neptune, though the less-massive planet (if there is one) is always the one ejected. Eccentric binary stars — those orbiting each other on oblong, elliptical paths rather than perfect circles — also boost the ejection rate of the planets around them.
There are some fun planetary dynamics underlying these results! From the basic law of gravity, we know that more-massive, closer planets have more of an impact on others in their own system; it makes sense, then, that more-massive, closer planets cause more ejections. Oddly-inclined orbits (i.e., not prograde, polar, or retrograde) often lead to long-term oscillations in inclination; if the two planets take on different inclinations over the course of their lifetime, von Zeipel-Kozai-Lidov cycles can sometimes increase their eccentricity until one of them becomes unbound. And although ejections were most common among close-together planet pairs, they aren’t impossible with a bigger gap; instability can occur near mean motion resonances, where the periods of the two planets are integer multiples of each other (e.g., at the 2:1 resonance, the inner planet orbits twice as quickly as the outer).
A few more free-floaters
That all said, this isn’t an article about planetary dynamics — it’s about free-floating planets. These results show that a decent variety of planets can be ejected from planetary systems around binary stars, yielding a decent total occurrence rate for free-floaters from this mechanism. This is a decent win for planet-planet scattering as a potential source of unbound planets!
As in any theory paper, there’s work to be done to constrain exactly how often we expect these Tatooine-like systems to eject planets, as well as the range of masses we would expect these ejected planets to have. And in reality, the total population of free-floating planets almost certainly comes from some combination of several effects, each contributing their own subpopulations. But with recent and upcoming observations from Subaru Hyper Suprime-Cam, TESS, Roman, and JWST, there will certainly be no lack of data to which models like these can be compared.
Astrobite edited by Sahil Hedge.
Featured image courtesy of NASA/JPL.



Even with a low rate of planetary ejection from forming planetary systems, this is a process that has been going on for most of the Universe’s existence, and consequently, one would expect that the population of free-floating planets must be quite large.