Title: Research on establishing a joint time-scale of pulsar time and atomic time based
Authors: Xingzhi Zhu, Zhehao Zhang, Chengshi Zhao, et al.
First Author’s Institution: National Time Service Center, Chinese Academy of Sciences, Timekeeping Theory and Methods Laboratory; Key Laboratory of Time Reference and Applications, Chinese Academy of Sciences
Status: Published in MNRAS [open access]

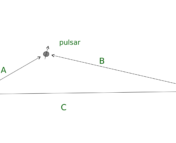
What time is it? For many applications, ranging from GPS navigation to interferometry-based astronomy, answering this question with extreme precision is crucial. To do so, one needs a highly stable clock. Currently, the most stable clocks are atomic clocks, which track time based on the resonance frequency of atoms, but they are not perfect. While they are very stable over short periods of time (months), their stability degrades over longer periods of time. To correct for this long-term instability, researchers have suggested using observations of millisecond pulsars (MSPs) as a supplementary clock. As MSPs rotate, electromagnetic radiation emitted from their magnetic poles sweep over the Earth like a lighthouse (illustrated in Figure 1). This radiation is observed as a regularly pulsed signal and exhibits remarkable long-term stability, which would serve as a fitting complement to the short-term stability of atomic clocks. Researchers have not yet found how to combine these two types of clocks in a way that outperforms atomic clocks alone, but in today’s paper, the authors introduce a promising new method to construct a joint timescale that combines the individual timescales produced by atomic clocks and MSPs.
It All Adds Up
The key tool the authors use in their work is a mathematical method known as wavelet analysis. Using this method, a signal can be decomposed into a sum of wave-like oscillations, or wavelets, each characterized by their position in time and their scale (i.e., how “stretched” or “squished” they are). For each wavelet, a coefficient representing “how much” of it is in the signal can be calculated by convolving the wavelet with the original signal. Not only can wavelet analysis be used to deconstruct a signal, but it can also be applied in the reverse direction to construct a signal from a set of wavelets and their coefficients
Making Good Time
In this paper, the authors use wavelet analysis to construct a joint timescale from an Ensemble Pulsar Time (EPT) based on 16 MSPs observed by the International Pulsar Timing Array (IPTA) (EPT) and the Atomic Time generated at the National Time Service Center, Chinese Academy of Sciences (TA(NTSC)). First, they decompose each time signal into wavelets at three different scales and calculate the coefficients associated with each wavelet. At every scale, they use the wavelet variance to characterize the stability of each time signal, then use these stabilities to compute a stability-weighted average time signal. They synthesize new wavelet coefficients from the stability-weighted average time signals at each scale, and finally use these new wavelet coefficients to construct a joint timescale the authors call Atomic Pulsar Time (APT).
Better Together
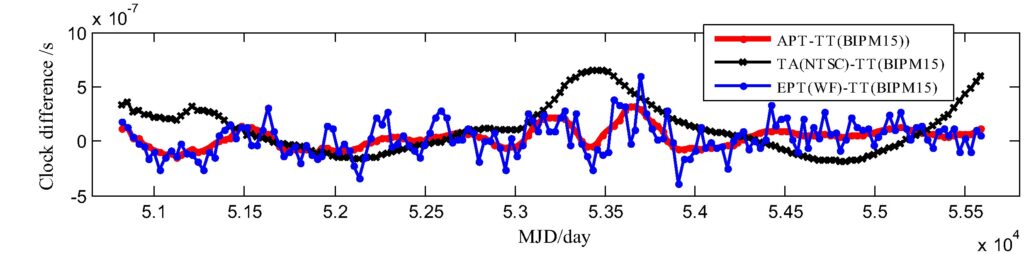
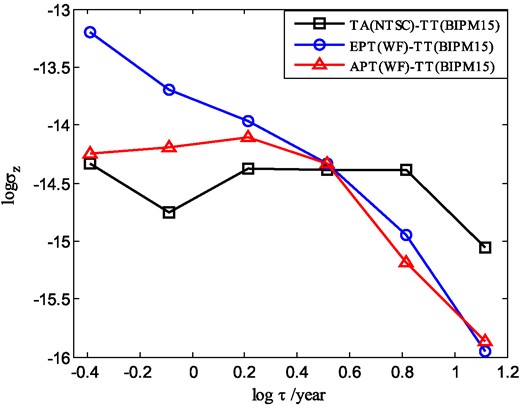
To assess the stability of APT compared to ETP and TA(NTSC), the authors examine the statistical deviation of the difference of each timescale and the Terrestrial Time calculated by the International Bureau of Weights and Measures published in 2015 (TT(BIPM2015)). Figure 2 shows the difference of APT, TA, and EPT with TT(BIPM15) over time. The difference between APT and TT(BIPM15) is minimal and much smaller than that of TA and TT(BIPM15), indicating that APT is smoother and more stable than TA. Figure 3 shows the stabilities of each timescale over time derived from the statistical deviation of the differences between the timescales and TT(BIPM15). The short-term stability of APT at 0.4 years is consistent with that of TA, and the long-term stability of APT closely resembles that of EPT while exceeding that of TA(NTSC), indicating that the unique stability advantages of both EPT and TA(NTSC) are preserved in APT. The authors further test this result further by experimenting with different methods for establishing EPT and find that the stability of APT could be improved by using more pulsars with smaller timing residuals and decreased low-frequency noise.
Overall, the authors have demonstrated the feasibility of using wavelet analysis to produce a joint timescale from atomic time and MSPs that retains the unique stability advantages of both atomic time and MSPs, and therefore outperforms them.
Astrobite edited by Caroline von Raesfeld
Featured image credit: Tonia Klein / NANOGrav