- Title: Scattering outcomes of close-in planets: constraints on planet migration
- Authors: Cristobal Petrovich, Scott Tremaine, and Roman Rafikov
- First Author’s Institution: Department of Astrophysical Sciences, Princeton University
As astronomers have found more and more exoplanets over the years, one thing has become clear: many planetary systems are quite different from our own. Super-Earths, Hot Jupiters, and giant planets on extremely large orbits were all surprising discoveries because no analogs to these exist in the Solar System.
Also surprising is the large fraction of exoplanets that travel on eccentric orbits; after all, the Solar System planets have fairly circular orbits (Mercury has the least-circular orbit with an eccentricity of 0.2, while the Earth has an eccentricity of only 0.02). This raises the question: how did so many exoplanets end up with eccentric orbits? One theory is that if planets get close to each other, they can interact gravitationally and “scatter” each other into eccentric orbits. But how likely is this to occur? Can it explain the number of eccentric planets we see?
The authors of this paper addressed the feasibility of this mechanism by running a large number of computer simulations. They began by assuming there were two “Hot-Jupiter” planets in the system, with initial semi-major axes between 0.05 and 0.15 AU. The authors ran the simulation 1,000 times, varying slightly the initial locations, eccentricities, and inclinations of the two planets, but always assuming the planets started in nearly circular orbits. The results are shown in the left panels of Figure 1.
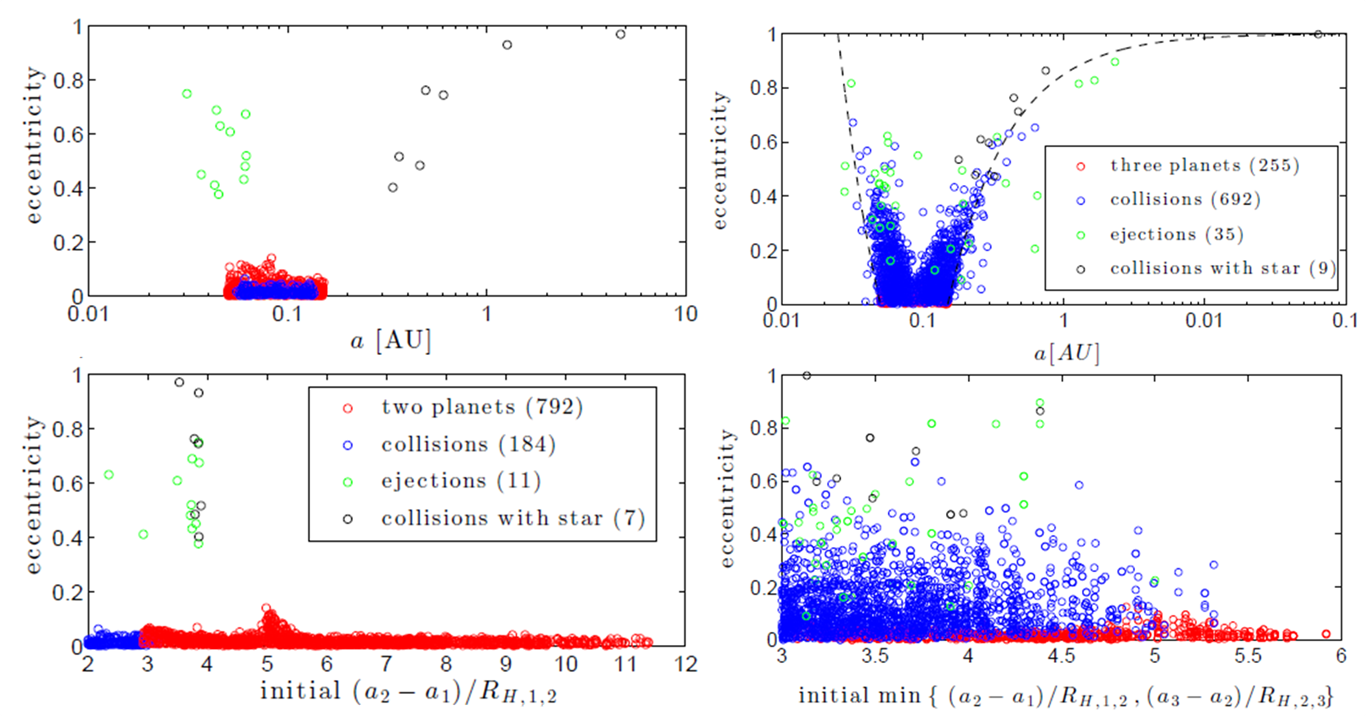
Figure 1. The results of the authors’ simulations showing that planet-planet scattering on small orbits cannot produce enough planets with high eccentricity. The left two panels are 2-planet simulations and the right two panels are 3-planet simulations. The top panels show the final eccentricity of the planet(s) versus the final semi-major axis, and the the bottom panel shows the final eccentricity versus the initial separation between the planets’ orbits (in units of their Hill radii). The points are color-coded by the outcome of the simulation — red are planets that all stayed in the system for the entire simulation, blue are the resulting planets created when the initial planets collided and merged, green are the planets that remained when the other was ejected from the system, and black are the planets that remained when the other collided with the star.
As you can see, most planets lasted for the entire simulation and stayed on fairly circular orbits. The second most likely outcome was planet-planet collision, which tends to create a new planet on a circular orbit. In only a few simulations did planets end up on eccentric orbits, and not nearly enough to match our observations.
The authors next performed a suite of simulations using three planets, and the results are shown in the right two panels in Figure 1. Collisions between planets were now the most common outcome, and the eccentricities of the resulting planets were somewhat higher than when only two planets were included, but overall the final eccentricities were still too small to match the observed exoplanet population. The mean eccentricity in this simulation was 0.096 compared with a mean of 0.19 in the observed population in this orbital range.
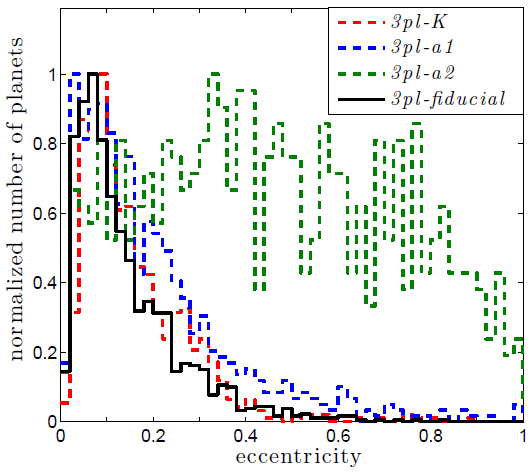
Figure 2. A histogram of the eccentricities at the end of the 3-planet simulations. The black line shows the results from close-in planets, while the green line shows the results from planets on larger orbits. Note that this figure only includes the results from the simulations in which something happened to the planets (collisions, ejections, etc.), in other words, the red points from Figure 1 are not included.
How could the simulations be changed to make the resulting orbits of the planets less circular? The authors tried a few variations, such as giving the planets different masses and changing their initial spacing, but the effects were negligible. The only way they could increase eccentricities was to put the planets on much larger orbits. These results are shown in Figure 2 in the form of a histogram of final eccentricities. The original 3-planet scenario (with orbits starting at 0.05-0.15 AU) is shown in black, compared with the new simulations with orbits starting at 2.5-7.5 AU in green. The wider orbit planets had a mean eccentricity of 0.31 and enough non-circular orbits to account for what we’ve observed.
The reason this works is as follows: A planet’s orbital velocity varies inversely with the size of its orbit, and the likelihood that a planet will collide with another planet — rather than be ejected from the system or thrown into the star — increases with orbital velocity. So planets on small orbits (which move more quickly) often collide and form a new planet on a circular orbit, while planets on large orbits (which move more slowly) are often ejected, leaving the other planet on an eccentric orbit.
But eccentric planets are observed on small orbits. We think these planets probably didn’t form on small orbits (because inside the snow-line there is an insignificant amount of solid material from which to form the core of a giant planet), so these planets probably migrated inwards at some point. This paper shows that if planet-planet scattering is the source of these planets’ non-circular orbits, then the scattering event must have occurred prior to the inward migration. Furthermore, the mechanism by which the planet migrates must preserve the eccentricity and not re-circularize the orbit (this is the meaning of “constraints on planet migration” in this paper’s title).
Of course, the eccentricity might not be a result of planet-planet scattering at all. Other theories to increase eccentricity involve planets interacting with their protoplanetary disk or distant companions initiating Kozai oscillations. It will take more exoplanet detections and more theoretical work like this paper before we can fully solve this puzzle.



Trackbacks/Pingbacks